A/B Test

What? A/B Test

---

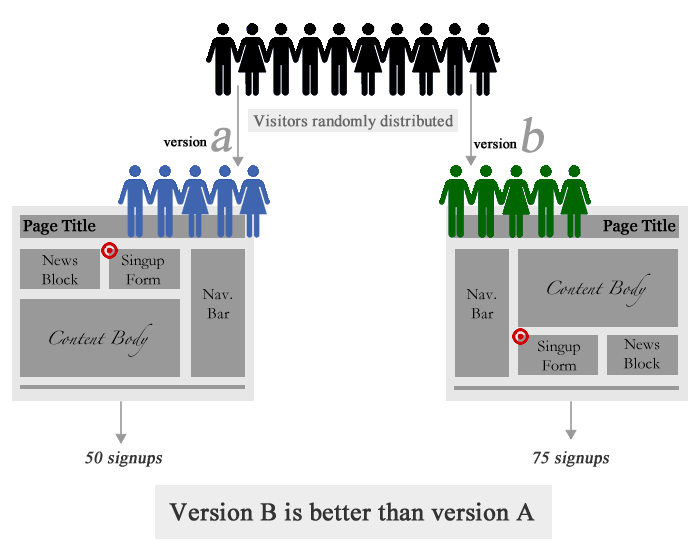
• A/B Test : 서로 다른 두 방법 간 효과의 차이를 밝히기 위한 대조 실험

  상관관계(Correlation) 를 파악하고자 하는 변수 $Y,X$ 외에 다른 요인들을 직접 통제할 수 없을 때 사용되는 통계적 디자인 패턴으로서, 임의로 나눈 두 집단에 대하여 서로 다른 방법을 적용하고 어떤 집단이 더 높은 성과를 보이는지 판단함. 이때 두 집단을 무작위로 추출함으로써, 두 집단이 제3의 요인들에 대하여 완전히 동질적일 수는 없지만 확률적으로 유사한 분포를 가지도록 함.

refer. Correlation VS. Causality

---

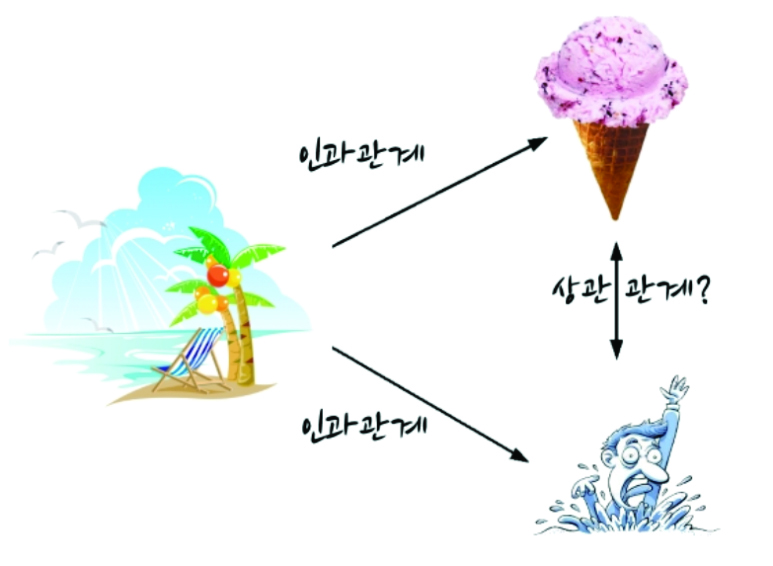
Example: 아이스크림 판매량과 물놀이 사고 간 관계성

한 지자체에서 물놀이 사고를 줄이는 것을 목표로 하고 있다. 조사 결과 아이스크림 판매량과 물놀이 사고 빈도 간의 상관관계가 높음을 알 수 있었다. 즉, 아이스크림 판매량이 증가하면 물놀이 사고가 증가하는 것이 데이터로부터 파악되었다. 이를 근거로 아이스크림 판매량 증가가 물놀이 사고 증가의 원인이라고 판단하였고, 물놀이 사고를 줄이기 위해 아이스크림 가격을 올려 판매량을 줄이는 정책을 입안하였다.

• 아이스크림 판매량과 물놀이 사고를 동시에 증가시키는 제3의 요인이 존재한다면?

Example: 웹사이트 디자인 개편과 매출 증가 간 관계성

어떤 쇼핑몰 웹 사이트에서 3개월에 걸쳐 디자인 개편 프로젝트를 진행하였고, 지난주에 성공적으로 새 디자인을 적용하였다. 그랬더니 갑자기 그 전에 비해 일 매출이 $10\%$ 증가했다. 매출 증가는 웹사이트 디자인 개편 덕분이라고 판단할 수 있는가?

• 새 디자인이 적용된 날 갑자기 경쟁 쇼핑몰이 문을 닫았다면?
• 새 디자인이 적용된 날 갑자기 인기 상품이 입고되었다면?
• 새 디자인이 적용된 날 갑자기 경기가 좋아졌다면?

Mean of a continuous random variable

---

문제	관심모수	점추정량	가정	검정가설	검정방법
단일 집단의 평균	$\mu$	$\bar{X}$	$n>30$	$H_0: \mu=\mu_0$	One Sample t-Test
두 집단 간 평균 비교 (독립표본)	$\mu_1-\mu_2$	\(\bar{X}_{1} - \bar{X}_{2}\)	$(n_1 + n_2)>30$	$H_0: \mu_1 - \mu_2 = 0$	Two Sample t-Test
두 집단 간 평균 비교 (쌍체표본)	$\mu_d$	$\bar{X}_d$	$n>30$	$H_0: \mu_d=0$	Paired Sample t-Test
셋 이상 그룹 간 평균 비교	$\mu_1, \cdots, \mu_m$	$\bar{X}_1, \cdots, \bar{X}_m$	$n_i>30$ $\sigma_{i}^{2}=\sigma_{j}^{2}$	$H_0: \mu_1 = \cdots = \mu_m$	ANOVA

Proportion of a discrete random variable

---

문제	관심모수	점추정량	가정	검정가설	검정방법
단일 집단의 비율	$\pi$	$p$	$np>5$ $n(1-p)>5$	$H_0: \pi=\pi_0$	One Sample z-Test
두 집단 간 비율 비교	$\pi_1 - \pi_2$	$p_1 - p_2$	$n_i p_i > 5$ $n_i (1-p_i)>5$	$H_0: \pi_1-\pi_2=0$	Two Sample z-Test
적합성 검정	$\pi_1, \cdots, \pi_m$	$p_1, \cdots, p_m$	$n_i p_i > 5$ $n_i (1-p_i)>5$	$H_0: \pi_1=p_{0}^{(1)}, \cdots, \pi_m=p_{0}^{(m)}$	Chi-square test
독립성 검정			$n_i p_i > 5$ $n_i (1-p_i)>5$	$H_0:$ 두 범주형 변수가 독립	Chi-square test

---

Sourse

• https://varify.io/en/blog/ab-testing/