Activation Functions

활성화 함수의 이해

---

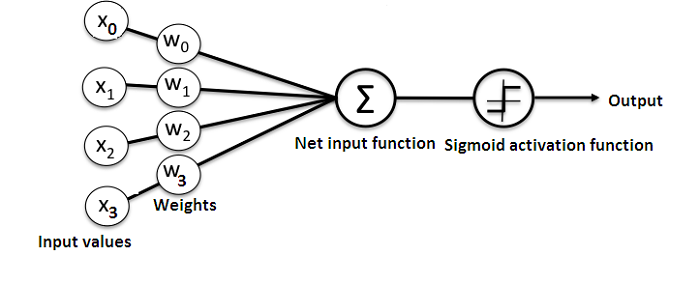
• 정의 : 순입력 함수 결과값에 대하여, 역치를 기준으로 정보 전달 여부를 판단하는 함수

  

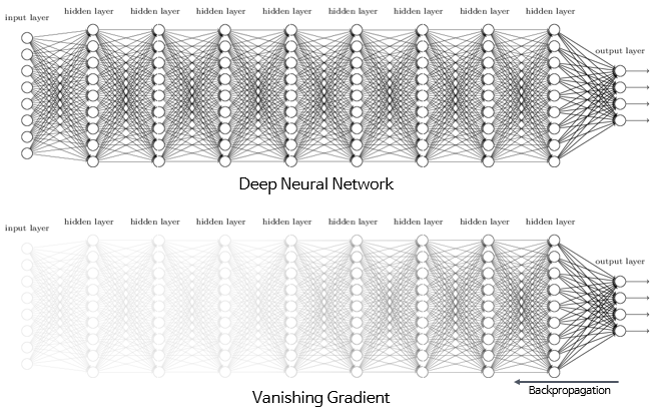
• 문제점

  • Hard Decision Problem

    

    • 현상 : 유의미하지 않은 차이로 인해 활성화 여부가 결정되는 현상

    • 원인 : 순전파 연산 과정에서 마진이 충분히 확보되지 않음

      • 마진(Margin) : 결정 경계와 가장 가까운 두 관측치 간 거리
      • 결정 경계(Decision Boundary) : 활성화 여부 판단 기준이 되는 선으로서 역치 혹은 임계값

  • Gradient Problem

    

    • 현상 : 역전파 학습 과정에서 출력층으로부터 멀어질수록 가중치가 제대로 갱신되지 않는 현상
    • 원인 : 활성화 함수의 도함수가 $0$ 과 $1$ 사이 값을 취함

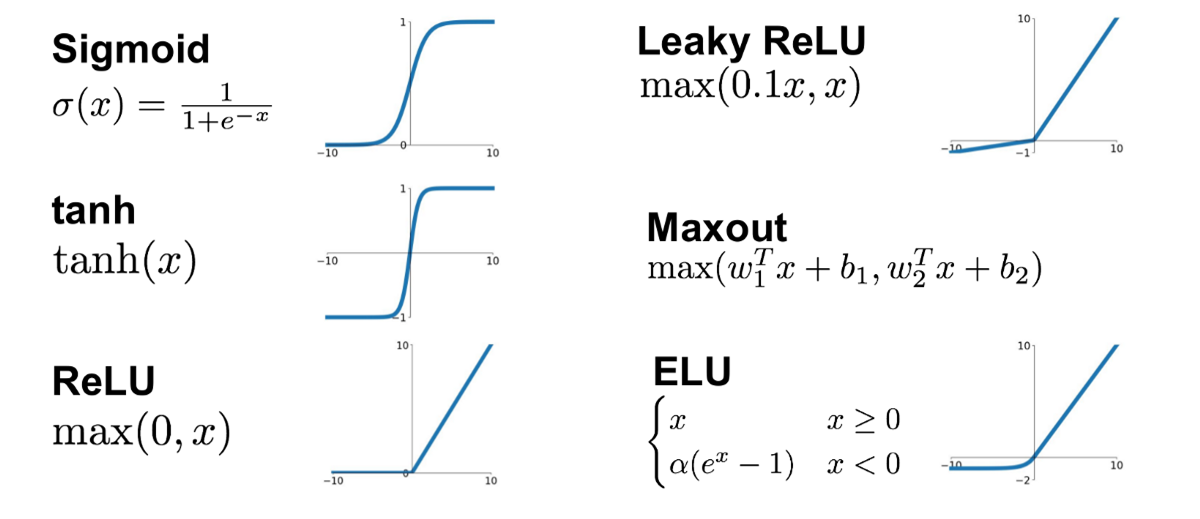
종류

---

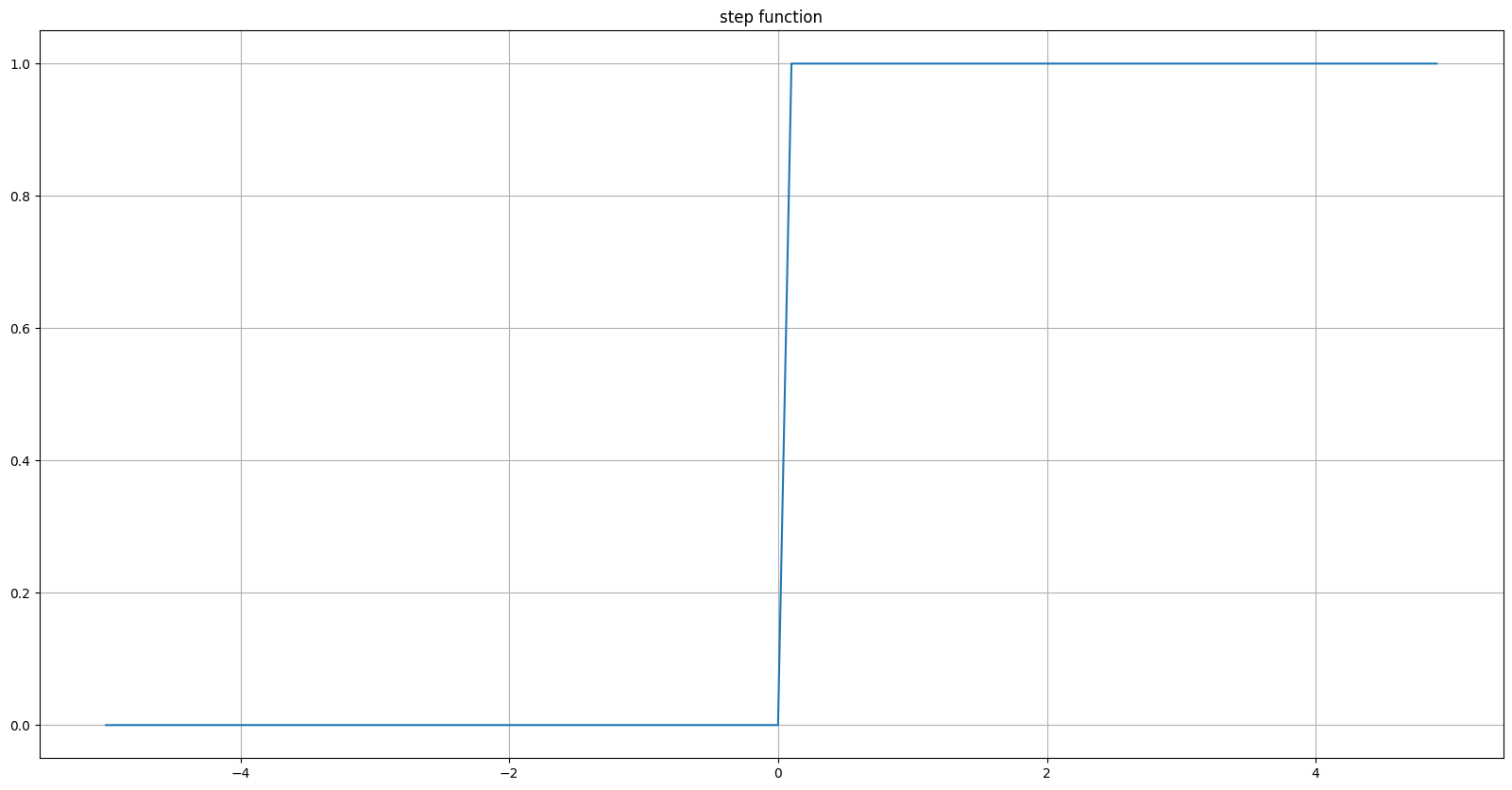
Step Function

• 공식

  \[\text{step}(x)=\begin{cases} 1, \ \text{if} \ x>0 \\ 0, \ \text{otherwise} \end{cases}\]

• 공역

  \[y \in \{0, 1\}\]

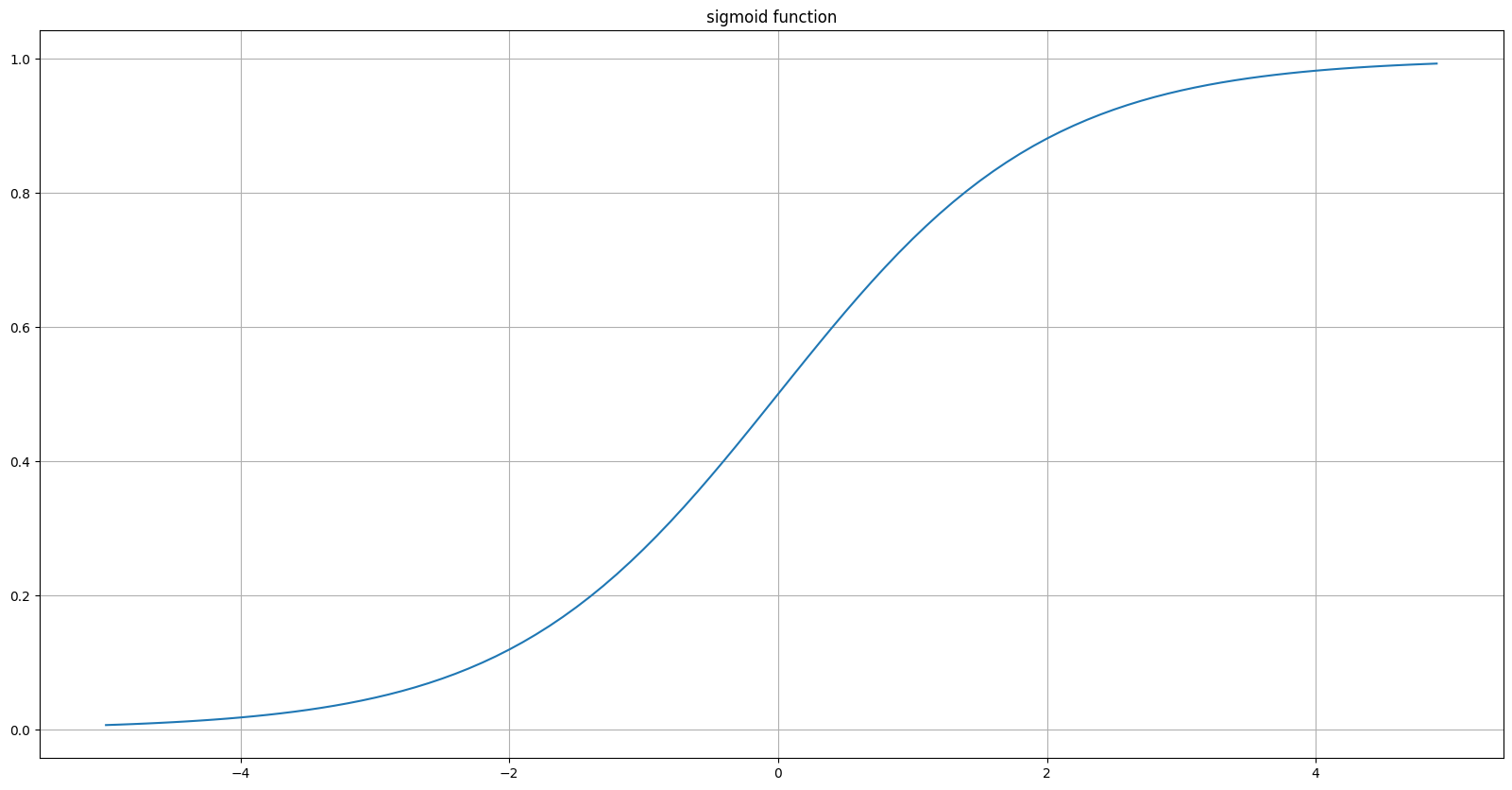
Sigmoid Function

• 공식

  \[\text{sigmoid}(x)=\frac{1}{1+e^{-x}}\]

• 공역

  \[y \in [0, 1]\]

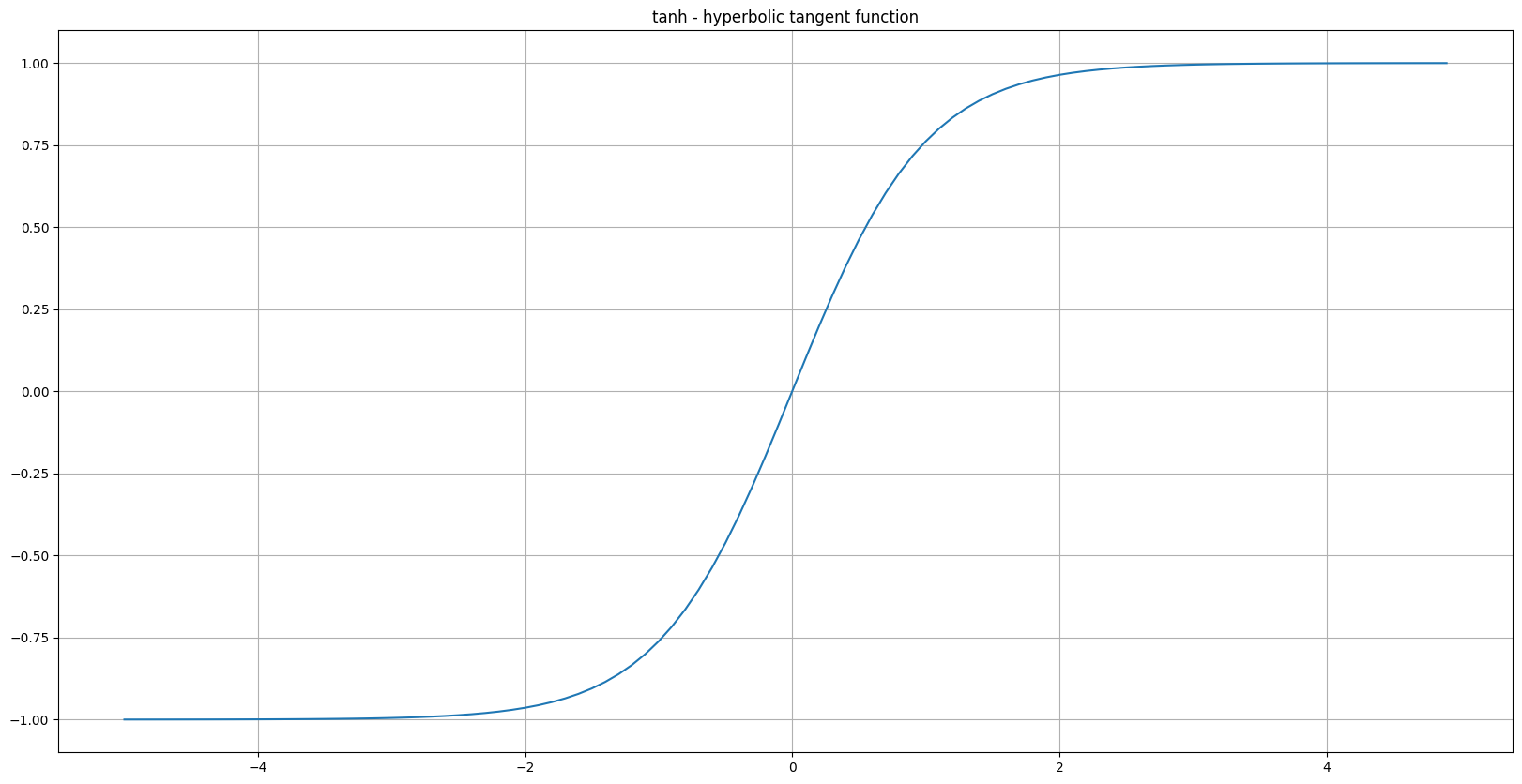
Hyperbolic TANgent(TANH) Function

• 공식

  \[\begin{aligned} \text{tanh}(x)&=\frac{\text{sinh}(x)}{\text{cosh}(x)} \\ &=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} \end{aligned}\]

• 공역

  \[y \in [-1, 1]\]

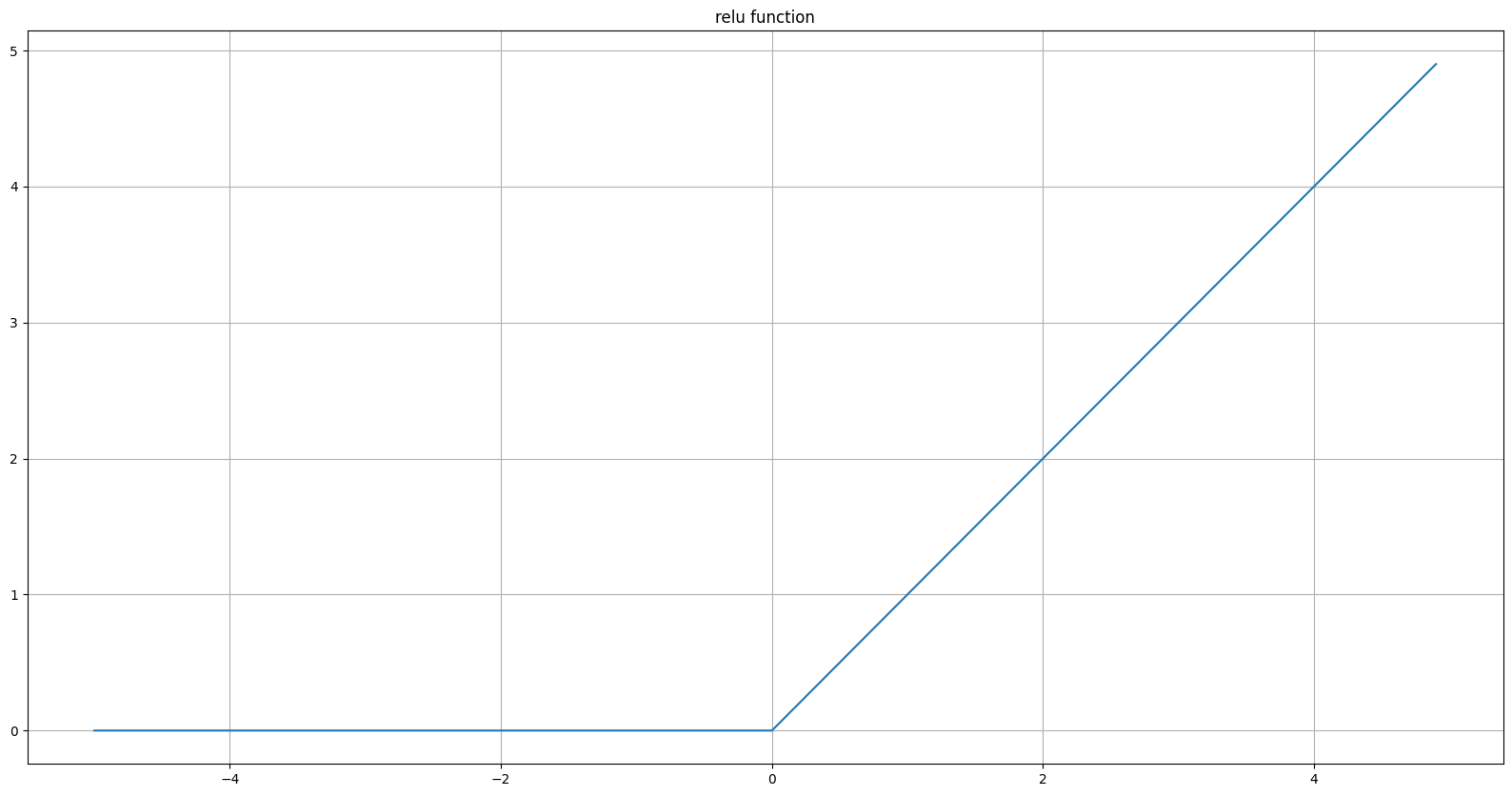
ReLU Function

• 공식

  \[\text{ReLU}(x)=\max(0,x)\]

• 공역

  \[y \in [0, \infty]\]

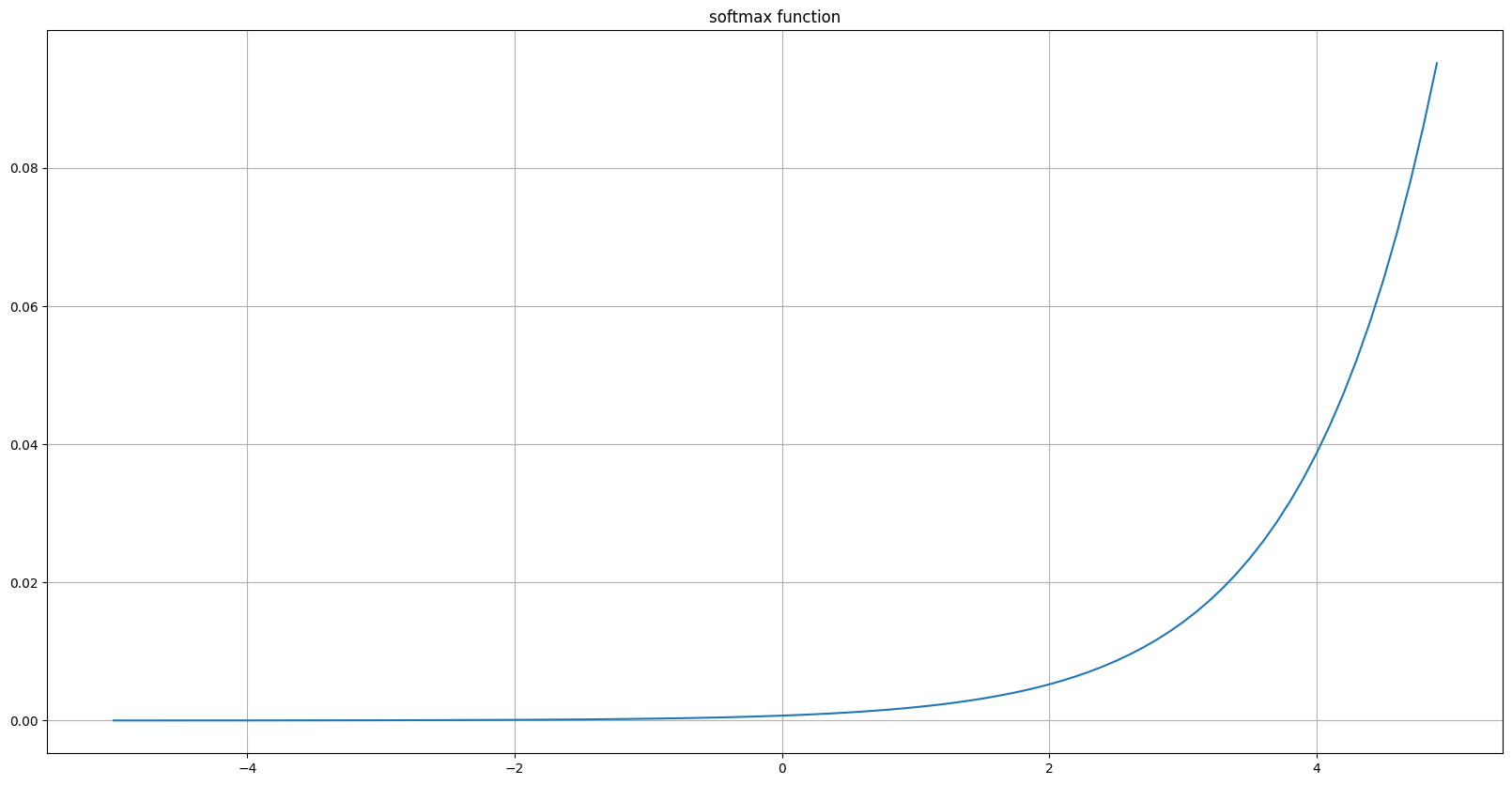
Softmax Function

• 공식

  \[\begin{aligned} \text{softmax}(x)_{i} &= \frac{e^{x_i}}{\textstyle \sum_{j \ne i}^{}{e^{x_j}}}\\ \displaystyle\sum_{i=1}^{n}{\text{softmax}(x)_{i}} &= 1\\ \text{softmax}(x) &= \Big\{\frac{e^{x_1}}{\textstyle \sum_{j \ne 1}^{}{e^{x_j}}}, \frac{e^{x_2}}{\textstyle \sum_{j \ne 2}^{}{e^{x_j}}}, \cdots , \frac{e^{x_i}}{\textstyle \sum_{j \ne i}^{}{e^{x_j}}}, \cdots , \frac{e^{x_n}}{\textstyle \sum_{j \ne n}^{}{e^{x_j}}}\Big\} \end{aligned}\]

• 공역

  \[y \in [0, 1]\]