AutoRec

AutoRec

---

• 문제 의식
  • RBM-CF(Restricted Boltzmann Machines for Collaborative Filtering): 확률적 생성 모형으로서, 평점값마다 별도의 파라미터를 설정하므로 학습 파라미터 수가 급증하고, 확률 생성 과정을 근사 학습하므로 수렴 속도가 느림
  • LLORMA(Local Low-Rank Matrix Approximation): 행렬분해 기반 잠재요인 모형으로서, 사용자 취향이 전역적으로 일관되지 않을 수 있다는 전제 하에 사용자-아이템 상호작용 행렬을 다수의 하위 행렬로 재구성하고, 각각을 지역적 저차원(Local Low Rank)으로 근사하나, 구조가 복잡함
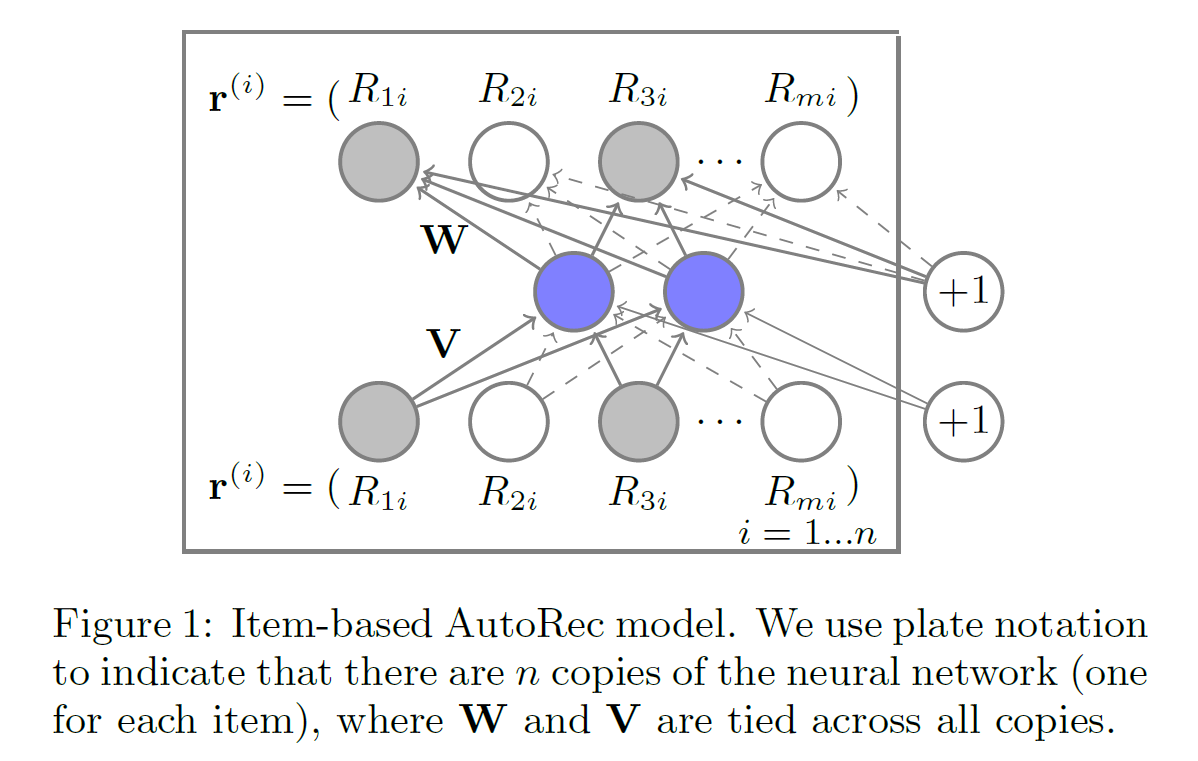
• AutoRec: 오토인코더 기반 협업필터링 모형으로서, 연속적 출력값을 결정론적 함수로 도출하는 단일 신경망 구조를 통해 선행 협업필터링 모형에 비해 계산 효율성과 구조적 간결성을 도모함
  • Sedhain, S., Menon, A. K., Sanner, S., & Xie, L.
    (2015, May).
    Autorec: Autoencoders meet collaborative filtering.
    In Proceedings of the 24th international conference on World Wide Web (pp. 111-112).

Notation

---

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\mathbf{R} \in \mathbb{R}^{M \times N}$: user-item explicit feedback matrix
• $\mathbf{V} \in \mathbb{R}^{M \times K}$: linear transformation matrix @ encoder
• $\mathbf{W} \in \mathbb{R}^{K \times M}$: linear transformation matrix @ decoder
• $\overrightarrow{\beta} \in \mathbb{R}^{K}$: bias vector @ encoder
• $\overrightarrow{\mathbf{b}} \in \mathbb{R}^{M}$: bias vector @ decoder
• $f(\cdot)$: activation function @ encoder
• $g(\cdot)$: activation function @ decoder

How to Modeling

---

• Prediction

  \[\begin{aligned} \hat{\mathbf{r}}_{i} &= g\left[\mathbf{W} \cdot f(\mathbf{V} \cdot \overrightarrow{\mathbf{r}}_{i} + \overrightarrow{\beta}) + \overrightarrow{\mathbf{b}} \right] \end{aligned}\]

  • Encoder(Dimensionality Reduction):

    \[\begin{aligned} \overrightarrow{\mathbf{z}}_{i} &= f(\mathbf{V} \cdot \overrightarrow{\mathbf{r}}_{i} + \overrightarrow{\beta}) \end{aligned}\]

  • Decoder(Reconstruction):

    \[\begin{aligned} \hat{\mathbf{r}}_{i} &= g(\mathbf{W} \cdot \overrightarrow{\mathbf{z}}_{i} + \overrightarrow{\mathbf{b}}) \end{aligned}\]

• Optimization

  \[\begin{aligned} \hat{\Theta} &= \text{arg} \min{\sum_{i=1}^{N}{\Vert \overrightarrow{\mathbf{r}}_{i} - h(\overrightarrow{\mathbf{r}}_{i} ; \Theta) \Vert_{\mathcal{O}}^{2}} + \frac{\lambda}{2}\Vert \Theta \Vert_{F}^{2}} \end{aligned}\]
  • \(h(\overrightarrow{\mathbf{r}}_{i} ; \Theta)\): Reconstruction Output
  • \(\Theta\): Learning Parameters
  • \(\Vert \cdot \Vert_{\mathcal{O}}^{2}\): L2 Loss Computed only for Observed Entries
  • \(\Vert \cdot \Vert_{F}^{2}\): Regularization Term