BPR

BPR

---

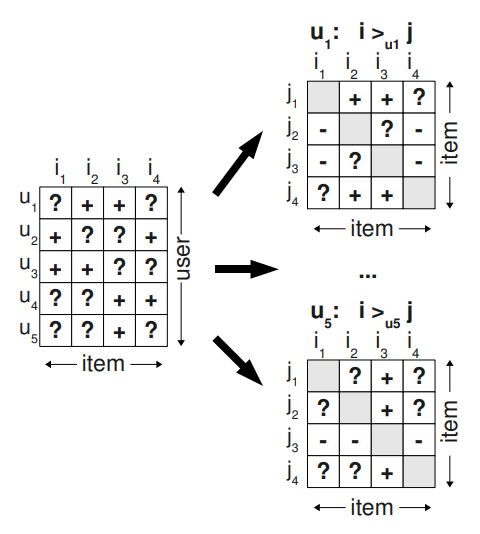
• BPR(Bayesian Personalized Ranking) : 베이지안 접근법을 활용한 개인화 순위 목적 함수

  선행 연구들은 대체로 평점 예측에 집중하는 경향을 보였으며, 이는 명시적 피드백 환경에 적합함. 하지만 실제에서는 주로 암묵적 피드백이 사용되며, 때문에 개별 아이템의 평점을 정확히 맞추는 것보다는 중요한 상호작용 정보과 중요하지 않은 상호작용 정보 간 차등을 두는 (아이템 간 선호 순위를 맞추는) 목적 함수가 요구됨.

Data Set

---

• 학습 데이터 : 개별 사용자 $u$ 의 선호체계 $>_{u}$

  • 비교 가능성(Totality)

    \[\forall i,j \in I:\quad i \ne j \quad \Rightarrow \quad \left(i >_{u} j\right) \vee \left(j >_{u} i\right)\]

  • 반대칭성(Anti-Symmetry)

    \[\forall i,j \in I:\quad \left(i >_{u} j\right) \wedge \left(j >_{u} i\right) \quad \Rightarrow \quad i = j\]

  • 이행성(Transitivity)

    \[\forall i,j,k \in I:\quad \left(i >_{u} j\right) \wedge \left(j >_{u} k\right) \quad \Rightarrow \quad \left(i >_{u} k\right)\]

• Pair-wise Preference Data Set

  \[\Omega = \Big\{(u,i,j) \mid i \in I_{u} \wedge j \in I \setminus I_{u}\Big\}\]
  • $I$ : 아이템 집합
  • $I_{u} \subset I$ : 사용자 $u$ 가 상호작용한 아이템 집합
  • $i \in I_{u}$ : 사용자 $u$ 가 상호작용한 아이템
  • $j \in I \setminus I_{u}$ : 사용자 $u$ 가 상호작용하지 아니한 아이템

• Single Data Point Definition

  \[x_{u,i,j}:=r_{u,i} - r_{u,j}\]

How to Modeling

---

Posterior Estimation

\[\underbrace{\ln{P(\Theta \mid \mathcal{D})}}_{\begin{array}{c} \text{Objective Function} \\ \text{(Log Posterior)} \end{array}} \propto \underbrace{\ln{P(\mathcal{D} \mid \Theta)}}_{\text{Log Likelihood}} + \underbrace{\ln{P(\Theta)}}_{\text{Log Prior}}\]

• Log Likelihood

  • Likelihood of Single Data Point

    \[\begin{aligned} P(i >_{u} j \mid \Theta) &= \sigma\left(\hat{x}_{u,i,j}\right) \end{aligned}\]

  • Likelihood of Data Set

    \[\begin{aligned} P(\mathcal{D} \mid \Theta) &= \prod_{(u,i,j)\in\Omega}{P(i >_{u} j \mid \Theta)}\\ &= \prod_{(u,i,j)\in\Omega}{\sigma\left(\hat{x}_{u,i,j}\right)} \end{aligned}\]

  • Log Likelihood

    \[\begin{aligned} \ln{P(\mathcal{D} \mid \Theta)} &= \ln{\prod_{(u,i,j)\in\Omega}{P(i >_{u} j \mid \Theta)}}\\ &= \sum_{(u,i,j)\in\Omega}{\ln{P(i >_{u} j \mid \Theta)}}\\ &= \sum_{(u,i,j)\in\Omega}{\ln{\sigma\left(\hat{x}_{u,i,j}\right)}} \end{aligned}\]

• Prior Determination; $\Theta \sim \mathcal{N}\left(0, \lambda_{\Theta}^{-1}\mathbf{I}\right)$

  \[\begin{aligned} P\left(\Theta\right) &= \frac{1}{(2\pi)^{d/2} \cdot \lambda_{\Theta}^{d/2}} \cdot \exp \left[-\frac{\lambda_{\Theta}}{2}\Vert \Theta \Vert^{2}\right]\\ \\ \ln{P\left(\Theta\right)} &= \ln{\frac{1}{(2\pi)^{d/2} \cdot \lambda_{\Theta}^{d/2}} \cdot \exp \left[-\frac{\lambda_{\Theta}}{2}\Vert \Theta \Vert^{2}\right]}\\ &= \ln{\frac{1}{(2\pi)^{d/2} \cdot \lambda_{\Theta}^{d/2}}} - \frac{\lambda_{\Theta}}{2}\Vert \Theta \Vert^{2}\\ &\propto -\lambda_{\Theta}\Vert\Theta\Vert^{2} \end{aligned}\]

• Posterior Estimation

  \[\begin{aligned} P(\Theta \mid \mathcal{D}) &\propto P(\mathcal{D} \mid \Theta) \cdot P(\Theta)\\ \\ \ln{P(\Theta \mid \mathcal{D})} &\propto \ln{P(\mathcal{D} \mid \Theta)} + \ln{P(\Theta)}\\ &\propto \sum_{(u,i,j)\in\Omega}{\ln{\sigma\left(\hat{x}_{u,i,j}\right)}} -\lambda_{\Theta}\Vert\Theta\Vert^{2} \end{aligned}\]

Optimization

• Objective Function

  \[\text{BPR-OPT} = \ln{P(\Theta \mid \mathcal{D})}\]

• Optimization

  \[\begin{aligned} \hat{\Theta} &= \text{arg} \max_{\Theta}{\ln{P(\Theta \mid \mathcal{D})}}\\ &= \text{arg} \max_{\Theta}{\sum_{(u,i,j)\in\Omega}{\ln{\sigma\left(\hat{x}_{u,i,j}\right)}} - \lambda_{\Theta}\Vert\Theta\Vert^{2}}\\ &= \text{arg} \min_{\Theta}{\sum_{(u,i,j)\in\Omega}{-\ln{\sigma\left(\hat{x}_{u,i,j}\right)}} + \lambda_{\Theta}\Vert\Theta\Vert^{2}} \end{aligned}\]
  • $\hat{\Theta}$ is MAP(Maximum a Posteriori) Estimator