Bayesian Framework

Causal Inference

---

• 역추리 문제(Inverse Inference Problem) : 다양한 원인 중 하나로부터 발생했음이 틀림없는 한 가지 사건이 발생했다고 가정하고, 그 원인들이 존재할 각각의 확률을 추리하는 문제(이영의, 2015, p.62)

  \[\begin{aligned} P(\text{cause} \mid \text{outcome}) = \frac{P(\text{cause} \wedge \text{outcome})}{P(\text{outcome})} = \frac{P(\text{outcome} \mid \text{cause}) \cdot P(\text{cause})}{P(\text{outcome})} \end{aligned}\]

  어떤 알려지지 않은 사건($Z$)이 발생하고($p$) 실패한 횟수($n-p$)가 주어졌을 때, 하나의 시행에서 그 사건이 발생할 확률($\theta$)이 지정될 수 있는 두 가지 확률($\alpha, \beta$) 사이에 있을 기회가 요청된다($\alpha < \theta < \beta$). (Bayes, 1763, p.376)

  베이즈 정리는 주어진 환경에서 하나의 사건($Z$)에 대해 동일한 환경에서 그것이 어떤 횟수만큼 발생했고($p$) 어떤 다른 횟수만큼 발생하는 데 실패했다는 것을($n-p$) 제외한 그 밖의 것에 대해 아무 것도 알지 못한다는 가정에서($\theta \sim \text{Uniform}$) 해당 사건이 발생할 확률($\theta$)을 판단할 방법을 찾는 일이다. (Price, 1763, 서문)

• 직접 확률(Direct Probability; $P(B \mid A)$) : 시행의 성질이 먼저 규정되고($P(A)$) 이어서 시행에서($P(B \mid A)$) 하나 또는 그 이상의 가능한 결과가 발생할 확률($P(A \wedge B)$) (이영의, 2015, p.62)

  \[\begin{aligned} P(B \mid A) &= \frac{P(A \wedge B)}{P(A)} \end{aligned}\]

• 역확률(Inverse Probability; $P(A \mid B)$) : 이미 시행의 결과가 제시되고($P(B)$) 그 다음 실제로 실행된 시행이($P(B \mid A)$) 가능한 시행 중($P(B)=\int{P(B \mid A) \cdot P(A)\text{d}A}$) 특정 시행에 해당할 확률($P(A \wedge B)$) (이영의, 2015, p.62)

  \[\begin{aligned} P(A \mid B) &= \frac{P(A \wedge B)}{P(B)} \end{aligned}\]

Bayes’ Billiard Table Analogy

---

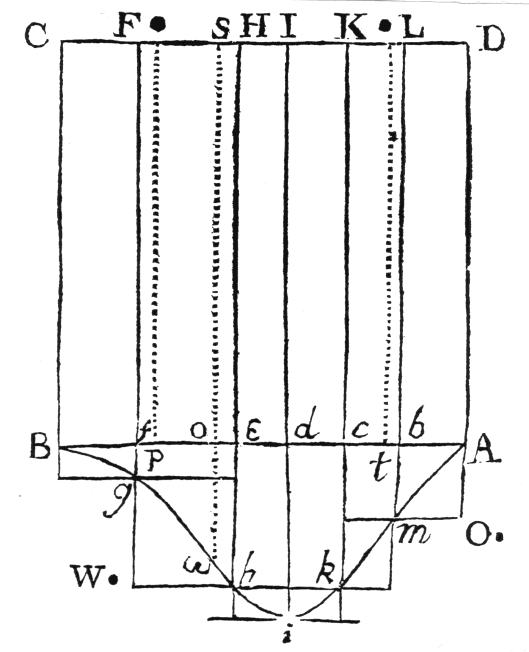
당구대 $ABCD$ 를 가정하자. 공 $\mathcal{W}, \mathcal{O}$ 가 그 위에 굴려지면 어떤 하나의 동일한 부분에 정지할 동일한 확률을 가진다. $\mathcal{W}$ 으로 선분 $OS$ 의 위치가 결정된다. 그 우측 또는 좌측에 $\mathcal{O}$ 이 정지하는가에 따라서 사건 $Z$ 의 발생 또는 실패가 결정된다. $\mathcal{O}$ 를 연속하여 $n$ 회 던진 결과 $p$ 회만큼 우측에 정지했음이 관찰되었다. 이때 $AD$ 와 $OS$ 사이의 미지의 거리 $\theta$ 가 두 가지 값 $\alpha, \beta$ 사잇값을 취할 확률은?

• 공 $\mathcal{W}$ 가 던져지기 이전에 $\theta$ 가 $\alpha, \beta$ 사이에 있고,
  사건 $Z$ 가 $n$ 번의 시행에서 $p$ 번 발생하고 $n-p$ 번 실패할 확률:

  \[\begin{aligned} P(\alpha < \theta < \beta, X=p) &= \int_{\alpha}^{\beta}{\binom{n}{p} \theta^{p}(1-\theta)^{n-p}\text{d}\theta} \end{aligned}\]

• 사건 $Z$ 가 $p$ 번 발생할 확률:

  \[\begin{aligned} P(X=p) &= P(0 < \theta < 1, X=p)\\ &= \int_{0}^{1}{\binom{n}{p} \theta^{p}(1-\theta)^{n-p}\text{d}\theta} \end{aligned}\]

• $\theta$ 의 값에 대해 어느 것도 알려지기 이전에($0<\theta<1$),
  사건 $Z$ 가 $n$ 번의 시행에서 $p$ 번 발생하고 $n-p$ 번 실패한 것으로 드러날 때,
  그로부터 $\theta$ 가 $\alpha, \beta$ 사이에 있다고 추측한다면,
  그 추측이 옳을 확률:

  \[\begin{aligned} P(\alpha < \theta < \beta \mid X=p) &= \frac{P(\alpha < \theta < \beta, X=p)}{P(0 < \theta < 1, X=p)}\\ &= \frac{\int_{\alpha}^{\beta}{\cancel{\binom{n}{p}} \theta^{p}(1-\theta)^{n-p}\text{d}\theta}}{\int_{0}^{1}{\cancel{\binom{n}{p}} \theta^{p}(1-\theta)^{n-p}\text{d}\theta}}\\ &= \frac{\int_{\alpha}^{\beta}{\theta^{p}(1-\theta)^{n-p}\text{d}\theta}}{\int_{0}^{1}{\theta^{p}(1-\theta)^{n-p}\text{d}\theta}} \end{aligned}\]

Scholum

내가 $Z$ 라고 불렀던 그러한 사건의 경우에, 일정 횟수로 시행하고($n$) 그것이 발생하고($p$) 실패한 횟수($n-p$)를 통해, 그것에 대해서는 다른 어떤 것도 알지 못한 상태에서 그것의 확률에 관해 추측할 수 있고(Non-Informative Prior of $\theta$), 언급한 면적들의 크기를 계산하는 일반적인 방법에 의해 그러한 추측이 옳을 기회를 알 수 있다(Posterior of $\theta \mid \mathcal{D}$).

그리고 동일한 규칙이 그것에 관해 이루어진 어떤 시행에서도, 우리가 사전에 전혀 알지 못하는 확률을 갖는 사건의 경우에도 사용될 수 있다는 것은 다음을 생각해보면 나타난 것 같다. 즉, 어떤 횟수의 시행에서 그것이 다른 횟수보다 어떤 가능한 다른 횟수로 발생할 것이라는 점을 생각할 이유가 없다.

그러므로 나는 다음부터 당연히 사건 $Z$ 에 대해 주어진 규칙($\theta$)이 또한 어떠한 시행이 이루어지거나 관찰되기 전에(Prior) 어떤 것도 알려지지 않은(Non-Informative) 사건의 확률(Posterior of $\theta \mid \mathcal{D}$)에도 이용될 수 있다고 간주할 것이다. 나는 그러한 사건을 알려지지 않은 사건(Non-Informative Prior)이라고 부를 것이다. (Bayes, 1763, p.393)

Bayesian Framework

---

• 베이지안 프레임워크(Bayesian Framework): 데이터 관측 이전의 사전 신념(Prior Belief)을 바탕으로, 데이터 관측 이후의 사후 신념(Posterior Belief)을 갱신함으로써 시행의 성질(모수)이 확정적이지 않은 상태에서 그 성질에 대하여 추론하는 방법론

  \[\begin{aligned} \underbrace{P\left(\Theta \mid \mathcal{D} \right)}_{\text{Posterior}} = \underbrace{\frac{P\left(\mathcal{D} \cap \Theta\right)}{P\left(\mathcal{D}\right)}}_{\begin{array}{c} \text{Conditional}\\ \text{Probability} \end{array}} = \frac{\overbrace{P\left(\mathcal{D} \mid \Theta \right)}^{\text{Likelihood}} \cdot \overbrace{P\left(\Theta\right)}^{\text{Prior}}}{\underbrace{P\left(\mathcal{D}\right)}_{\text{Evidence}}} \end{aligned}\]

• 사후 확률 분포(Posterior Probability Distribution): 모수에 대한 인식적 불확실성으로서, 단일 사건에 대한 다수 진술의 신뢰도 집합을 나타냄

  \[\begin{aligned} P\left(\Theta \mid \mathcal{D} \right) \end{aligned}\]
  • 시행의 성질에 관한 믿음(Posterior)은 관측 가능한 대상이 아니므로 직접적으로 구할 수 없음
  • 베이즈 정리는 이 믿음(Posterior)을 직접 확률(Likelihood)과 사전 정보(Prior)의 조합으로써 간접적으로 도출함

• 우도(Likelihood): 데이터에 대한 모수의 상대적 적합성으로서, 데이터 생성 과정상의 무작위성으로 인한 우발적 불확실성을 반영함

  \[\begin{aligned} P\left(\mathcal{D} \mid \Theta \right) \end{aligned}\]

• 사전 확률 분포(Prior Probability Distribution): 모수에 대한 사전 정보

  \[\begin{aligned} P\left(\Theta\right) \end{aligned}\]

• 증거(Evidence): 데이터가 관찰될 확률로서, 모수에 대한 신념을 뒷받침하는 증거로 해석됨

  \[\begin{aligned} P\left(\mathcal{D}\right) &= \int{P(\mathcal{D} \mid \Theta) \cdot P(\Theta)\text{d}\Theta} \end{aligned}\]

  베이지안에서는 모수에 대하여 주장함에 있어 현재 주어진 정보, 가령 사전 정보, 데이터 관측 결과 등을 기반으로 함. 따라서 현재까지 관찰된 데이터가 실현될 가능성은 모수에 대한 주장의 증거(Evidence)임.

[example] 동전 던지기

---

동전을 던졌을 때 앞면이 나올 확률을 $\theta$ 라고 하자. $\theta$ 에 대한 정보가 아무것도 없다고 가정하자. 즉, $\theta$ 는 0과 1 사이의 무작위수일 것이라고 믿어지고 있다. 동전을 두 번 던졌는데 두 번 다 앞면이 나왔다. 그렇다면 $\theta$ 에 대한 믿음은 어떻게 변화할까?

• Prior Prob. Dist.:

  \[\begin{aligned} p(\theta) =1 \quad \because \theta \sim \text{Uniform}(0,1) \end{aligned}\]

• Likelihood:

  \[\begin{aligned} p\left(X \mid \theta\right) =\frac{n!}{X!(n-X)!} \cdot \theta^{X} \cdot (1-\theta)^{n-X} \quad \because X \mid \theta \sim \text{Bin}(n,\theta) \end{aligned}\]

• Evidence:

  \[\begin{aligned} p(X) &= \int_{0}^{1}{p\left(X \mid \theta\right)}\text{d}\theta\\ &= \int_{0}^{1}{\frac{n!}{X!(n-X)!} \cdot \theta^{X} \cdot (1-\theta)^{n-X}}\text{d}\theta\\ &= \frac{n!}{X!(n-X)!} \cdot \int_{0}^{1}{\theta^{X} \cdot (1-\theta)^{n-X}}\text{d}\theta\\ &= \frac{n!}{X!(n-X)!} \cdot \text{B}(X+1,n-X+1)\\ &= \frac{n!}{X!(n-X)!} \cdot \frac{\Gamma(X+1)\Gamma(n-X+1)}{\Gamma(n+2)} \quad \because (X+1),(n-X+1) \in \mathbb{R}^{+}\\ &= \frac{n!}{X!(n-X)!} \cdot \frac{X!(n-X)!}{(n+1)!} \quad \because (X+1),(n-X+1) \in \mathbb{Z}^{+}\\ &= \frac{1}{n+1} \end{aligned}\]

• Posterior Prob. Dist.:

  \[\begin{aligned} p\left(\theta \mid X\right) &\propto p\left(X \mid \theta\right) \cdot p\left(\theta\right)\\ &= \frac{n!}{X!(n-X)!} \cdot \theta^{X} \cdot (1-\theta)^{n-X}\\ \\ \therefore \theta \mid X &\sim \text{Beta}(X+1,n-X+1) \end{aligned}\]

  • $\text{Beta}(\alpha,\beta)$ : 베타분포

    \[f(x) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{\text{B}(\alpha,\beta)} \sim \text{Beta}(\alpha,\beta)\]

Annotation

• $\text{B}(\alpha,\beta)$ : 베타 함수

  \[\begin{aligned} \text{B}(\alpha,\beta) &= \int_{0}^{1}{t^{\alpha-1}(1-t)^{\beta-1}}\text{d}t\\ &= \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)} \quad \text{where}\; \alpha,\beta \in \mathbb{R}^{+} \end{aligned}\]

• $\Gamma(n)$ : 감마 함수

  \[\begin{aligned} \Gamma(n) &= \int_{0}^{\infty}{t^{(n-1)}e^{-t}}\text{d}t\\ &= (n-1)! \quad \text{where}\; n \in \mathbb{Z}^{+} \end{aligned}\]

• $\text{Beta}(\alpha,\beta)$ : 베타분포

  \[f(x) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{\text{B}(\alpha,\beta)} \sim \text{Beta}(\alpha,\beta)\]

---

Reference

• 베이즈주의; 합리성으로부터 객관성으로의 여정
  이영의. (2015). 한국연구재단 저술총서 4. 한국문화사