Bernoulli and Extension

Bernoulli

---

• 베르누이 분포(Bernoulli Distribution): $p$ 의 확률로 성공 여부가 결정되는 단일 시행(베르누이 시행)에서 성공 여부를 나타내는 분포

  \[X\sim\mathrm{Bernoulli}(\pi),\quad X\in\{0,1\}\]
  • $0<\pi<1$: 성공 가능성으로서 확률 파라미터

• probability mass function:

  \[p(X=k\mid \pi) =\pi^{k}(1-\pi)^{1-k}\]

• moment generating function:

  \[\begin{aligned} M_{X}(t) &=\mathbb{E}_{p(x)}\left[\exp{tX}\right]\\ &=\pi\cdot\exp{[t-1]}+(1-\pi)\cdot\exp{[t-0]}\\ &=\pi\cdot\exp{t}+(1-\pi) \end{aligned}\]
  • $\mathbb{E}\left[X\right]=(\mathrm{d}/\mathrm{d}t)M_{X}(t)\vert_{t=0}=\pi$
  • $\mathbb{E}\left[X^{2}\right]=(\mathrm{d}^{2}/\mathrm{d}t^{2})M_{X}(t)\vert_{t=0}=\pi$
  • $\mathrm{Var}\left[X\right]=\mathbb{E}\left[X^{2}\right]-\mathbb{E}\left[X\right]^{2}=\pi(1-\pi)$

• canonical form:

  \[\begin{aligned} p(x) &=\pi^{x}(1-\pi)^{1-x}\\ &=\exp{\left[x\log{\pi}+(1-\pi)\log{(1-\pi)}\right]}\\ &=1\cdot\exp{\left[x\cdot\log{\frac{\pi}{1-\pi}}+\log{(1-\pi)}\right]} \end{aligned}\]
  • $T(x)=x$
  • $\eta(\theta)=\log{\left[\pi/(1-\pi)\right]}$
  • $A(\eta)=-\log{(1-\pi)}$
  • $h(x)=1$

conjugate prior

---

• bernoulli model:

  \[X\mid\pi\sim\mathrm{Bernoulli}(\pi)\]

• canonical form:

  \[p(x\mid\pi) =1\cdot\exp{\left[x\cdot\log{\frac{\pi}{1-\pi}}+\log{(1-\pi)}\right]}\]
  • $T(x)=x$
  • $\eta(\theta)=\log{\left[\pi/(1-\pi)\right]}$
  • $A(\eta)=-\log{(1-\pi)}$
  • $h(x)=1$

• prior of $\eta$:

  \[\begin{aligned} p(\pi) &\propto\exp{\left[\alpha\cdot\eta(\theta)-\beta\cdot A(\eta)\right]}\\ &=\exp{\left[\alpha\cdot\eta-\beta\cdot\log{\left(1+\exp{\eta}\right)}\right]}\\ &=\exp{\alpha\eta}\cdot\left(1+\exp{\eta}\right)^{-\beta} \end{aligned}\]

• change of variables $\eta\to\pi$:

  \[\begin{aligned} p_{\pi}(\pi)\mathrm{d}\pi &=p_{\eta}(\eta)\mathrm{d}\eta\\ \therefore p_{\pi}(\pi) &=p_{\eta}\left(\log{\frac{\pi}{1-\pi}}\right)\left\vert\frac{\mathrm{d}\eta}{\mathrm{d}\pi}\right\vert\\ &\propto\exp{\left[\alpha\cdot\log{\frac{\pi}{1-\pi}}\right]}\left(1+\exp{\left[\log{\frac{\pi}{1-\pi}}\right]}\right)^{-\beta}\cdot\frac{1}{\pi(1-\pi)}\\ &=\pi^{\alpha}(1-\pi)^{-\alpha}\cdot(1-\pi)^{\beta}\cdot\pi^{-1}(1-\pi)^{-1}\\ &=\pi^{\alpha-1}(1-\pi)^{(\beta-\alpha)-1}\\ &=\mathrm{Beta}(\alpha,\beta-\alpha) \end{aligned}\]

• Therefore, the success probability of the Bernoulli distribution $\pi$ follows a Beta distribution. Here, each parameter of the Beta distribution represents (1) Amount of Success Data and (2) Amount of Failure Data.

  \[\pi\sim\mathrm{Beta}(\alpha,\beta)\]

Binomial

---

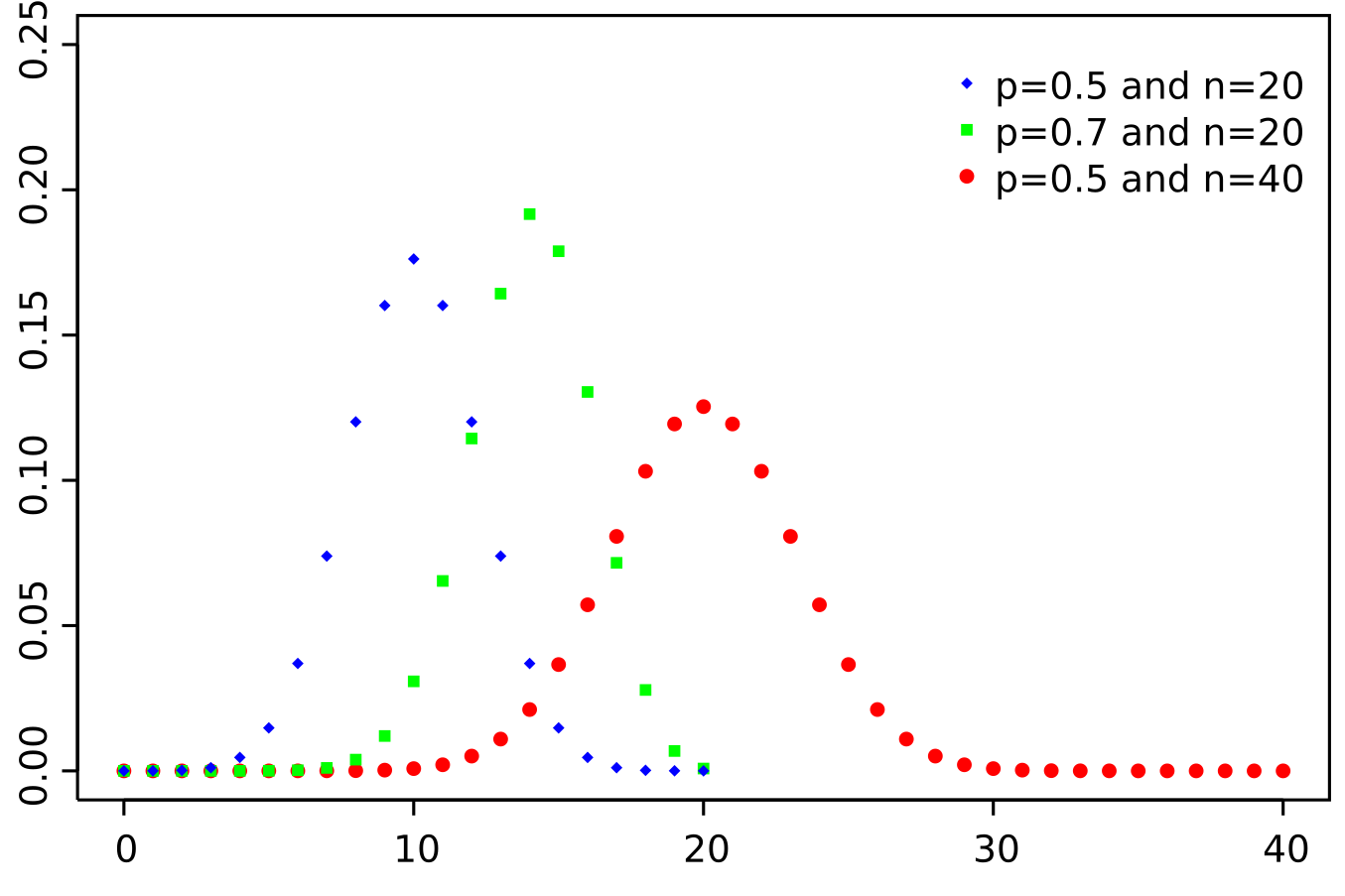
• 이항 분포(Binomial Distribution): 베르누이 분포의 실행 횟수를 일반화한 분포로서, $n$ 번의 베르누이 시행에서 성공 횟수를 나타내는 분포

  \[\begin{gathered} X:=\sum_{i=1}^{n}{Z_{i}},\quad Z_{i}\overset{\mathrm{i.i.d}}{\sim}\mathrm{Bernoulli}(\pi)\\ \Downarrow\\ X\sim\mathrm{Binomial}(n,\pi) \end{gathered}\]
  • $n$: 베르누이 시행 횟수
  • $0<\pi<1$: 성공 가능성으로서 확률 파라미터

• probability mass function:

  \[p(X=k\mid \pi) =\begin{pmatrix}n\\x\end{pmatrix}\pi^{k}(1-\pi)^{n-k}\]

• 조합(Combination):

  \[_{n}C_{k} :=\begin{pmatrix}n\\ k\end{pmatrix} =\frac{n!}{k!(n-k)!}\]

• moment generating function:

  \[\begin{aligned} M_{X}(t) &=\mathbb{E}_{p(x)}\left[\exp{tX}\right]\\ &=\mathbb{E}_{p(x)}\left[\exp{\left(t\cdot\sum_{i=1}^{n}{Z_{i}}\right)}\right]\\ &=\mathbb{E}_{p(x)}\left[\exp{\sum_{i=1}^{n}{tZ_{i}}}\right]\\ &=\mathbb{E}_{p(x)}\left[\prod_{i=1}^{n}{\exp{tZ_{i}}}\right]\\ &=\prod_{i=1}^{n}{\mathbb{E}_{p(x)}\left[\exp{tZ_{i}}\right]}\quad(\because Z_{i}\perp Z_{j})\\ &=\left[\pi\cdot\exp{t}+(1-\pi)\right]^{n} \end{aligned}\]
  • $\mathbb{E}\left[X\right]=(\mathrm{d}/\mathrm{d}t)M_{X}(t)\vert_{t=0}=\pi$
  • $\mathbb{E}\left[X^{2}\right]=(\mathrm{d}^{2}/\mathrm{d}t^{2})M_{X}(t)\vert_{t=0}=n\pi+n(n-1)\pi^{2}$
  • $\mathrm{Var}\left[X\right]=\mathbb{E}\left[X^{2}\right]-\mathbb{E}\left[X\right]^{2}=n\pi(1-\pi)$

• canonical form:

  \[\begin{aligned} p(x) &=\begin{pmatrix}n\\x\end{pmatrix}\pi^{x}(1-\pi)^{n-x}\\ &=\begin{pmatrix}n\\x\end{pmatrix}\exp{\left[x\cdot\log{\pi}+(n-x)\cdot\log{(1-\pi)}\right]}\\ &=\begin{pmatrix}n\\x\end{pmatrix}\cdot\exp{\left[x\cdot\log{\frac{\pi}{1-\pi}}+n\cdot\log{(1-\pi)}\right]} \end{aligned}\]
  • $T(x)=x$
  • $\eta(\theta)=\log{\left[\pi/(1-\pi)\right]}$
  • $A(\eta)=-n\cdot\log{(1-\pi)}$
  • $h(x)=\begin{pmatrix}n\ x\end{pmatrix}$