CDAE

CDAE

---

• 문제 의식: AutoRec 의 한계점
  • Implicit Feedback Problem
    • 구조적 편향 문제(Structural Bias): 관측과 미관측이 특정한 선택 경로와 제약 조건 하에서 발생했다는 점을 간과하고 선호와 비선호로 이분하는 데서 오는 체계적 왜곡
    • 클래스 불균형 문제(Class Imbalance): AutoRec 은 명시적 피드백 데이터 하에서 관측만을 사용하여 최적화를 수행하나, 암시적 피드백 데이터 하에서 이는 모든 상호작용을 $1$ 로 예측하는 문제를 야기함
  • Personalization Problem: AutoRec 은 행렬 복원에 초점을 맞추어 최적화를 수행하므로 히스토리는 유사하나 잠재적 선호 구조(latent preference structure)는 다른 사용자들 간에 제공되는 추천의 개인화가 미흡할 수 있음
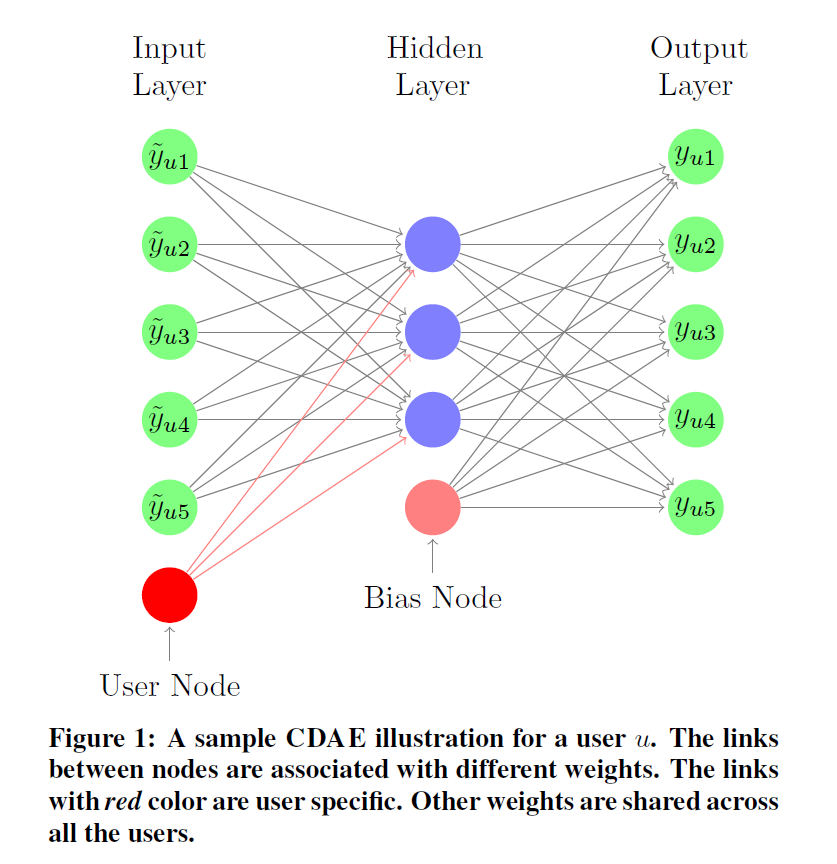
• CDAE(Collaborative Denoising AutoEncoder): 잡음을 활용하여 암시적 피드백 데이터 하에서 손상된 선호도를 복원하고, 사용자 잠재 벡터를 활용하여 개인화 성능 향상을 꾀하는 오토인코더 기반 협업필터링 모형
  • Wu, Y., DuBois, C., Zheng, A. X., & Ester, M.
    (2016, February).
    Collaborative denoising auto-encoders for top-n recommender systems.
    In Proceedings of the ninth ACM international conference on web search and data mining (pp. 153-162).

Notation

---

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\mathbf{Y} \in \mathbb{R}^{M \times N}$: user-item implicit feedback matrix
• $\mathbf{X} \in \mathbb{R}^{M \times N}$: masked $\mathbf{Y}$
• $\mathbf{M} \in \mathbb{R}^{M \times N}$: masking matrix
• $\overrightarrow{\mathbf{u}}_{u} \in \mathbb{R}^{K}$: user latent factor vector
• $\mathbf{V} \in \mathbb{R}^{M \times K}$: linear transformation matrix @ encoder
• $\mathbf{W} \in \mathbb{R}^{K \times M}$: linear transformation matrix @ decoder
• $\overrightarrow{\beta} \in \mathbb{R}^{K}$: bias vector @ encoder
• $\overrightarrow{\mathbf{b}} \in \mathbb{R}^{M}$: bias vector @ decoder
• $f(\cdot)$: activation function @ encoder
• $g(\cdot)$: activation function @ decoder

How to Modeling

---

• Generate Masking Noise

  \[\begin{aligned} \overrightarrow{\mathbf{x}}_{u} &= \overrightarrow{\mathbf{y}}_{u} \odot \overrightarrow{\mathbf{m}}_{u}, \quad \overrightarrow{\mathbf{m}}_{u} \sim \text{Bernouli}(1-p)^{N} \end{aligned}\]
  • \(\overrightarrow{\mathbf{m}}_{u} \sim \text{Bernouli}(1-p)^{N}\): \(m_{u,i} \sim \text{Bernouli}(1-p)\) independently

• Prediction

  \[\begin{aligned} \hat{\mathbf{y}}_{u} &= g\left[\mathbf{W} \cdot f(\mathbf{V} \cdot \overrightarrow{\mathbf{x}}_{u} + \overrightarrow{\mathbf{u}}_{u} + \overrightarrow{\beta}) + \overrightarrow{\mathbf{b}} \right] \end{aligned}\]

  • Encoder(Dimensionality Reduction):

    \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u} &= f(\mathbf{V} \cdot \overrightarrow{\mathbf{x}}_{u} + \overrightarrow{\mathbf{u}}_{u} + \overrightarrow{\beta}) \end{aligned}\]

  • Decoder(Reconstruction):

    \[\begin{aligned} \hat{\mathbf{y}}_{u} &= g(\mathbf{W} \cdot \overrightarrow{\mathbf{z}}_{u} + \overrightarrow{\mathbf{b}}) \end{aligned}\]

• Optimization

  \[\begin{aligned} \Theta &= \text{arg} \min{\frac{1}{M}\sum_{u=1}^{M}{\mathbb{E}_{\mathbf{X} \sim P(\cdot \mid \mathbf{Y})}[\mathcal{L}(\mathbf{y}_{u}, \hat{\mathbf{y}}_{u})] + \frac{\lambda}{2} \Vert \Theta \Vert_{F}^{2}}} \end{aligned}\]
  • \(\mathcal{L}(\mathbf{y}_{u}, \hat{\mathbf{y}}_{u})\): Reconstruction Loss
  • \(\mathbb{E}_{\mathbf{X} \sim P(\cdot \mid \mathbf{Y})}\): Average Loss because of Stochasticity of Noise
  • \(\Theta\): Learning Parameters
  • \(\Vert \cdot \Vert_{F}^{2}\): Regularization Term