Collaborative Filtering

Collaborative Filtering

---

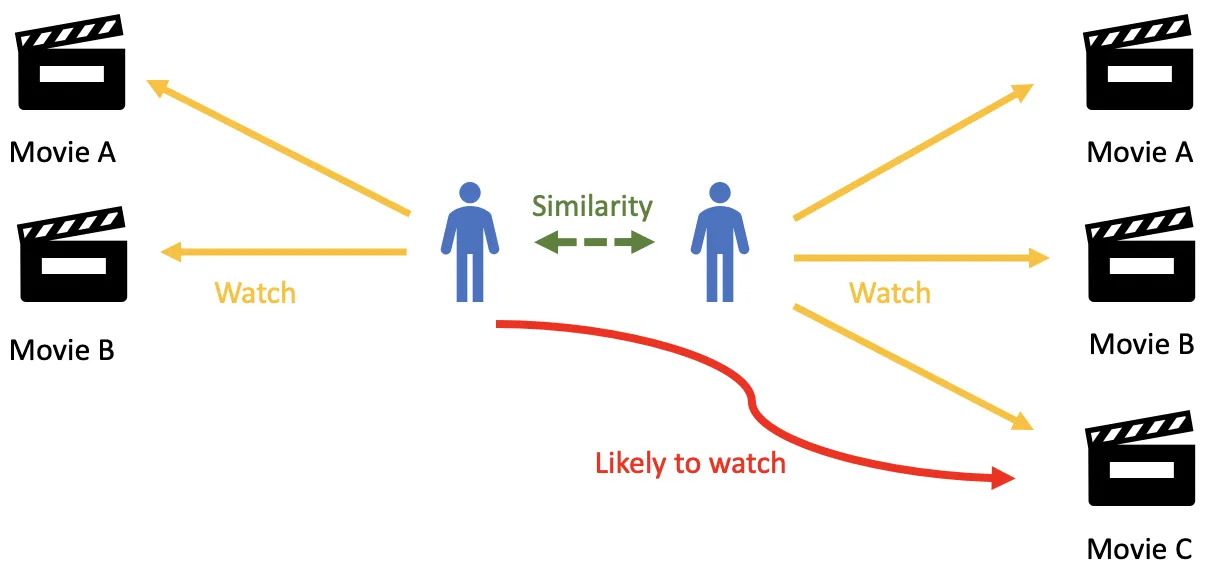
• 협업 필터링(Collaborative Filtering): 과거 여러 사용자들이 다양한 아이템에 대하여 평가 점수를 매긴 기록을 활용하여 아직 상호작용하지 않은 아이템에 대한 사용자의 평점을 추론하는 방법론

  

  • 사용자 기반 협업 필터링(User-Based Collaborative Filtering): Identify like-minded users
  • 아이템 기반 협업 필터링(Item-Based Collaborative Filtering): Identify buying patterns

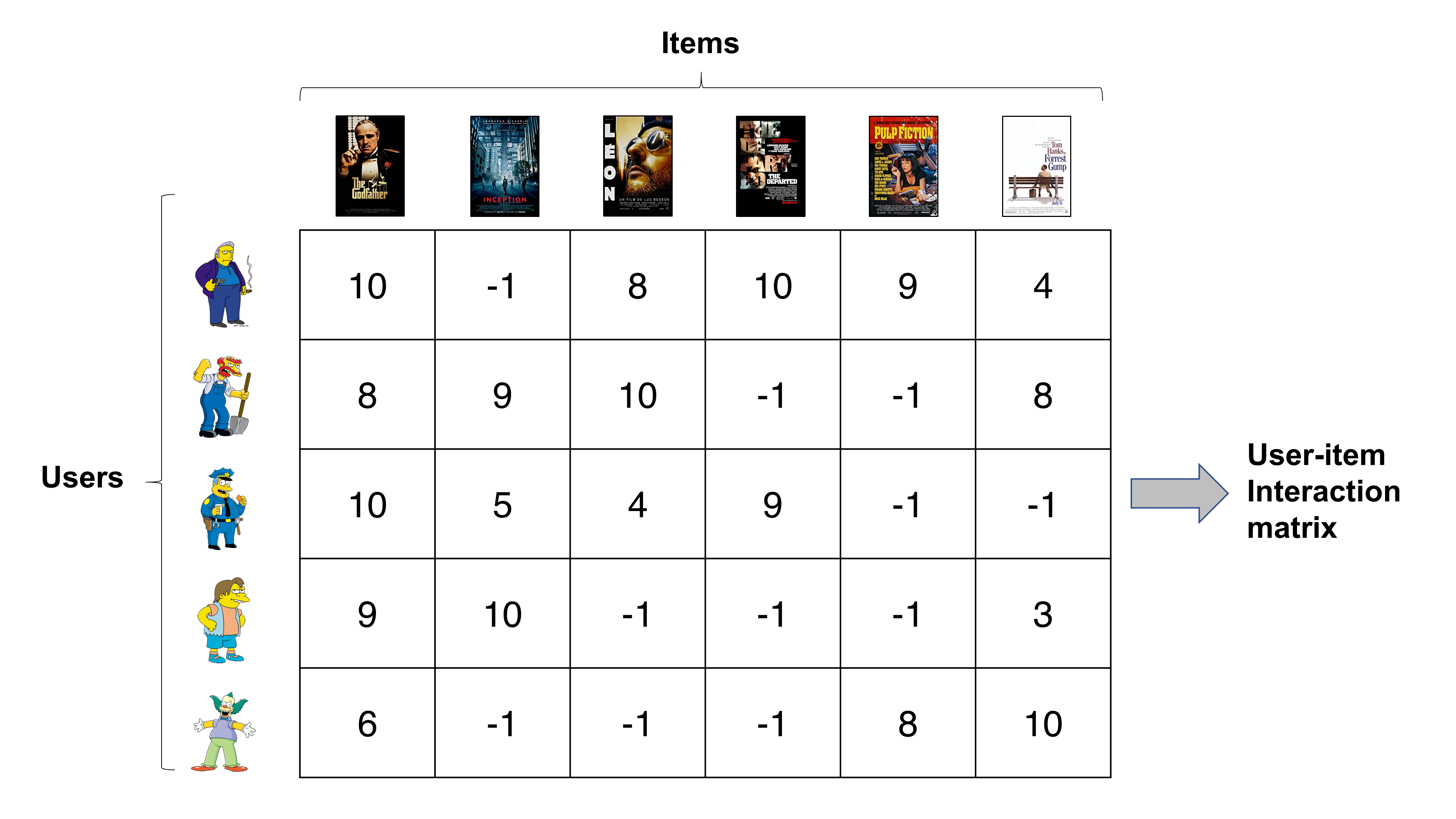
• 사용자-아이템 상호작용 행렬(User-Item Interaction Matrix): $M$ 명의 사용자와 $N$ 가지 아이템 간의 상호작용을 수치적으로 표현한 행렬로서, 통상 행 벡터는 사용자를, 열 벡터는 아이템을 의미함

  

  \[r_{u,i} \in \mathbf{R} \in \mathbb{R}^{M \times N}\]
  • 협업 필터링은 실질적으로 사용자-아이템 상호작용 행렬의 결측치(위 예시의 $-1$)를 채우는 방법이므로 행렬 완성 문제라고도 부름

Function

---

• Bias-aware Collaborative Filtering Function

  \[\begin{aligned} \hat{r}_{u,i} &= \mu + \beta_{u} + \beta_{i} + \text{what} \end{aligned}\]
  • $\hat{r}_{u,i}$: 사용자 $u$ 의 아이템 $i$ 에 대한 평점 예측값
  • $\mu$: 커뮤니티 평점 평균
  • $\beta_{u}$: 사용자 $u$ 의 평균 평점 편차로서 사용자의 평점 척도
  • $\beta_{i}$: 아이템 $i$ 의 평균 평점 편차로서 아이템의 인기도

• What?

  • k-NN Algorithm(Memory based Collaborative Filtering)
  • Matrix Factorization Algorithm(Latent Factor Model)

Memory based Collaborative Filtering

---

• 메모리 기반 협업 필터링(Memory based Collaborative Filtering): (사용자 기반 협업 필터링 기준으로) 사용자가 상호작용하지 않은 아이템에 대한 선호를 예측함에 있어, 해당 아이템에 대한 피어 그룹의 선호를 유사도만큼 가중 평균하는 방법

  \[\begin{aligned} \text{what} &= \frac{\sum_{v \in p(i \mid u)}{\text{sim}(u,v) \cdot \left(r_{v,i}-\overline{r}_{v}\right)}}{\sum_{v \in p(i \mid u)}{\vert \text{sim}(u,v) \vert}} \end{aligned}\]
  • $v \in p(i \mid u)$ : 타깃 사용자 $u$ 의 $k$-Nearest Neighbor 중 타깃 아이템 $i$ 에 대하여 펑점을 매긴 사용자 집합으로서 피어 그룹(Peer Group)

How to Calculate $\text{sim}(u,v)$

• 피어슨 상관계수(Pearson Correlation Coefficient): 사용자 벡터 간 평점 척도에 차이가 클 경우 유용함

  \[\begin{aligned} \text{sim}(u,v) &= \frac{\sum_{j \in I_{u} \cap I_{v}}{\left(r_{u,j}-\overline{r}_{u}\right)\cdot\left(r_{v,j}-\overline{r}_{v}\right)}}{\sqrt{\sum_{j \in I_{u} \cap I_{v}}{\left(r_{u,j}-\overline{r}_{u}\right)^{2}}}\cdot\sqrt{\sum_{j \in I_{u} \cap I_{v}}{\left(r_{v,j}-\overline{r}_{v}\right)^{2}}}} \end{aligned}\]

• 코사인 유사도(Cosine Measure): 상호작용 데이터가 희박할 경우 유용함

  \[\begin{aligned} \text{sim}(u,v) &= \frac{\overrightarrow{\mathbf{r}}_{u} \cdot \overrightarrow{\mathbf{r}}_{v}}{\Vert \overrightarrow{\mathbf{r}}_{u} \Vert_{L2} \cdot \Vert \overrightarrow{\mathbf{r}}_{v} \Vert_{L2}} \end{aligned}\]
  • \(\overrightarrow{\mathbf{r}}_{u} \in \mathbf{R}_{M \times N}\) : 사용자-아이템 상호작용 행렬의 행 벡터로서 사용자 벡터

Discount Methods

• 유사도 할인(Discounted Similarity): 두 사용자 간 공동으로 상호작용한 아이템 갯수($\vert I_{u} \cap I_{v}\vert$)가 적을 경우, 유사도 값을 신뢰하기 어려우므로 이에 비례하여 유사도를 할인함

  \[\begin{aligned} \text{sim}(u,v) &\leftarrow \underbrace{\frac{\min{\Big(\vert I_{u} \cap I_{v}\vert, \beta\Big)}}{\beta}}_{\text{Discount Factor}} \cdot \text{sim}(u,v) \end{aligned}\]

• 중요도 할인(Discounted Importance): 대중성 있는 아이템의 경우 사용자가 이미 경험했거나 인지하고 있지만 소비하지 아니하기로 결정한 아이템일 가능성이 높으므로, 대중성에 비례하여 아이템의 중요도(평점)을 할인함

  \[\begin{aligned} \overrightarrow{\mathbf{r}}_{i} &\leftarrow \underbrace{\log{\frac{M}{m_{i}}}}_{\text{Discount Factor}} \cdot \overrightarrow{\mathbf{r}}_{i} \end{aligned}\]
  • \(\overrightarrow{\mathbf{r}}_{i} \in \mathbf{R}_{M \times N}\): 사용자-아이템 상호작용 행렬의 열 벡터로서 아이템 벡터
  • $M$: 총 사용자 수
  • $m_{i}$: 아이템 $i$ 에 대하여 상호작용한 사용자 수

Latent Factor Model

---

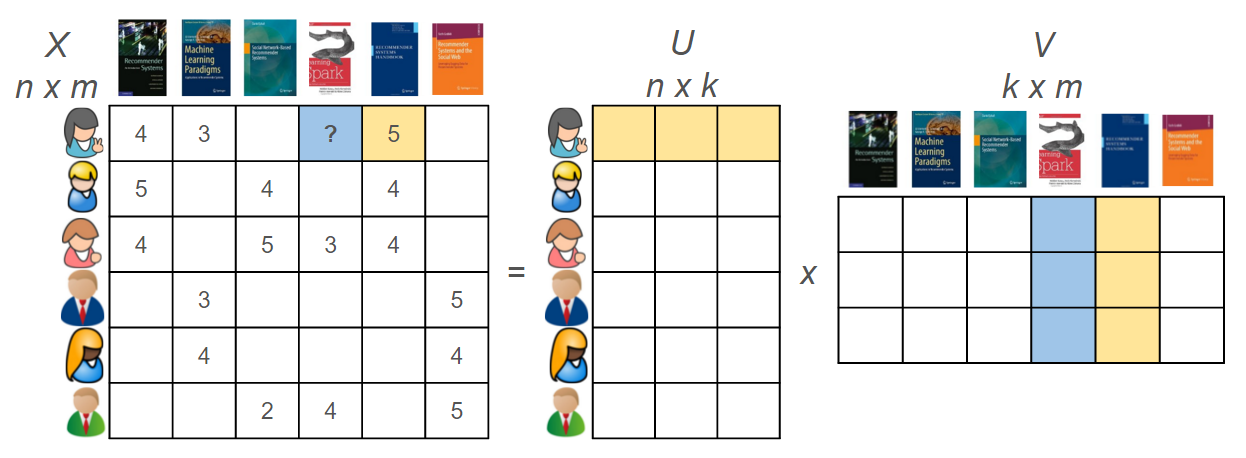
• 잠재요인 모형(Latent Factor Model) : 사용자 벡터와 아이템 벡터를 정체를 알 수 없는 $k$ 개의 특징 공간으로 사상하는 방법

  

  협업 필터링에서 사용자는 아이템들에 대한 평점 집합으로(Row vector of the user-item interaction matrix), 아이템은 사용자들로부터 받은 평점 집합으로(Column vector of the user-item interaction matrix) 표현됨. 이처럼 사용자와 아이템은 각각 서로를 표현하는 벡터 공간 축이 되므로 직접 비교할 수 없음. 잠재요인 모형은 공통된 표현 수단인 잠재요인을 가정함으로써 이 문제를 해결함.

MF

• Matrix Factorization: Original Latent Factor Model

  \[\begin{aligned} \text{what} &= \overrightarrow{\mathbf{p}}_{u} \cdot \overrightarrow{\mathbf{q}}_{i} \end{aligned}\]
  • \(\overrightarrow{\mathbf{p}}_{u} \in \mathbf{P}_{M \times K}\): 사용자-잠재요인 벡터로서, 사용자 $u$ 의 선호 정보로 해석됨
  • \(\overrightarrow{\mathbf{q}}_{i} \in \mathbf{Q}_{N \times K}\): 아이템-잠재요인 벡터로서, 아이템 $i$ 의 특징 정보로 해석됨

• SVD++ : 특정 사용자가 특정 아이템에 대하여 매길 평점을 추론함에 있어, 목표 아이템 외에 사용자가 상호작용했던 다른 아이템들의 잠재요인 정보들을 함께 고려하는 방법

  \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u} \leftarrow \overrightarrow{\mathbf{p}}_{u} + \frac{\sum_{j \in R(u)}{\overrightarrow{\mathbf{q}}_{j}}}{\sqrt{\vert R(u)\vert}} \end{aligned}\]
  • \(\displaystyle\frac{\sum_{j \in R(u)}{\overrightarrow{\mathbf{q}}_{j}}}{\sqrt{\vert R(u)\vert}}\): 사용자 $u$ 가 상호작용한 아이템 벡터의 평균으로서, $u$ 가 상호작용한 아이템들의 평균적인 특성
  • $R(u)$: 사용자 $u$ 가 상호작용한 아이템 집합

Optimization

• Objective Function for Bias-unaware Matrix Factorization

  \[\begin{aligned} \hat{\overrightarrow{\mathbf{p}}}_{u}, \hat{\overrightarrow{\mathbf{q}}}_{i} &= \text{arg} \min_{\Theta}{\mathcal{J}\left(r_{u,i},\hat{r}_{u,i}\right) + \lambda_{\Theta}\Vert \Theta \Vert^{2}} \end{aligned}\]

• 교대최소제곱법(Alternating Least Square; ALS): $\mathbf{P},\mathbf{Q}$ 에 대하여 한 번에 하나의 행렬을 고정한 상태에서 다른 행렬을 최적화하는 과정을 번갈아 반복하여 수렴시키는 최적화 알고리즘으로서, 최소자승법을 활용하므로 각 사용자의 상호작용 데이터를 독립적으로 연산할 수 있어 병렬 처리에 적합함

• Objective Function:

  \[\begin{aligned} \hat{\overrightarrow{\mathbf{p}}}_{u} &= \text{arg} \min_{\mathbf{p}}{\Vert \overrightarrow{\mathbf{r}}_{u} - \mathbf{Q} \cdot \overrightarrow{\mathbf{p}}_{u}\Vert^{2} + \lambda \Vert \overrightarrow{\mathbf{p}}_{u} \Vert^{2}}, \quad \text{where Q is fixed}\\ \hat{\overrightarrow{\mathbf{q}}}_{i} &= \text{arg} \min_{\mathbf{q}}{\Vert \overrightarrow{\mathbf{r}}_{i} - \mathbf{P} \cdot \overrightarrow{\mathbf{q}}_{i}\Vert^{2} + \lambda \Vert \overrightarrow{\mathbf{q}}_{i} \Vert^{2}}, \quad \text{where P is fixed} \end{aligned}\]

• Optimality Condition:

  \[\begin{aligned} \frac{\partial L}{\partial \overrightarrow{\mathbf{p}}_{u}} &= -2\mathbf{Q}^{T} \cdot \left(\overrightarrow{\mathbf{r}}_{u} - \mathbf{Q} \cdot \overrightarrow{\mathbf{p}}_{u}\right) + 2\lambda \cdot \overrightarrow{\mathbf{p}}_{u} = 0\\ \frac{\partial L}{\partial \overrightarrow{\mathbf{q}}_{i}} &= -2\mathbf{P}^{T} \cdot \left(\overrightarrow{\mathbf{r}}_{i} - \mathbf{P} \cdot \overrightarrow{\mathbf{q}}_{i}\right) + 2\lambda \cdot \overrightarrow{\mathbf{q}}_{i} = 0 \end{aligned}\]

• Optimality Params:

  \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u} &\leftarrow \left(\mathbf{Q}^{T}\mathbf{Q} + \lambda \mathbf{I}\right)^{-1}\mathbf{Q}^{T}\overrightarrow{\mathbf{r}}_{u}\\ \overrightarrow{\mathbf{q}}_{i} &\leftarrow \left(\mathbf{P}^{T}\mathbf{P} + \lambda \mathbf{I}\right)^{-1}\mathbf{P}^{T}\overrightarrow{\mathbf{r}}_{i} \end{aligned}\]

---

Source

• https://towardsdatascience.com/essentials-of-recommendation-engines-content-based-and-collaborative-filtering-31521c964922
• https://buomsoo-kim.github.io/recommender%20systems/2020/09/25/Recommender-systems-collab-filtering-12.md/