Convolutional Neural Networks

Why? Conv-Net

---

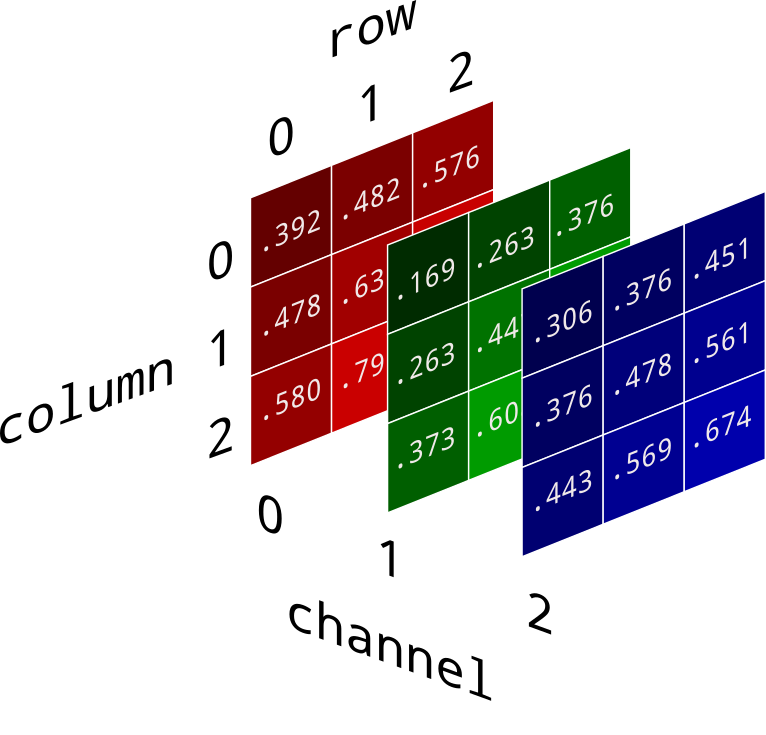
• image data is spatially structured data:

  

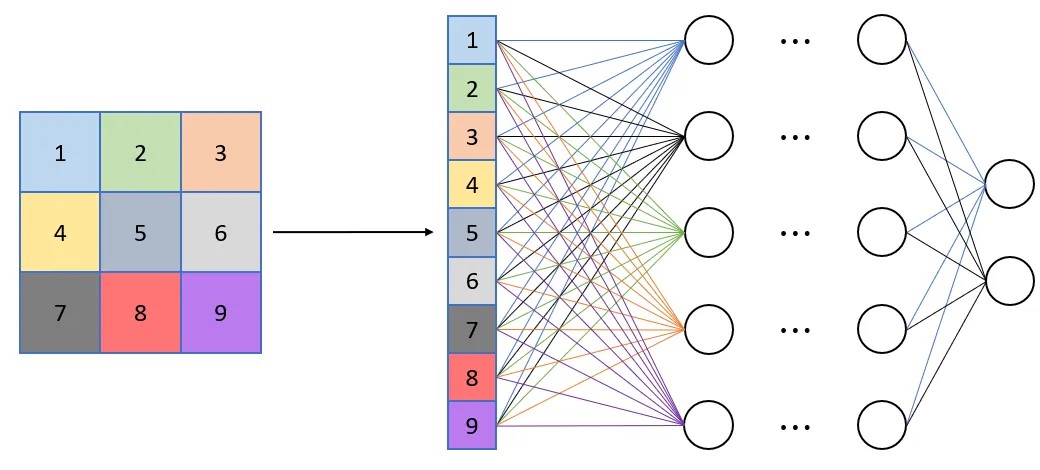
• fully connected layers flatten the dimensionality of the input,
  collapsing its spatial structure:

  

• CNN(Convolutional Neural Networks) involves preprocessing operations
  that preserve spatial structure:

  

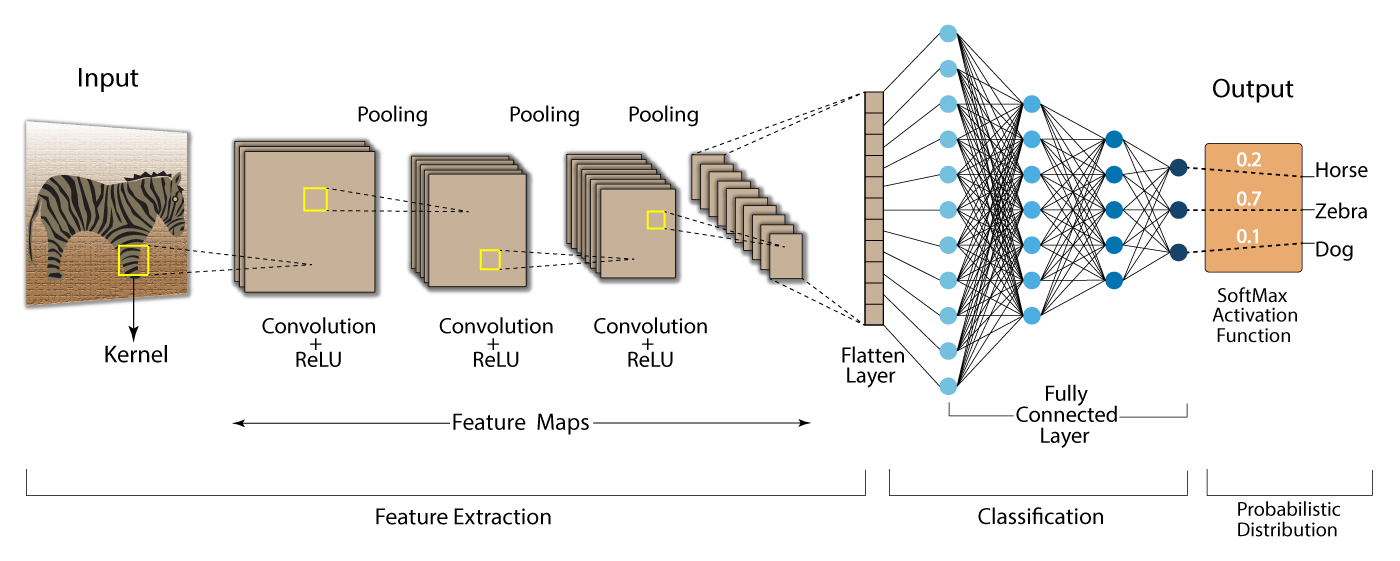
How to Extract Features

---

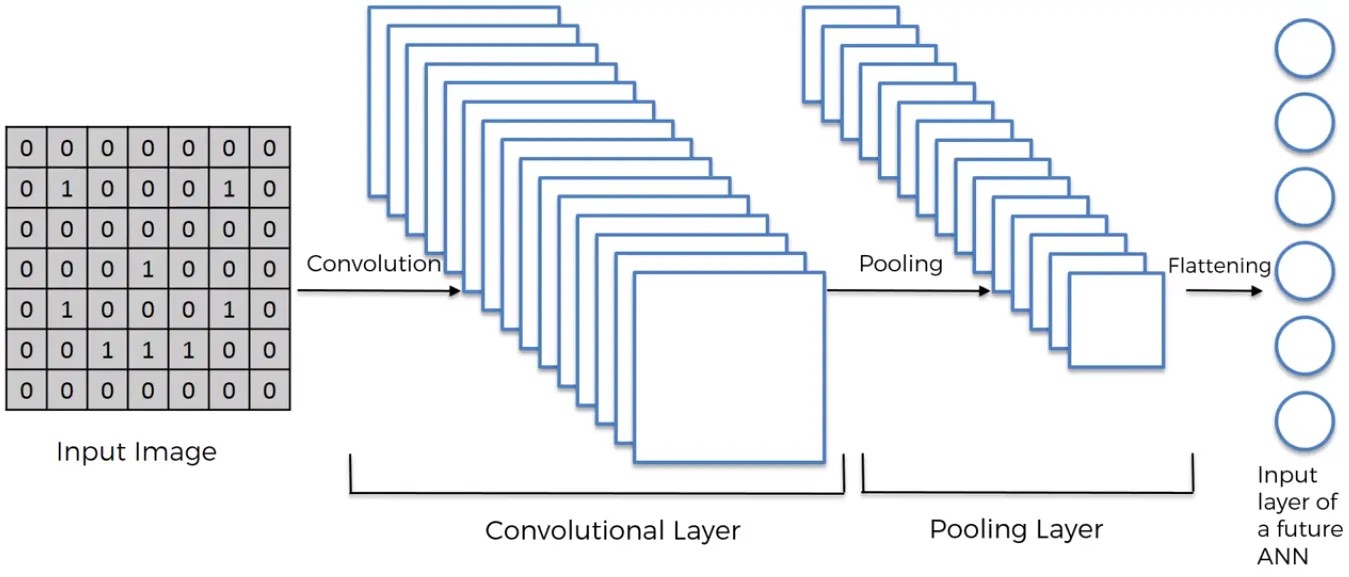
• Components

  

  • 합성곱 레이어(Convolution Layer)
  • 합동 레이어(Pooling Layer)
  • 평탄화 레이어(Flatten Layer)
  • 완전 연결 계층(Fully-Connected Layer)

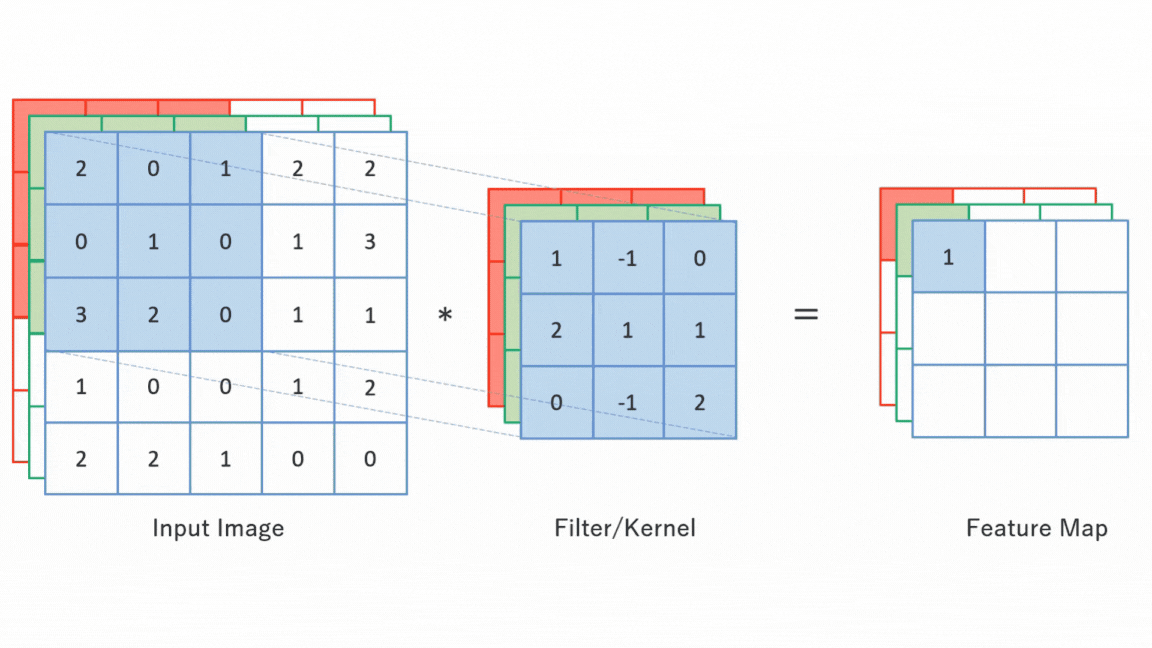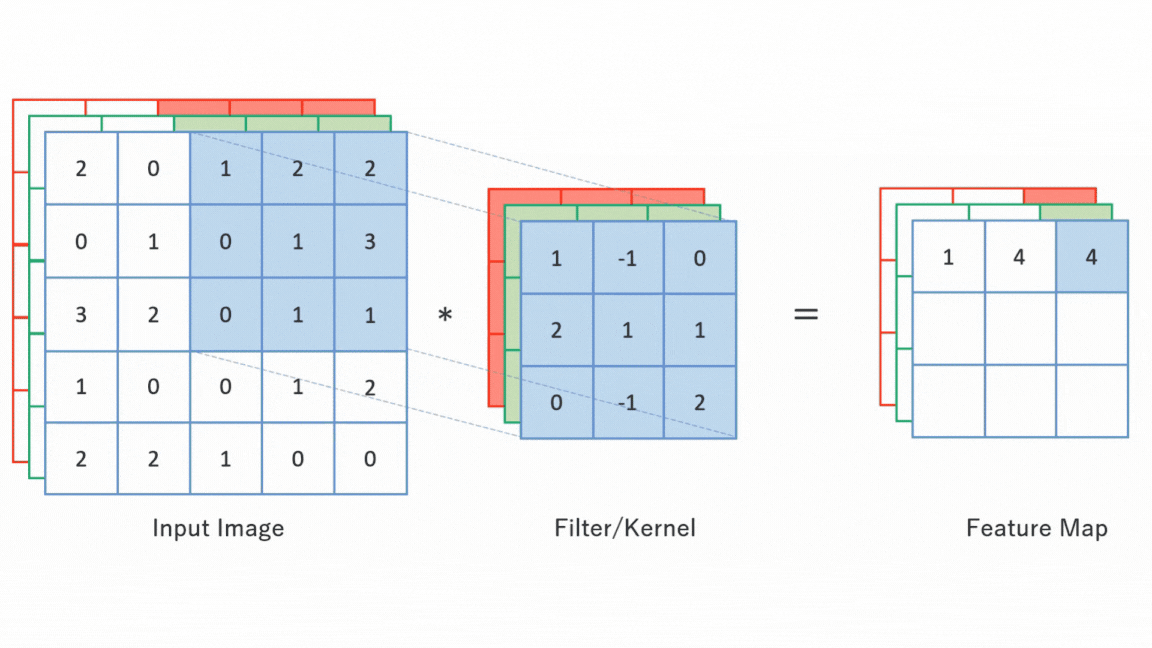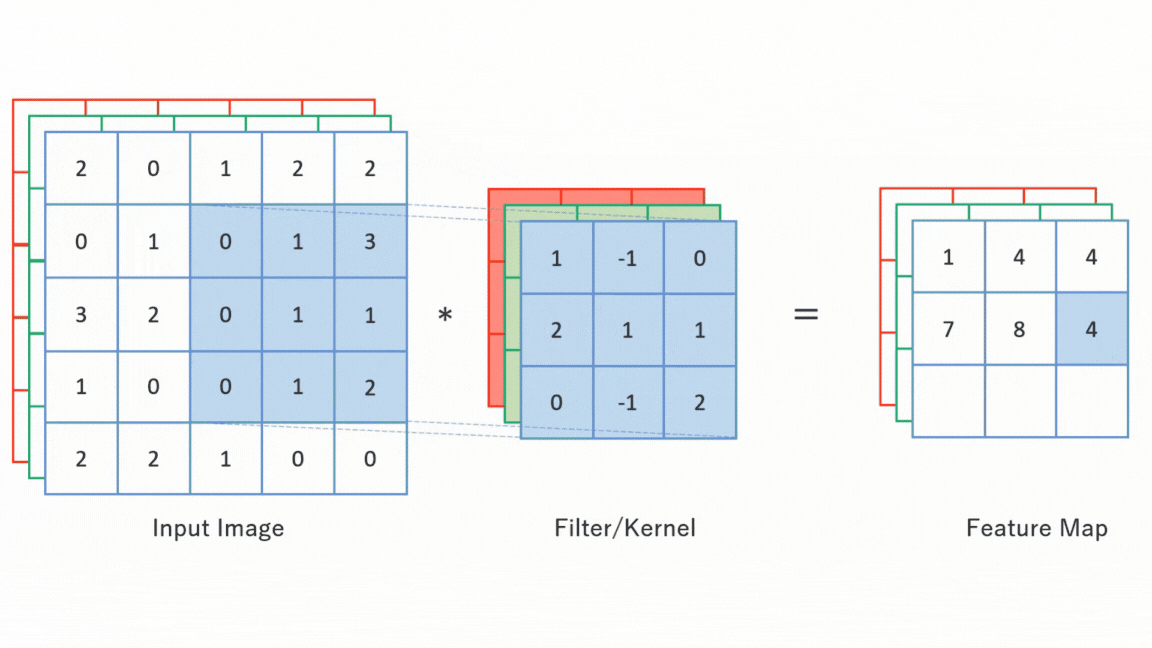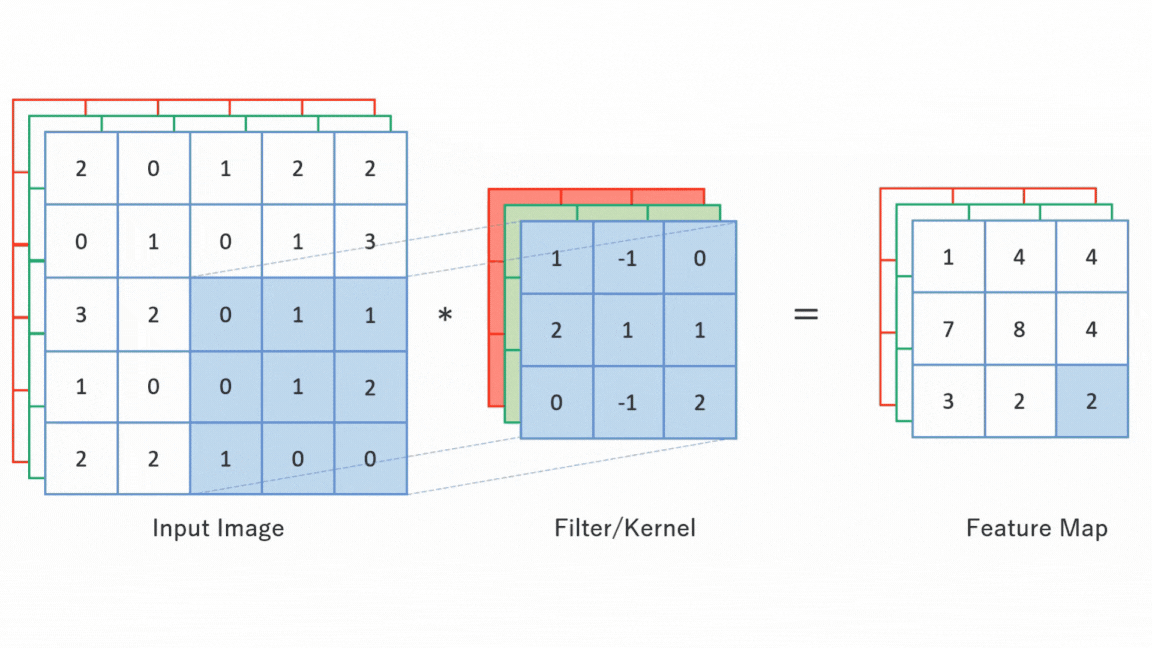
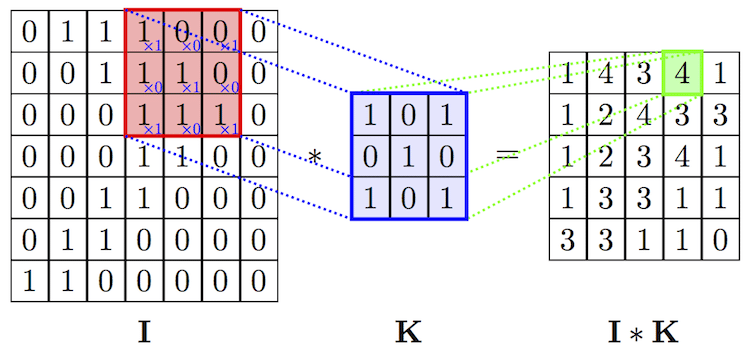
• 합성곱 연산(Convolution Operation): 입력값의 부분 공간을 커널(Kernel)과 요소별 곱셈(Element-wise Product) 및 그 결과를 합산하여 피처 맵(Feature Map)을 추출하는 연산

  

• 커널(Kernel): 입력값의 부분 공간과 요소별 곱셈(Element-wise Product)하는 여과기(Filter)

  

• 피처 맵(Feature Map) : 합성곱 연산 결과 입력값 형상의 특징으로서 반환된 새로운 배열로서 원소값은 부분 공간이 커널과 매칭되는 정도를 나타냄

  

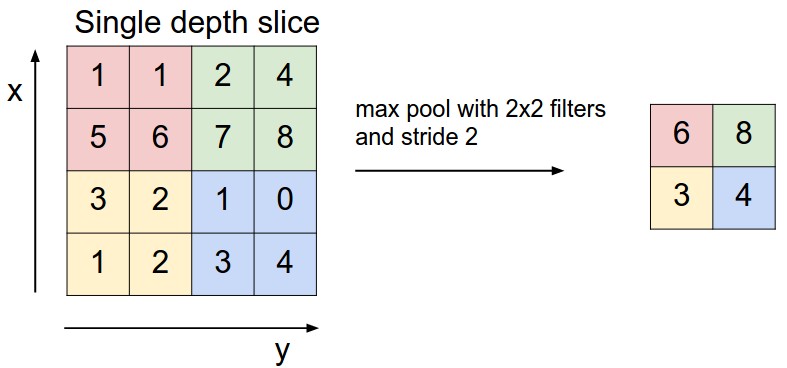
• 합동 연산(Pooling Operation): 피처 맵(Featur Map)에 대하여 그 부분 공간마다 대표값을 추출하여 요약된 행렬을 구성하는 연산

  

---

Sourse

• https://medium.com/@PK_KwanG/cnn-step-2-flattening-50ee0af42e3e
• https://medium.com/@alejandro.itoaramendia/convolutional-neural-networks-cnns-a-complete-guide-a803534a1930