Chi-Squared and Extension

Chi-Squared

---

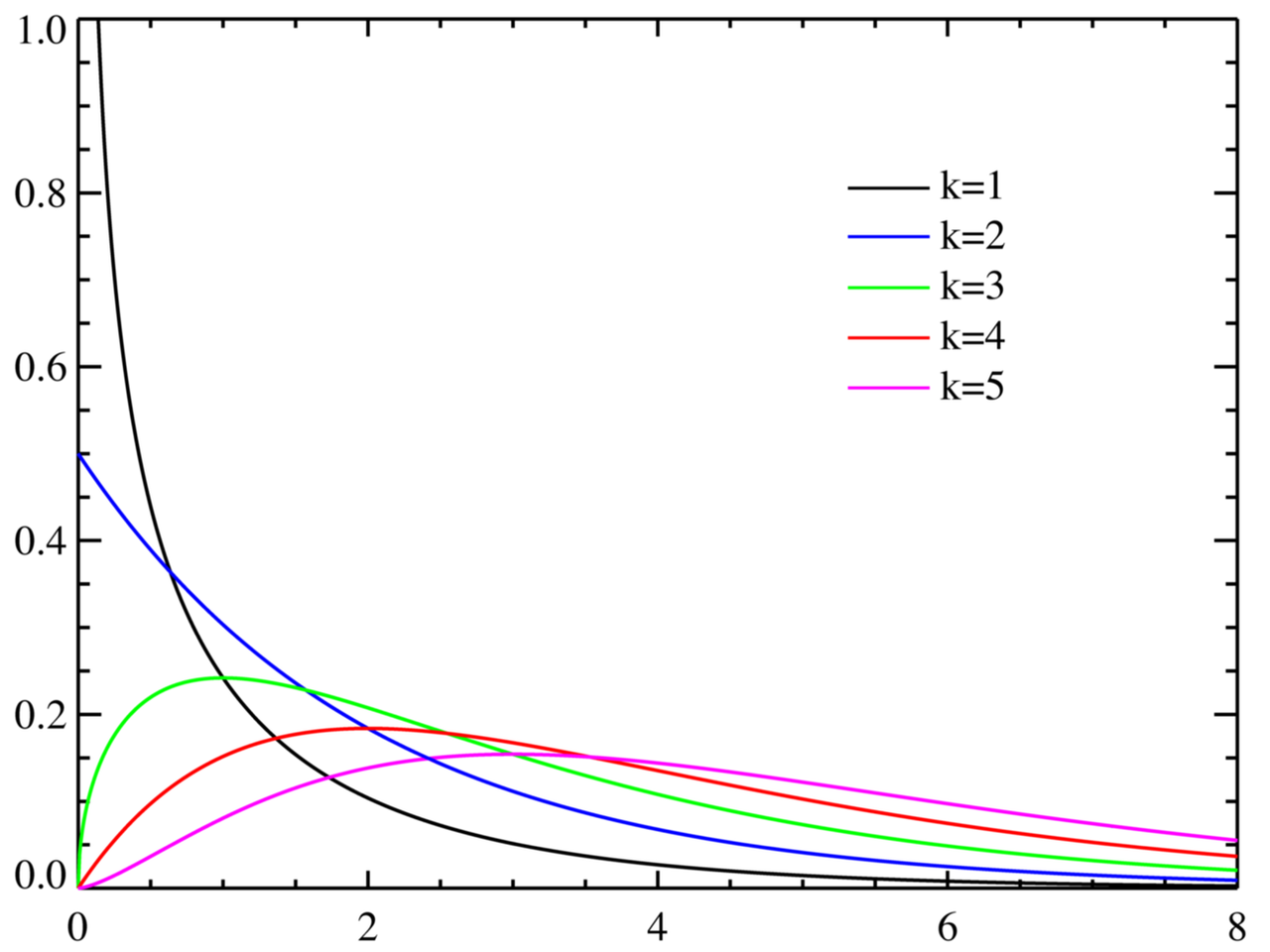
• 카이제곱 분포(chi-squared distribution): 가우시안 확률변수 자승의 누적량에 대한 분포

  \[\begin{aligned} X:=\sum_{i=1}^{k}{Z_{i}^{2}}\sim\chi^{2}(k)\quad\mathrm{for}\quad \forall Z\overset{\text{i.i.d}}{\sim}\mathcal{N}(0,1) \end{aligned}\]

• The chi-square distribution can be viewed as a special form of the gamma distribution in that it deals with the cumulative amount of positive physical quantities:

  \[\begin{aligned} \mathrm{Gamma}\left(\alpha=\frac{k}{2},\beta=\frac{1}{2}\right) &=\frac{(1/2)^{k/2}}{\Gamma(k/2)}x^{k/2-1}\exp{\left[-\frac{1}{2}x\right]}\\ &=\frac{1}{2^{k/2}\Gamma(k/2)}x^{k/2-1}\exp{\left[-\frac{1}{2}x\right]}\\ &=\chi^{2}(k) \end{aligned}\]

• probability density function:

  \[\begin{aligned} p(x) =\frac{1}{2^{k/2}\Gamma(k/2)}x^{k/2-1}\exp{\left[-\frac{1}{2}x\right]} \end{aligned}\]

• moment generating function:

  \[\begin{aligned} M_{X}(t) &=\mathbb{E}_{p(x)}\left[\exp{tX}\right]\\ &=\int_{0}^{\infty}{\exp{tx}\frac{1}{2^{k/2}\Gamma(k/2)}x^{k/2-1}\exp{\left[-\frac{1}{2}x\right]}\mathrm{d}x}\\ &=\frac{1}{2^{k/2}\Gamma(k/2)}\int_{0}^{\infty}{x^{k/2-1}\exp{\left[-\left(\frac{1}{2}-t\right)x\right]}\mathrm{d}x}\\ \\ \frac{1}{\beta^{\alpha}}\Gamma(\alpha) &:=\int_{0}^{\infty}{x^{\alpha-1}\exp{-\beta x}\mathrm{d}x},\quad\alpha,\beta>0\\ \\ \therefore M_{X}(t) &=\frac{1}{2^{k/2}\Gamma(k/2)}\cdot\frac{\Gamma(k/2)}{(1/2-t)^{k/2}}\\ &=\left(\frac{1}{1-2t}\right)^{k/2} \end{aligned}\]
  • $\mathbb{E}\left[X\right]=(\mathrm{d}/\mathrm{d}t)M_{X}(t)\vert_{t=0}=k$
  • $\mathbb{E}\left[X^{2}\right]=(\mathrm{d}^{2}/\mathrm{d}t^{2})M_{X}(t)\vert_{t=0}=k(k+2)$
  • $\mathrm{Var}\left[X\right]=\mathbb{E}\left[X^{2}\right]-\mathbb{E}\left[X\right]^{2}=2k$

• canonical form:

  \[\begin{aligned} p(x) &=\frac{1}{2^{k/2}\Gamma(k/2)}x^{k/2-1}\exp{\left[-\frac{1}{2}x\right]}\\ &=\exp{\left[-\frac{k}{2}\log{2}-\log{\Gamma\left(\frac{k}{2}\right)}\right]}\cdot\exp{\left[\left(\frac{k}{2}-1\right)\log{x}\right]}\cdot\exp{\left[-\frac{1}{2}x\right]}\\ &=1\cdot\exp{\left[\begin{pmatrix}k/2-1\\-1/2\end{pmatrix}^{T}\begin{pmatrix}\log{x}\\x\end{pmatrix}-\left\{\frac{k}{2}\log{2}+\log{\Gamma\left(\frac{k}{2}\right)}\right\}\right]} \end{aligned}\]
  • $T(x)=\log{x},x$
  • $\eta(\theta)=k/2-1,-1/2$
  • $A(\eta)=(k/2)\log{2}+\log{\Gamma(k/2)}$
  • $h(x)=1$

Wishart

---

• 위샤트 분포(Wishart Distribution): 카이제곱 분포의 다변량 분포로서, 다변량 가우시안 확률변수에 대하여, 그 독립 표본들의 외적의 누적량을 나타내는 분포

  \[S:=\sum_{i=1}^{\nu}{\mathbf{x}_{i}\mathbf{x}_{i}^{T}}\sim\mathcal{W}_{P}(\nu,\Sigma)\quad\mathrm{for}\quad\mathbf{x}_{i}\overset{\mathrm{i.i.d}}{\sim}\mathcal{N}_{P}(0,\Sigma)\]
  • $S\in\mathbb{R}^{P\times P}$: 독립 표본들의 산점도 행렬로서 양정치 행렬
  • $\nu$: 자유도로서 형상 파라미터
  • $\Sigma\in\mathbb{R}^{P\times P}$: 독립 표본들의 공분산 행렬로서 스케일 파라미터

• probability density function:

  \[p(S\mid\Sigma) =\frac{1}{2^{np/2}\mathrm{det}(\Sigma)^{n/2}\Gamma_{P}(n/2)}\mathrm{det}(S)^{(n-p-1)/2}\exp{\left[-\frac{1}{2}\mathrm{tr}\left(\Sigma^{-1}S\right)\right]}\]

• moment generating function:

  \[\begin{aligned} M_{S}(T) &=\mathbb{E}_{p(S)}\left[\exp{\mathrm{tr}\left(TS\right)}\right]\\ &=\int_{S>0}{\exp{\mathrm{tr}\left(TS\right)\cdot\frac{1}{2^{np/2}\mathrm{det}(\Sigma)^{n/2}\Gamma_{P}(n/2)}\mathrm{det}(S)^{(n-p-1)/2}\exp{\left[-\frac{1}{2}\mathrm{tr}\left(\Sigma^{-1}S\right)\right]}}\mathrm{d}S}\\ &=\frac{1}{2^{np/2}\mathrm{det}(\Sigma)^{n/2}\Gamma_{P}(n/2)}\int_{S>0}{\mathrm{det}(S)^{(n-p-1)/2}\exp{\left[\mathrm{tr}\left(TS\right)-\frac{1}{2}\mathrm{tr}\left(\Sigma^{-1}S\right)\right]}\mathrm{d}S}\\ \\ \mathrm{tr}\left(TS\right)-\frac{1}{2}\mathrm{tr}\left(\Sigma^{-1}S\right) &=\mathrm{tr}\left(TS\right)+\mathrm{tr}\left(-\frac{1}{2}\Sigma^{-1}S\right)\\ &=\mathrm{tr}\left(TS-\frac{1}{2}\Sigma^{-1}S\right)\\ &=-\frac{1}{2}\mathrm{tr}\left(\left[\Sigma^{-1}-2T\right]S\right)\\ \\ \because\int_{S>0}{p(S)\mathrm{d}S} &=1\\ \int_{S>0}{\mathrm{det}(S)^{(n-p-1)/2}\exp{\left[-\frac{1}{2}\mathrm{tr}\left(\Sigma^{-1}S\right)\right]}\mathrm{d}S} &=2^{np/2}\mathrm{det}(\Sigma)^{n/2}\Gamma_{P}(n/2)\\ \int_{S>0}{\mathrm{det}(S)^{(n-p-1)/2}\exp{\left[-\frac{1}{2}\mathrm{tr}\left(\left[\Sigma^{-1}-2T\right]S\right)\right]}\mathrm{d}S} &=2^{np/2}\mathrm{det}(\Sigma^{-1}-2T)^{-n/2}\Gamma_{P}(n/2)\\ \\ \therefore M_{S}(T) &=\frac{1}{2^{np/2}\mathrm{det}(\Sigma)^{n/2}\Gamma_{P}(n/2)}\cdot 2^{np/2}\mathrm{det}(\Sigma^{-1}-2T)^{-n/2}\Gamma_{P}(n/2)\\ &=\mathrm{det}(\Sigma)^{-n/2}\mathrm{det}(\Sigma^{-1}-2T)^{-n/2}\\ &=\mathrm{det}(\Sigma)^{-n/2}\cdot\mathrm{det}(\Sigma)^{n/2}\mathrm{det}(I-2\Sigma T)^{-n/2}\\ &=\mathrm{det}(I-2\Sigma T)^{-n/2} \end{aligned}\]
  • $\mathbb{E}\left[S_{i,j}\right]=\nabla_{T}M_{S}(T)\vert_{T=0}=n\cdot\Sigma_{i,j}$
  • $\mathbb{E}\left[S_{i,j}S_{k,l}\right]=\nabla_{T}^{2}M_{S}(T)\vert_{T=0}=n(\Sigma_{i,k}\Sigma_{j,l}+\Sigma_{i,l}\Sigma_{j,k})+n^{2}\Sigma_{i,j}\Sigma_{k,l}$
  • $\mathrm{Cov}\left[S_{i,j},S_{k,l}\right]=\mathbb{E}\left[S_{i,j}S_{k,l}\right]-\mathbb{E}\left[S_{i,j}\right]\mathbb{E}\left[S_{k,l}\right]=n(\Sigma_{i,k}\Sigma_{j,l}+\Sigma_{i,l}\Sigma_{j,k})$

• canonical form:

  \[\begin{aligned} p(S) &=\frac{1}{2^{\nu p/2}\mathrm{det}(\Sigma)^{\nu/2}\Gamma_{P}(\nu/2)}\mathrm{det}(S)^{(\nu-p-1)/2}\exp{\left[-\frac{1}{2}\mathrm{tr}\left(\Sigma^{-1}S\right)\right]}\\ &=\exp{\left[-\frac{\nu p}{2}\log{2}-\frac{\nu}{2}\log{\mathrm{det}(\Sigma)}-\log{\Gamma_{P}\left(\frac{\nu}{2}\right)}\right]}\exp{\left[\frac{\nu-p-1}{2}\log{\mathrm{det}(S)}\right]}\exp{\left[-\frac{1}{2}\mathrm{tr}\left(\Sigma^{-1}S\right)\right]}\\ &=1\cdot\exp{\left[\begin{pmatrix}\frac{\nu-p-1}{2}\\-\frac{1}{2}\Sigma^{-1}\end{pmatrix}^{T}\begin{pmatrix}\log{\mathrm{det}(S)}\\S\end{pmatrix}-\left(\frac{\nu}{2}\log{\mathrm{det}(\Sigma)}+\log{\Gamma_{P}\left(\frac{\nu}{2}\right)}+\frac{\nu p}{2}\log{2}\right)\right]} \end{aligned}\]
  • $T(S)=\log{\mathrm{det}(S)},S$
  • $\eta(\theta)=(\nu-p-1)/2,-(1/2)\Sigma^{-1}$
  • $A(\eta)=(\nu/2)\log{\mathrm{det}(\Sigma)}+\log{\Gamma_{P}(\nu/2)}+(\nu p/2)\log{2}$
  • $h(S)=1$