Clustering
Based on the lecture “Intro. to Machine Learning (2023-2)” by Prof. Je Hyuk Lee, Dept. of Data Science, The Grad. School, Kookmin Univ.
Cluster Analysis
-
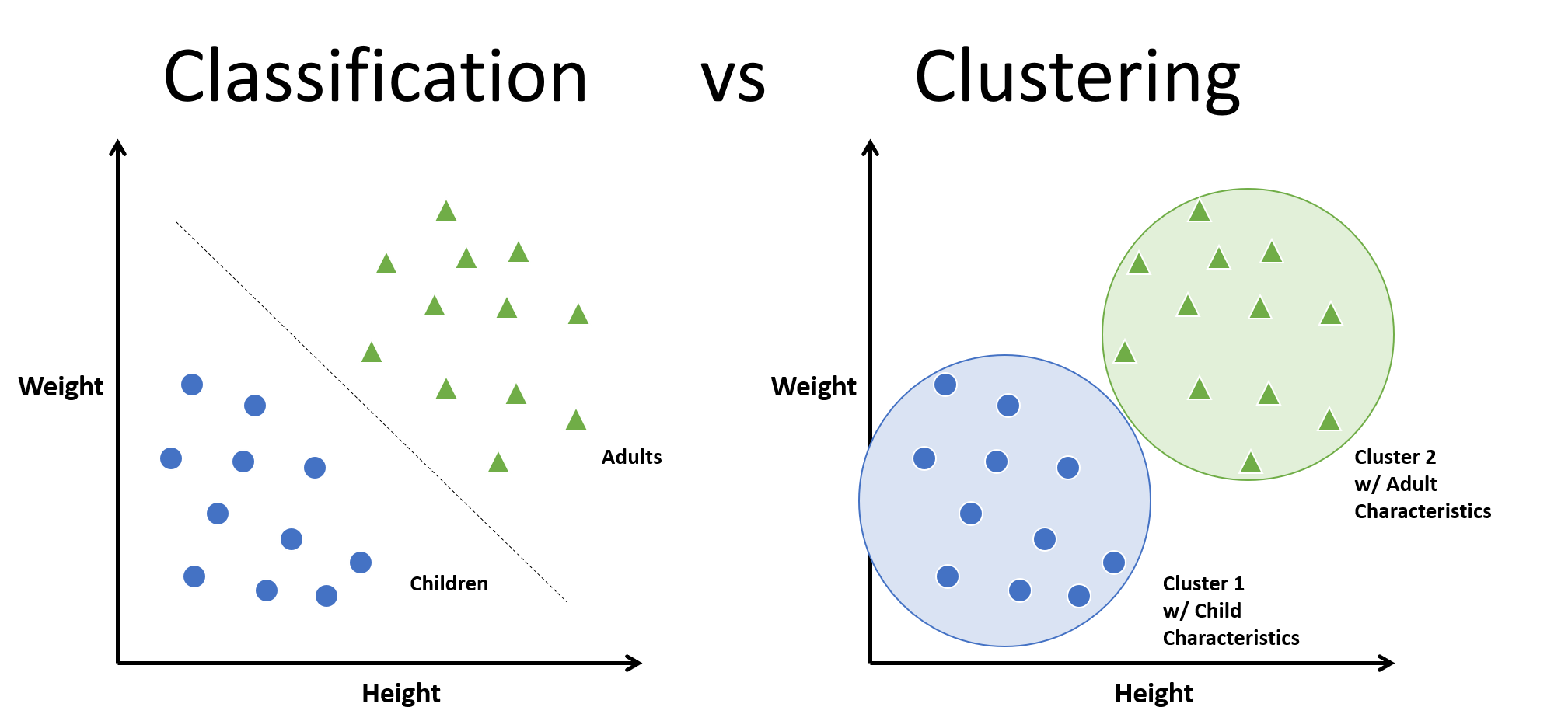
군집 분석(Cluster Analysis): 표본을 관측치 간 유사성과 상이성을 계산하여 군집 내 응집도를 최대화하는 동시에 군집 간 분리도를 최대화하는 $k$ 개의 군집으로 분할하는 작업
Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group are more similar to each other than to those in other groups. (by.Wikipedia)
-
구분
- Hard(or Crisp) Clustering
- Soft(or Fuzzy) Clustering
- Partitional Clustering
- Hierarchical Clustering
Metrics
- External : 정답 정보와의 비교
- Rand Statistic
- Jaccard Coefficient
- Folks and Mallows Index
- Hurbert $\Gamma$ Statistic
- V-Measure
- Internal : 군집 내 응집도
- Cophenetic Correlation Coefficient
- Sum of Squared Error(SSE)
- Cohesion and Separation
- Relative : 군집 간 분리도
- Dunn Family of Indices
- Davies-Bouldin Index
- Semi-partial R-squared
- SD Validity Index
- Silhouette
External Metrics
-
V-Measure : 정확성과 완전성의 조화평균
\[\begin{aligned} \text{V} &= 2\times\frac{H(C \mid K) \cdot C(K \mid C)}{H(C \mid K) + C(K \mid C)} \end{aligned}\]- $H(C \mid K)$ : 정확성(Homogeneity)
- $C(K \mid C)$ : 완전성(Completeness)
-
정확성(Homogeneity) : 각 군집의 클래스에 대한 엔트로피 합계
\[\begin{aligned} H(C \mid K) &= -\sum_{k=1}^{K}{\sum_{c=1}^{C}{P(c \mid k) \cdot \log{P(c \mid k)}}} \end{aligned}\]- $k$ : 군집 번호
- $c$ : 클래스 번호
- $P(c \mid k)$ : 군집 $K=k$ 가 주어졌을 때, 클래스 $C=c$ 가 발생할 가능성
-
완전성(Completeness) : 각 클래스의 군집에 대한 엔트로피 합계
\[\begin{aligned} C(K \mid C) &= -\sum_{c=1}^{C}{\sum_{k=1}^{K}{P(k \mid c) \cdot \log{P(k \mid c)}}} \end{aligned}\]- $P(k \mid c)$ : 클래스 $C=c$ 가 주어졌을 때, 군집 $K=k$ 가 발생할 가능성
Internal Metrics
-
Sum of Squared Error(SSE) : 각 군집의 중심점 벡터와 해당 군집 내 관측치 벡터 간 거리 자승으로 측정한 군집 응집도
\[\begin{aligned} \text{SSE} &= \sum_{k=1}^{K}{\sum_{\mathbf{x}_{i} \in C_{k}}{\Vert \mathbf{x}_{i}-\mu_{k} \Vert^2}} \end{aligned}\]- $k$ : 군집 번호
- $C_{k}$ : $k$ 번째 군집
- \(\mathbf{x}_{i} \in C_{k}\) : 군집 \(C_{k}\) 의 $i$ 번째 관측치 벡터
- \(\mu_{k} \in C_{k}\) : 군집 \(C_{k}\) 의 중심 벡터
Relative Metrics
-
Dunn Index : 군집 내 응집도(Cohesion) 최대값 대비 군집 간 분리도(Separation) 최소값 비율
\[\begin{aligned} \text{DI} &= \frac{\min_{1 \le i \ne j \le K}{d_{C}(C_{i},C_{j})}}{\max_{1 \le k \le K}{\Delta(C_{k})}} \end{aligned}\]- $\min_{1 \le i \ne j \le K}{d_{C}(C_{i},C_{j})}$ : 군집 간 분리도 최소값으로서 분리도에 대한 최악의 경우
- $\max_{1 \le k \le K}{\Delta(C_{k})}$ : 군집 내 응집도 최대값으로서 응집도에 대한 최악의 경우
-
실루엣 계수(Silhouette) : 군집 내 응집성(cohesion)과 군집 간 분리도(separation)를 종합적으로 고려하여 측정한 개별 관측치 벡터에 대한 군집화 적합성의 평균값
\[\begin{aligned} \text{S} &= \frac{1}{n}\sum_{i=1}^{n}{\frac{b(\mathbf{x}_{i})-a(\mathbf{x}_{i})}{\max{[a(\mathbf{x}_{i}),b(\mathbf{x}_{i})]}}} \end{aligned}\]- \(a(\mathbf{x}_{i})\) : 관측치 벡터 \(\mathbf{x}_{i}\) 기준 군집 내 응집도로서, 해당 관측치와 같은 군집에 속한 관측치와의 평균 거리
- \(b(\mathbf{x}_{i})\) : 관측치 벡터 \(\mathbf{x}_{i}\) 기준 군집 간 분리도로서, 해당 관측치와 다른 군집에 속한 관측치와의 평균 거리 중 최소값
Sourse
- https://www.scaler.com/topics/supervised-and-unsupervised-learning/
- https://towardsdatascience.com/a-brief-introduction-to-unsupervised-learning-20db46445283
- https://tyami.github.io/machine%20learning/clustering/