DBSCAN

DBSCAN

---

• DBSCAN(Density-Based Spatial Clustering of Applications with Noise) : 밀도 기반 배타적 분리형 군집화 알고리즘

  

• 군집 : 사전에 주어진 $\varepsilon, \text{MinPts}$ 에 기초했을 때 Maximality, Connectivity 조건을 만족하는 Non-Empty Subset

  

  • Maximality

    표본 $D$ 에 속하는 관측치 벡터 $\mathbf{p}, \mathbf{q}$ 에 대하여, $\mathbf{p} \in C \subseteq D$ 이고, $\mathbf{q}$ 가 $\mathbf{p}$ 로부터 밀도 기준 도달 가능한(Directly Density-Reachable) 벡터이면, $\mathbf{q} \in C$ 임

  • Connectivity

    군집 $C$ 에 속하는 관측치 벡터 $\mathbf{p}, \mathbf{q}$ 간에는 밀도 기준 연결되어 있음(Density-Connected)

Concept

---

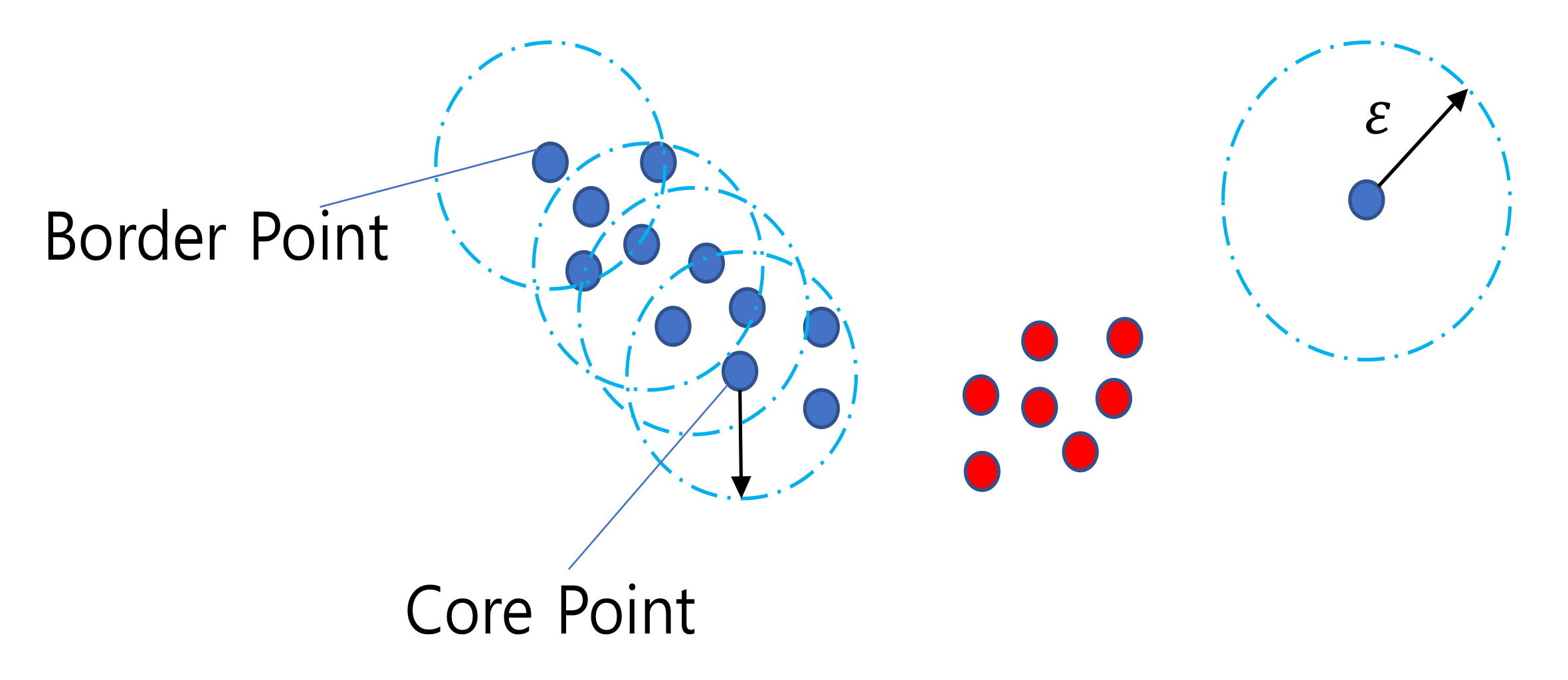
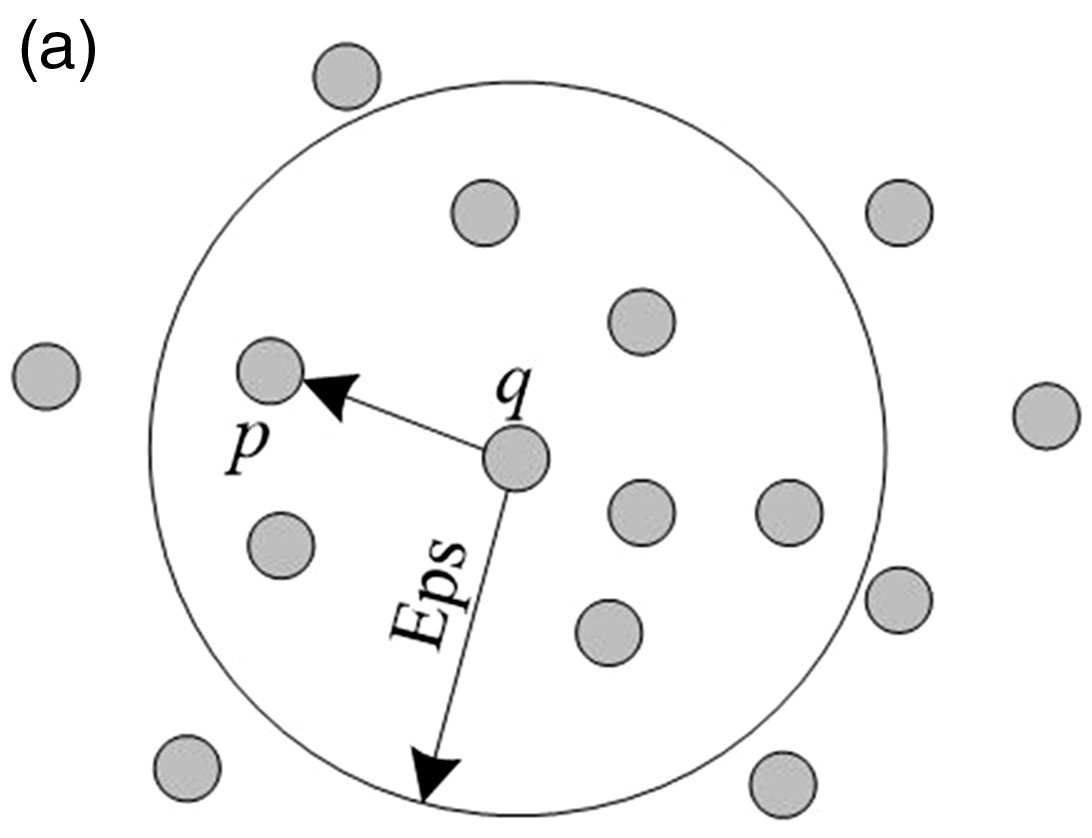
$\varepsilon$-neighborhood of a point

표본 $D$ 에 속하는 관측치 벡터 $\mathbf{p}$ 에 대하여, $\mathbf{p}$ 의 이웃 집합 $N_{\varepsilon}(\mathbf{p})$ 은 $\mathbf{p}$ 와의 거리가 $\varepsilon$ 이하인 관측치 벡터 $\mathbf{q}$ 의 집합임

\[N_{\varepsilon}(\mathbf{p}) =\{\mathbf{q} \in D \mid d(\mathbf{p},\mathbf{q}) \le \varepsilon\}\]

Directly Density-Reachable

Core Point Condition 을 만족하는 관측치 벡터 $\mathbf{p} \in D$ 에 대하여, 그 이웃 관측치 벡터($\varepsilon$-neighborhood of a point) $\mathbf{q}$ 는 $\mathbf{p}$ 로부터 밀도 기준 직접 도달 가능한(Directly Density-Reachable) 관측치 벡터임

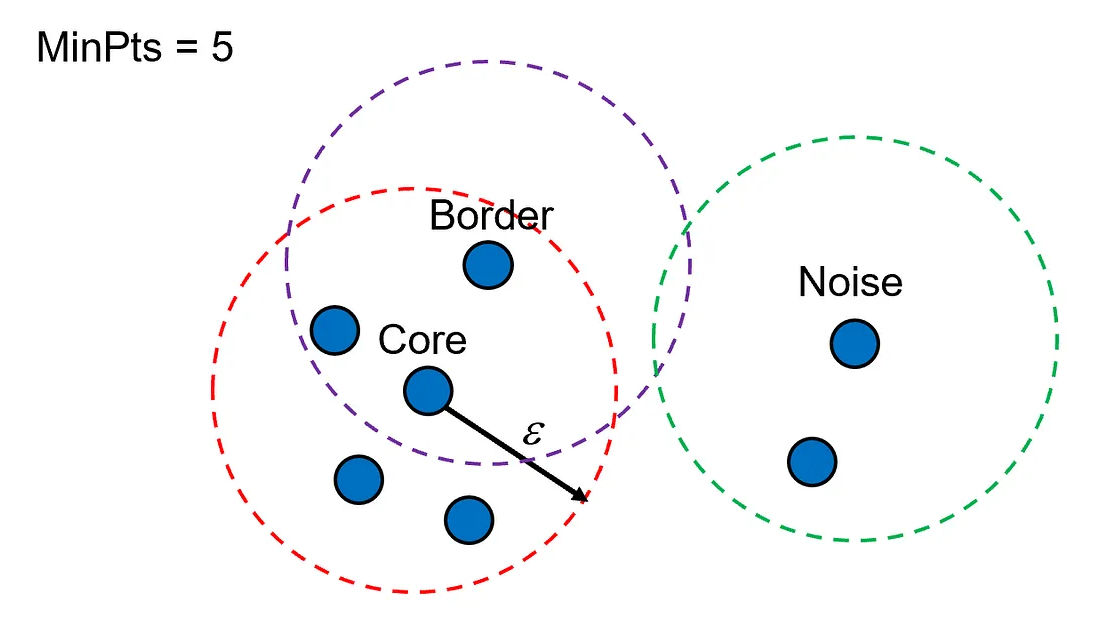
• Core Point Condition

  \[\vert N_{\varepsilon}(\mathbf{p}) \vert \ge \text{MinPts}\]

• Reachability

  \[\mathbf{q} \in N_{\varepsilon}(\mathbf{p})\]

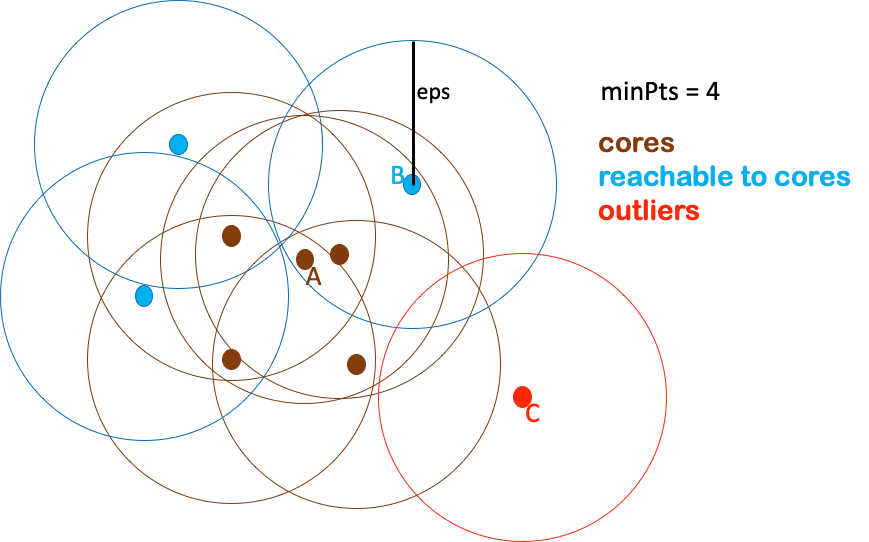
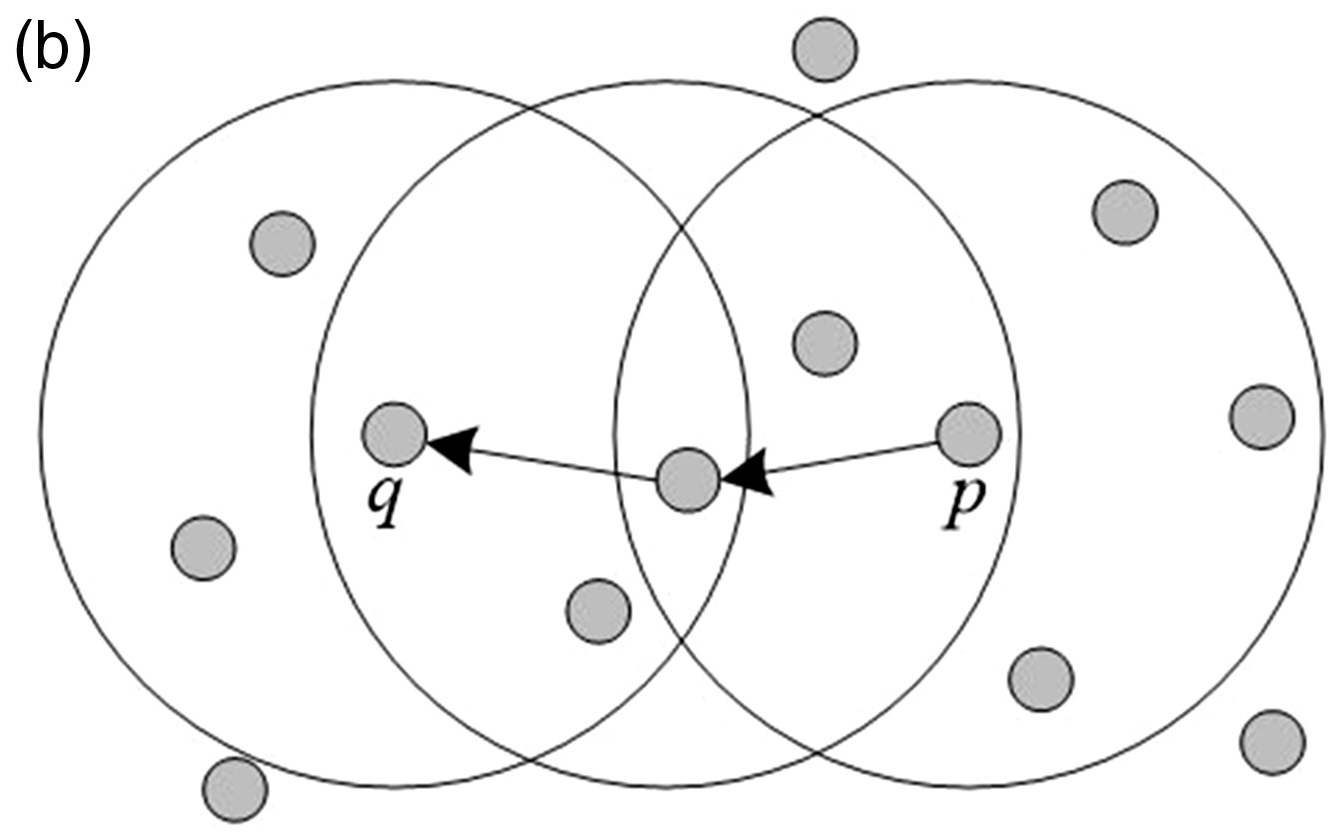
Density-Reachable

Core Point Condition 을 만족하는 관측치 벡터 \(\mathbf{p} \in D\) 에 대하여, \(\mathbf{p}\) 와 \(\mathbf{q}\) 사이에 \(\mathbf{p}\) 로부터 밀도 기준 직접 도달 가능한 관측치 벡터 \(\mathbf{x}_{1},\mathbf{x}_{2},\cdots,\mathbf{x}_{n}\) 이 연쇄적으로 존재한다면, \(\mathbf{q}\) 는 \(\mathbf{p}\) 로부터 밀도 기준 도달 가능한(Density-Reachable) 관측치 벡터임

• \(\vert N_{\varepsilon}(\mathbf{p})\vert \ge \text{MinPts}\) : Core Point Condition
• \(\mathbf{x}_{1} \in N_{\varepsilon}(\mathbf{p})\) : Reachability
• \(\vert N_{\varepsilon}(\mathbf{x}_{\forall})\vert \ge \text{MinPts}\) : \(\mathbf{x}_{\forall}\) 의 이웃 벡터 갯수가 하한선 $\text{MinPts}$ 이상임
• \(\mathbf{x}_{i+1} \in N_{\varepsilon}(\mathbf{x}_{i})\) : \(\mathbf{x}_{i+1}\) 는 \(\mathbf{x}_{i}\) 의 이웃 벡터임
• \(\mathbf{q} \in N_{\varepsilon}(\mathbf{x}_{n})\) : \(\mathbf{q}\) 는 \(\mathbf{x}_{n}\) 의 이웃 벡터임

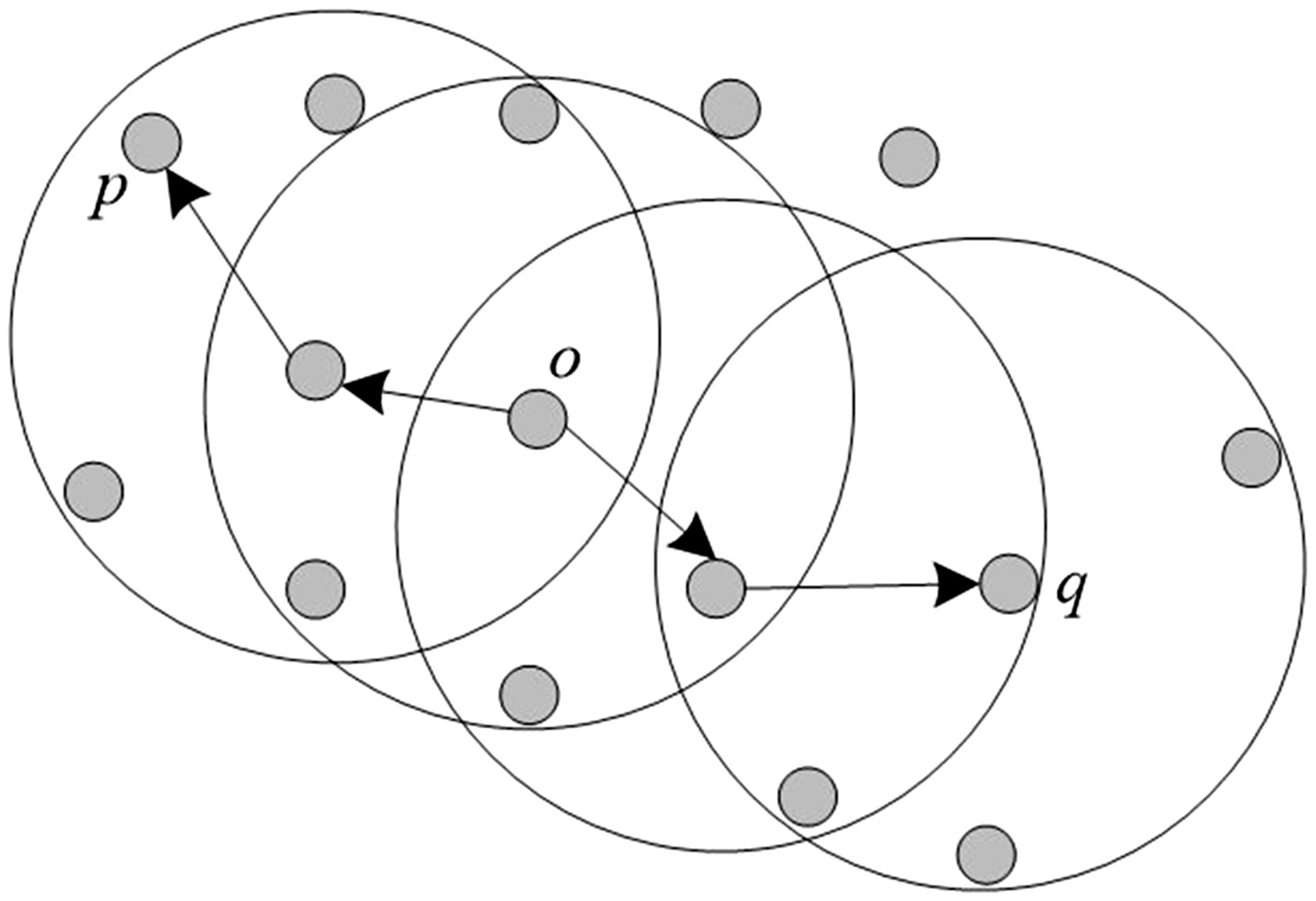
Density-Connected

Core Point Condition 을 만족하는 관측치 벡터 \(\mathbf{p},\mathbf{q} \in D\) 에 대하여, \(\mathbf{p}\) 로부터 밀도 기준 도달 가능한(Density-Connected) 동시에 \(\mathbf{q}\) 로부터 밀도 기준 도달 가능한(Density-Connected) 관측치 벡터 \(\mathbf{x} \in D\) 가 적어도 하나 존재한다면, \(\mathbf{p},\mathbf{q}\) 는 밀도 기준 연결되어 있음(Density-Connected)

• $\vert N_{\varepsilon}(\mathbf{p})\vert \ge \text{MinPts}$
• $\mathbf{x} \in N_{\varepsilon}(\mathbf{p})$
• $\vert N_{\varepsilon}(\mathbf{q})\vert \ge \text{MinPts}$
• $\mathbf{x} \in N_{\varepsilon}(\mathbf{q})$

---

Sourse

• https://ai.plainenglish.io/dbscan-density-based-clustering-aaebd76e2c8c
• https://journals.sagepub.com/doi/10.1177/1748301817735665