Distance Embedding based Latent Factor Model

Learning Objectives

---

• 표현 학습(Representation Learning)
  • 사용자와 아이템을 공동의 잠재요인 공간에 표현하는 방법
  • 매칭 강도 추정 시 내적(Inner Product) 등 선형 유사도 함수를 적용함
  • 저차원(Low-rank) 유사도 구조를 효율적으로 포착할 수 있음
• 매칭 함수 학습(Matching Function Learning)
  • 사용자-아이템 쌍을 입력으로 하여 매칭 함수를 직접 학습하는 방법
  • 복잡하고 비선형적인 매칭 함수를 근사할 수 있음

DDFL

---

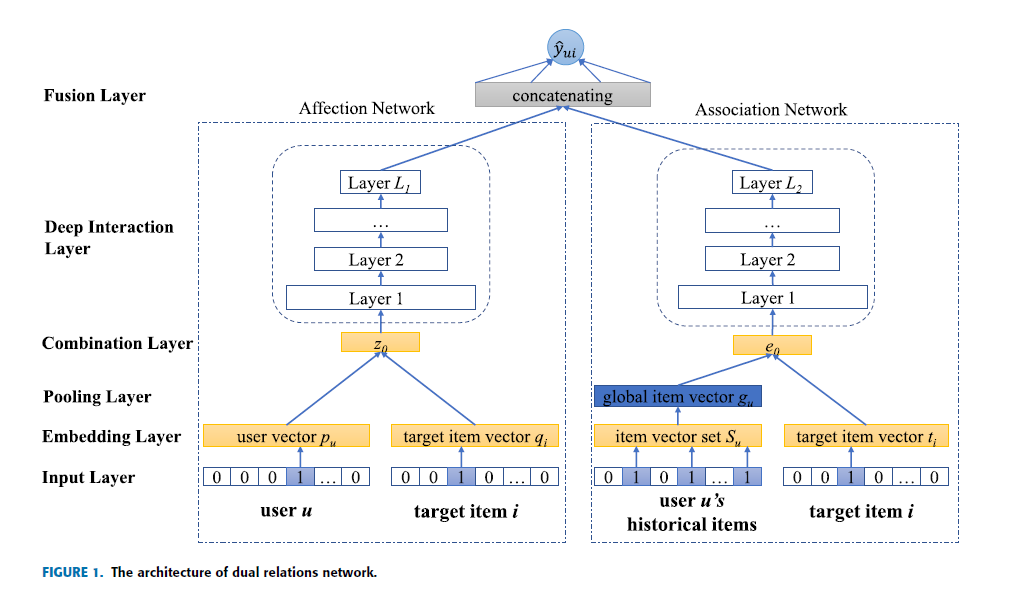
• 문제 의식: 내적(Dot Product) 혹은 코사인 유사도(Cosine Similarity)를 매칭 함수로 사용하여 학습된 사용자, 아이템 표현은 삼각 부등식(Triangular Inequality)을 만족하기 어려움

• 삼각 부등식(Triangular Inequality)

  • 세 점 사이의 거리에 대한 제한 조건으로서, $A$ 와 $C$ 사이 거리는 $A$ 에서 $B$, 그리고 $B$ 에서 $C$ 로 우회하는 거리보다 크거나 같아야 함

    \[\begin{aligned} \text{d}\left[A,C\right] \le \text{d}\left[A,B\right] + \text{d}\left[B,C\right] \end{aligned}\]

  • 사용자 $u$ 가 아이템 $i$ 를 직접적으로 선호하는 정도는, 사용자 $u$ 가 아이템 $j$ 를 선호하는 정도 및 아이템 $i$ 와 $j$ 간 유사한 정도의 합보다 작거나 같아야 함

    \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u} \cdot \overrightarrow{\mathbf{q}}_{i} \le \overrightarrow{\mathbf{p}}_{u} \cdot \overrightarrow{\mathbf{q}}_{j} + \overrightarrow{\mathbf{q}}_{i} \cdot \overrightarrow{\mathbf{q}}_{j} \end{aligned}\]
• DDFL(Deep Dual Function Learning-based Model) : 거리 함수 학습 모듈과 매칭 함수 학습 모듈을 병렬 학습하는 앙상블 모형
  • Shah, S. T. U., Li, J., Guo, Z., Li, G., & Zhou, Q.
    (2020, September).
    DDFL: a deep dual function learning-based model for recommender systems.
    In International Conference on Database Systems for Advanced Applications (pp. 590-606).
    Cham: Springer International Publishing.
• Components
  • MeFL: Metric Function Learning
  • MaFL: Matching Function Learning
  • DDFL: MeFL & MaFL Ensemble

Notation

---

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\mathbf{Y} \in \mathbb{R}^{M \times N}$: user-item interaction matrix
• $\overrightarrow{\mathbf{p}}_{u} \in \mathbb{R}^{K}$: user latent factor vector @ MeFL
• $\overrightarrow{\mathbf{q}}_{i} \in \mathbb{R}^{K}$: item latent factor vector @ MeFL
• $\overrightarrow{\mathbf{u}}_{u} \in \mathbb{R}^{K}$: user latent factor vector @ MaFL
• $\overrightarrow{\mathbf{v}}_{i} \in \mathbb{R}^{K}$: item latent factor vector @ MaFL
• $\overrightarrow{\mathbf{z}}_{u,i}$: predictive vector of user $u$ and item $i$
• $\hat{y}_{u,i}$: interaction probability of user $u$ and item $i$

How to Modeling

---

• DDFL is MeFL & MaFL Ensemble:

  • predictive vector of user $u$ and item $i$:

    \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{z}}_{u,i}^{\text{(MeFL)}} \oplus \overrightarrow{\mathbf{z}}_{u,i}^{\text{(MaFL)}}) \end{aligned}\]

  • final matching score of user $u$ and item $i$:

    \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot \overrightarrow{\mathbf{z}}_{u,i}) \end{aligned}\]

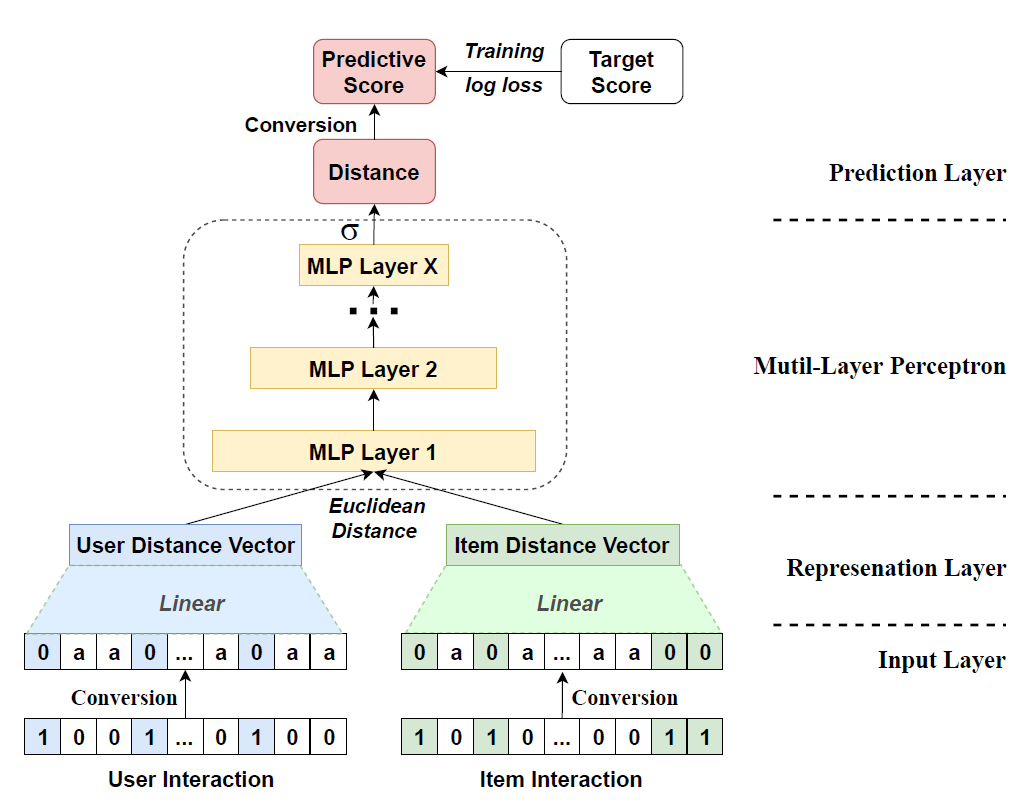
MeFL

• Conversion Transformation:

  \[\begin{aligned} x_{u,i} &=\alpha\left(1-y_{u,i}\right) \end{aligned}\]
  • $y_{u,i} \in \mathbf{Y}$ is Implicit Feedback
  • $\alpha$ is Distance Factor

• History Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u} &= \mathbf{W} \cdot \mathbf{X}_{u*}\\ \overrightarrow{\mathbf{q}}_{i} &= \mathbf{W} \cdot \mathbf{X}_{*i} \end{aligned}\]

• Calculate Euclidean Distance:

  \[\begin{aligned} \text{dist}[\overrightarrow{\mathbf{p}}_{u}, \overrightarrow{\mathbf{q}}_{i}] &= \Vert \overrightarrow{\mathbf{p}}_{u} - \overrightarrow{\mathbf{q}}_{i} \Vert_{2}\\ &= \sqrt{\sum_{k=1}^{K}{(p_{k}^{(u)} - q_{k}^{(i)})^{2}}} \end{aligned}\]

• predictive vector of user $u$ and item $i$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \text{MLP}_{\text{ReLU}}(\text{dist}[\overrightarrow{\mathbf{p}}_{u}, \overrightarrow{\mathbf{q}}_{i}]) \end{aligned}\]

• if use MeFL as a single prediction module:

  • compute distance:

    \[\begin{aligned} \hat{d}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot \overrightarrow{\mathbf{z}}_{u,i}) \end{aligned}\]

  • convert distance to matching score:

    \[\begin{aligned} \hat{y}_{u,i} &= 1 - \frac{\hat{d}_{u,i}}{\alpha} \end{aligned}\]

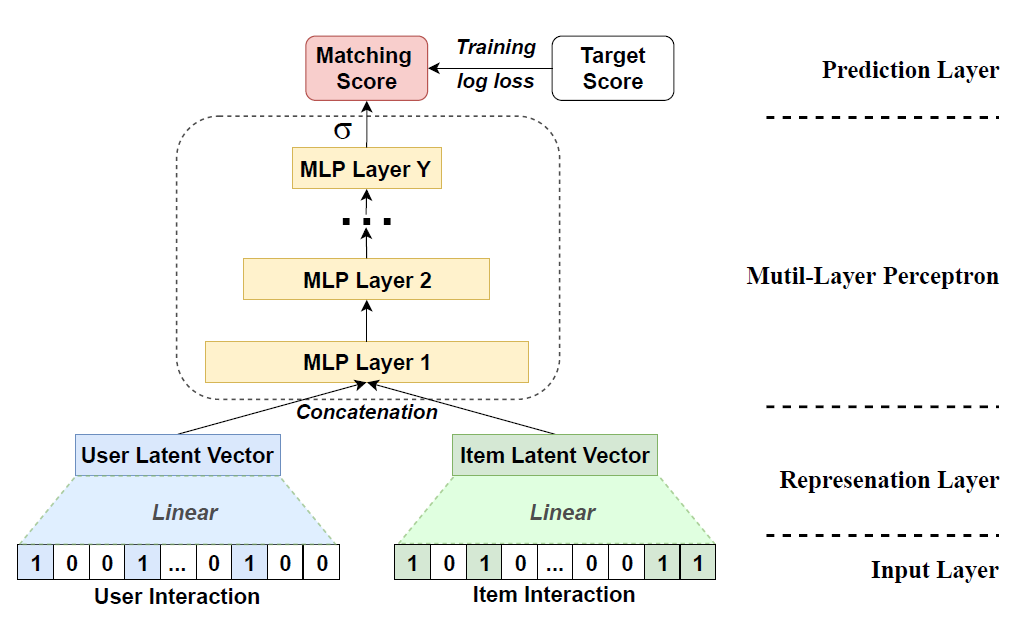
MaFL

• History Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \mathbf{W} \cdot \mathbf{Y}_{u*}\\ \overrightarrow{\mathbf{v}}_{i} &= \mathbf{W} \cdot \mathbf{Y}_{*i} \end{aligned}\]

• predictive vector of user $u$ and item $i$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{u}}_{u} \oplus \overrightarrow{\mathbf{v}}_{i}) \end{aligned}\]

• if use MaFL as a single prediction module:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot \overrightarrow{\mathbf{z}}_{u,i}) \end{aligned}\]