Dual Embedding based Latent Factor Model

Embedding Type

---

• 아이디 임베딩(ID Embedding)
  • Embedding user and item identifiers into a low-dimensional vector space
  • 사용자의 고유한 선호 정보나 아이템의 고유한 특징 정보를 반영한 표현을 도출함
  • 사용자와 아이템의 맥락 정보가 부족하여 행동 패턴이나 구매 패턴을 반영하기 어려움
• 히스토리 임베딩(History Embedding)
  • Generate each user and item expressions based on past interaction history
  • 사용자의 행동 패턴이나 아이템의 구매 패턴을 반영한 표현을 도출함
  • 사용자와 아이템을 상호간에 의존하여 표현하므로 고유 정보를 보존하기 어려움

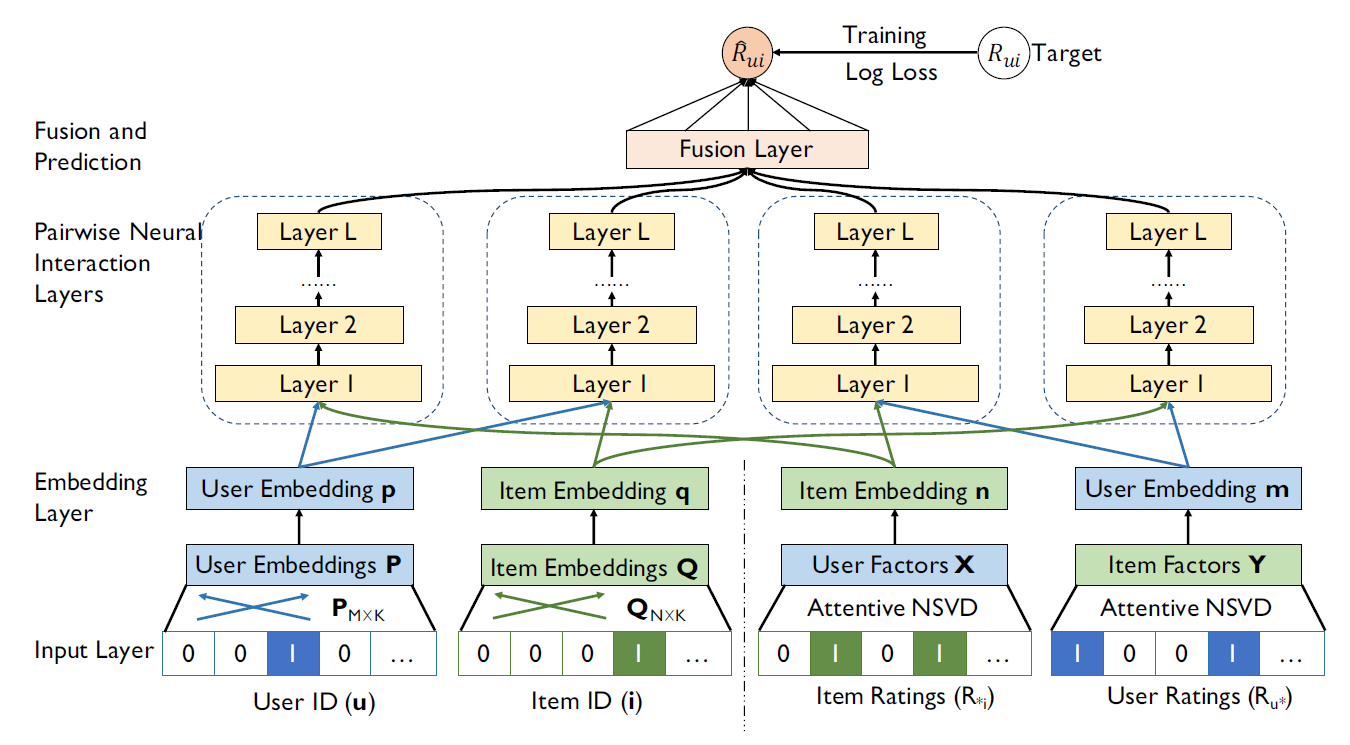
DNCF

---

• 문제 의식: 아이디 임베딩(ID Embedding)과 히스토리 임베딩(History Embedding)의 분리로 인한 표현력의 제약
  • DELF 는 아이디 임베딩과 히스토리 임베딩을 분리하여 매칭 함수 학습을 수행함
  • 각 표현이 서로의 표현력을 보완하거나 강화하지 못함
• DNMF(Deep Neural Matrix Factorization): 아이디 임베딩과 히스토리 임베딩을 결합한 하나의 표현을 생성하여 NeuMF 의 표현력을 강화하는 앙상블 모형
  • He, G., Zhao, D., & Ding, L.
    (2021).
    Dual-embedding based neural collaborative filtering for recommender systems.
    arXiv preprint arXiv:2102.02549.
• Components
  • DGMF: Dual-Embedding based Generalized Matrix Factorization
  • DMLP: Dual-Embedding based Multi-Layer Perceptron
  • DNMF: DGMF & DMLP Ensemble

Notation

---

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\mathbf{Y} \in \mathbb{R}^{M \times N}$: user-item interaction matrix
• $\overrightarrow{\mathbf{p}}_{u} \in \mathbb{R}^{K}$: user ID embedding vector
• $\overrightarrow{\mathbf{q}}_{i} \in \mathbb{R}^{K}$: item ID embedding vector
• $\overrightarrow{\mathbf{m}}_{u} \in \mathbb{R}^{K}$: user history embedding vector
• $\overrightarrow{\mathbf{n}}_{i} \in \mathbb{R}^{K}$: item history embedding vector
• $\overrightarrow{\mathbf{u}}_{u}$: user embedding combination vector
• $\overrightarrow{\mathbf{v}}_{i}$: item embedding combination vector
• $\overrightarrow{\mathbf{z}}_{u,i}$: predictive vector of user $u$ and item $i$
• $\hat{y}_{u,i}$: interaction probability of user $u$ and item $i$

How to Modeling

---

• DNMF is DGMF & DMLP Ensemble

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot [\overrightarrow{\mathbf{z}}_{u,i}^{\text{(DGMF)}} \oplus \overrightarrow{\mathbf{z}}_{u,i}^{\text{(DMLP)}}] + \overrightarrow{\mathbf{b}}) \end{aligned}\]

DGMF

• ID Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u} &=\text{Emb}(u)\\ \overrightarrow{\mathbf{q}}_{i} &=\text{Emb}(i) \end{aligned}\]

• History Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{m}}_{u} &=\frac{1}{\sqrt{\vert \mathcal{R}_{u}^{+} \setminus \{i\} \vert}}\mathbf{W} \cdot \mathbf{Y}_{u*}\\ \overrightarrow{\mathbf{n}}_{i} &=\frac{1}{\sqrt{\vert \mathcal{R}_{i}^{+} \setminus \{u\} \vert}}\mathbf{W} \cdot \mathbf{Y}_{*i} \end{aligned}\]

• Embedding Combination:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \text{Agg}(\overrightarrow{\mathbf{p}}_{u}, \overrightarrow{\mathbf{m}}_{u})\\ \overrightarrow{\mathbf{v}}_{i} &= \text{Agg}(\overrightarrow{\mathbf{q}}_{i}, \overrightarrow{\mathbf{n}}_{i}) \end{aligned}\]
  • element-wise sum
  • element-wise mean
  • concatenation
  • attention

• Predictive Vector of user $u$ and item $i$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \overrightarrow{\mathbf{u}}_{u} \odot \overrightarrow{\mathbf{v}}_{i} \end{aligned}\]

• If use DGMF as a single prediction module:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot \overrightarrow{\mathbf{z}}_{u,i} + \overrightarrow{\mathbf{b}}) \end{aligned}\]

DMLP

• ID Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u} &=\text{Emb}(u)\\ \overrightarrow{\mathbf{q}}_{i} &=\text{Emb}(i) \end{aligned}\]

• History Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{m}}_{u} &=\frac{1}{\sqrt{\vert \mathcal{R}_{u}^{+} \setminus \{i\} \vert}}\mathbf{W} \cdot \mathbf{Y}_{u*}\\ \overrightarrow{\mathbf{n}}_{i} &=\frac{1}{\sqrt{\vert \mathcal{R}_{i}^{+} \setminus \{u\} \vert}}\mathbf{W} \cdot \mathbf{Y}_{*i} \end{aligned}\]

• Embedding Combination:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \overrightarrow{\mathbf{p}}_{u} \oplus \overrightarrow{\mathbf{m}}_{u}\\ \overrightarrow{\mathbf{v}}_{i} &= \overrightarrow{\mathbf{q}}_{i} \oplus \overrightarrow{\mathbf{n}}_{i} \end{aligned}\]

• Predictive Vector of user $u$ and item $i$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{u}}_{u} \oplus \overrightarrow{\mathbf{v}}_{i}) \end{aligned}\]

• If use DMLP as a single prediction module:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot \overrightarrow{\mathbf{z}}_{u,i} + \overrightarrow{\mathbf{b}}) \end{aligned}\]