Exponential and Extension

Exponential

---

• 지수 분포(Exponential Distribution): 포아송 과정에서 두 사건 사이 대기시간을 나타내는 분포

  \[\begin{aligned} X\sim\mathrm{Exp}(\lambda),\quad X\ge0 \end{aligned}\]
  • $\lambda>0$: 단위시간당 평균 사건 발생률로서 스케일 파라미터의 역수

• probability density function:

  \[\begin{aligned} p(x\mid\lambda) &=\lambda\exp{-\lambda x} \end{aligned}\]

• moment generating function:

  \[\begin{aligned} M_{X}(t) &=\mathbb{E}_{p(x)}\left[\exp{tX}\right]\\ &=\int_{0}^{\infty}{\exp{tx}\cdot\lambda\exp{-\lambda x}\mathrm{d}x}\\ &=\lambda\int_{0}^{\infty}{\exp{-(\lambda-t)x}\mathrm{d}x}\\ &=\frac{\lambda}{1-t},\quad \lambda>t \end{aligned}\]
  • $\mathbb{E}\left[X\right]=(\mathrm{d}/\mathrm{d}t)M_{X}(t)\vert_{t=0}=1/\lambda$
  • $\mathbb{E}\left[X^{2}\right]=(\mathrm{d}^{2}/\mathrm{d}t^{2})M_{X}(t)\vert_{t=0}=2/\lambda^{2}$
  • $\mathrm{Var}\left[X\right]=\mathbb{E}\left[X^{2}\right]-\mathbb{E}\left[X\right]^{2}=1/\lambda^{2}$

• canonical form:

  \[\begin{aligned} p(x) &=\lambda\exp{\left[-\lambda x\right]}\\ &=\exp{\left[\log\lambda\right]}\cdot\exp{\left[-\lambda x\right]}\\ &=1\cdot\exp{\left[-\lambda x-\left(-\log{\lambda}\right)\right]} \end{aligned}\]
  • $T(x)=x$
  • $\eta(\theta)=-\lambda$
  • $A(\eta)=-\log{\lambda}$
  • $h(x)=1$

Gamma

---

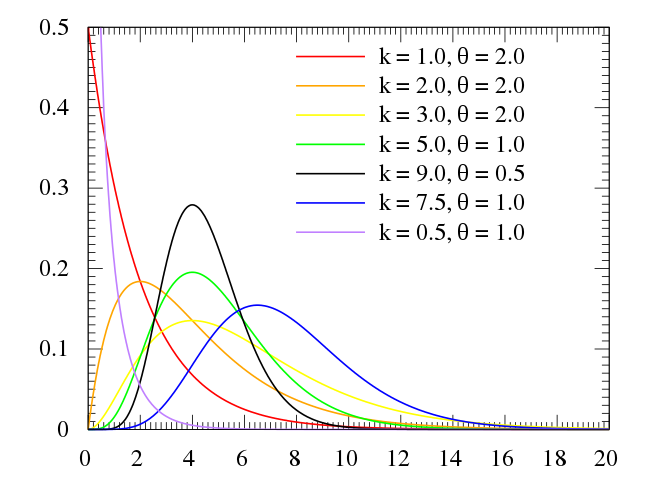
• 감마 분포(Gamma Distribution): 지수 분포의 사건 발생 횟수를 일반화한 분포로서, 양의 누적 물리량을 나타내는 분포

  \[\begin{gathered} T_{k}=X_{1}+\cdots+X_{k}\quad\mathrm{for}\quad X_{i}\overset{\text{i.i.d}}{\sim}\mathrm{Exp}(\lambda)\\ \Downarrow\\ T_{k}\sim\mathrm{Gamma}(\alpha=k,\beta=\lambda),\quad T_{k}>0 \end{gathered}\]
  • $\alpha>0$: 사건 누적 횟수로서 형상 파라미터
  • $\beta>0$: 사건 단위당 평균 물리량으로서 스케일 파라미터의 역수

• probability density function:

  \[p(x\mid\alpha,\beta) =\frac{\beta^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}\exp{-\beta x}\]

• gamma function:

  \[\begin{aligned} \Gamma(\alpha) &=\int_{0}^{\infty}{x^{\alpha-1}\exp{-x}\mathrm{d}x},\quad \alpha>0\\ &=(\alpha-1)!\quad\mathrm{s.t.}\quad\alpha\in\mathbb{Z} \end{aligned}\]

• moment generating function:

  \[\begin{aligned} M_{X}(t) &=\mathbb{E}_{p(x)}\left[\exp{tX}\right]\\ &=\int_{0}^{\infty}{\exp{tx}\frac{\beta^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}\exp{-\beta x}\mathrm{d}x}\\ &=\frac{\beta^{\alpha}}{\Gamma(\alpha)}\int_{0}^{\infty}{x^{\alpha-1}\exp{-(\beta-t) x}\mathrm{d}x},\quad t<\beta\\ \\ u &:=(\beta-t)x\\ \mathrm{d}x &:=\frac{1}{\beta-t}\mathrm{d}u\\ \\ \therefore M_{X}(t) &=\frac{\beta^{\alpha}}{\Gamma(\alpha)}\int_{0}^{\infty}{\left(\frac{u}{\beta-t}\right)^{\alpha-1}\exp{-u}\frac{1}{\beta-t}\mathrm{d}u}\\ &=\left(\frac{\beta}{\beta-t}\right)^{\alpha}\frac{1}{\Gamma(\alpha)}\underbrace{\int_{0}^{\infty}{u^{\alpha-1}\exp{-u}\mathrm{d}u}}_{=:\Gamma(\alpha)}\\ &=\left(\frac{\beta}{\beta-t}\right)^{\alpha} \end{aligned}\]
  • $\mathbb{E}\left[X\right]=(\mathrm{d}/\mathrm{d}t)M_{X}(t)\vert_{t=0}=\alpha/\beta$
  • $\mathbb{E}\left[X^{2}\right]=(\mathrm{d}^{2}/\mathrm{d}t^{2})M_{X}(t)\vert_{t=0}=\alpha(\alpha+1)/\beta^{2}$
  • $\mathrm{Var}\left[X\right]=\mathbb{E}\left[X^{2}\right]-\mathbb{E}\left[X\right]^{2}=\alpha/\beta^{2}$

• canonical form:

  \[\begin{aligned} p(x) &=\frac{\beta^{\alpha}}{\Gamma(\alpha)}x^{\alpha-1}\exp{-\beta x}\\ &=\exp{\left[(\alpha-1)\log{x}-\beta x+\alpha\log{\beta}-\log{\Gamma(\alpha)}\right]}\\ &=1\cdot\exp{\left[\begin{pmatrix}\alpha-1\\-\beta\end{pmatrix}^{T}\begin{pmatrix}\log{x}\\x\end{pmatrix}-(\log{\Gamma(\alpha})-\alpha\log{\beta})\right]} \end{aligned}\]
  • $T(x)=\log{x},x$
  • $\eta(\theta)=\alpha-1,-\beta$
  • $A(\eta)=\log{\Gamma(\alpha)}-\alpha\log{\beta}$
  • $h(x)=1$