FPMC

Previous Research

---

• 잠재요인 모형(Latent Factor Model) : 사용자 개인화 추천 알고리즘

  \[\mathbf{R}_{M \times N} \approx \mathbf{P}_{M \times K} \cdot \mathbf{Q}_{N \times K}^{T}\]

• 마르코프 체인 모형(Markov Chain Model) : 비개인화 순차 추천 알고리즘

  \[\alpha_{i,j} \in \mathcal{A} = P\left(S_{t}=j \mid S_{t-1}=i\right)\]
  • $\alpha_{i,j} \in \mathcal{A}$ : 상태 $i$ 에서 $j$ 로 전이될 확률로서, 시점 $t-1$ 에서 아이템 $i$ 를 선택했을 때, $t$ 에서 $j$ 를 선택할 가능성
  • $S_{t}$ : 시점 $t$ 의 상태로서, 해당 시점에 선택된 아이템

Concept

---

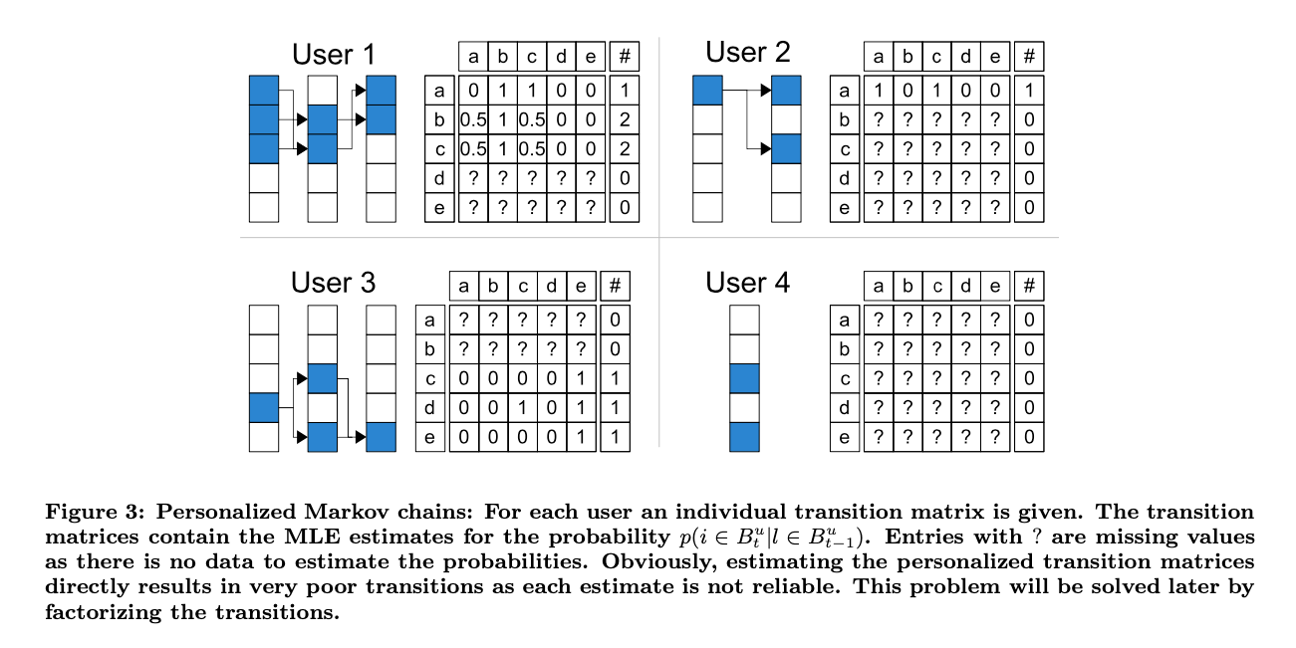
• FPMC(Factorizing Personalized Markov Chains) : 개별 사용자마다 장바구니 아이템 전이행렬을 모델링하는 사용자 개인화 순차 추천 알고리즘

  

  • 사용자 \(u\) 가 이전 시점 \(t-1\) 에서 장바구니 \(\Omega^{(u)}(t-1)\) 에 아이템 \(l\) 을 담았을 때, 현재 시점 \(t\) 에서 장바구니 \(\Omega^{(u)}(t)\) 에 아이템 \(i\) 를 담을 확률

    \[\alpha^{(u)}_{l,i} = P\left(S_{t} = i \in \Omega^{(u)}(t) \mid S_{t-1} = l \in \Omega^{(u)}(t-1)\right)\]

  • 사용자 $u$ 의 이전 시점 장바구니 내역이 $\Omega^{(u)}(t-1)$ 로 주어졌을 때, 현재 시점에서 아이템 $i$ 를 장바구니에 담을 확률

    \[\begin{aligned} x^{(u)}_{i}(t) &= P\left(S_{t} = i \in \Omega^{(u)}(t) \mid S_{t-1} = \Omega^{(u)}(t-1)\right)\\ &= \frac{1}{\vert \Omega^{(u)}(t-1) \vert}\sum_{l \in \Omega^{(u)}(t-1)}{\alpha^{(u)}_{l,i}} \end{aligned}\]

• 문제점 : 과도한 학습파라미터 갯수

  

  \[\mathcal{A} \in \mathbb{R}^{\vert U \vert \times \vert I \vert \times \vert L \vert}\]
  • 모든 학습파라미터를 추론하는 것은 비효율적일 수 있음
  • 모든 학습파라미터를 추론하기에 관측치가 충분하지 않을 수 있음
  • 모든 학습파라미터를 직접 추론하는 것은 과적합을 유발할 수 있음

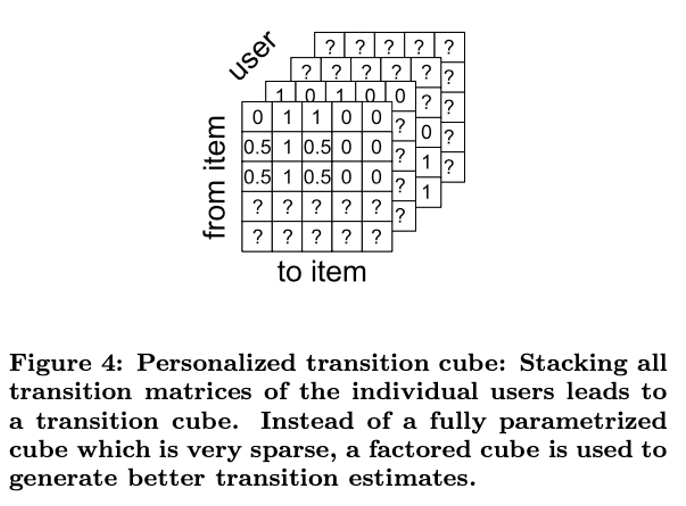
• 해법 : 행렬 분해를 활용한 전이큐브 추론

  

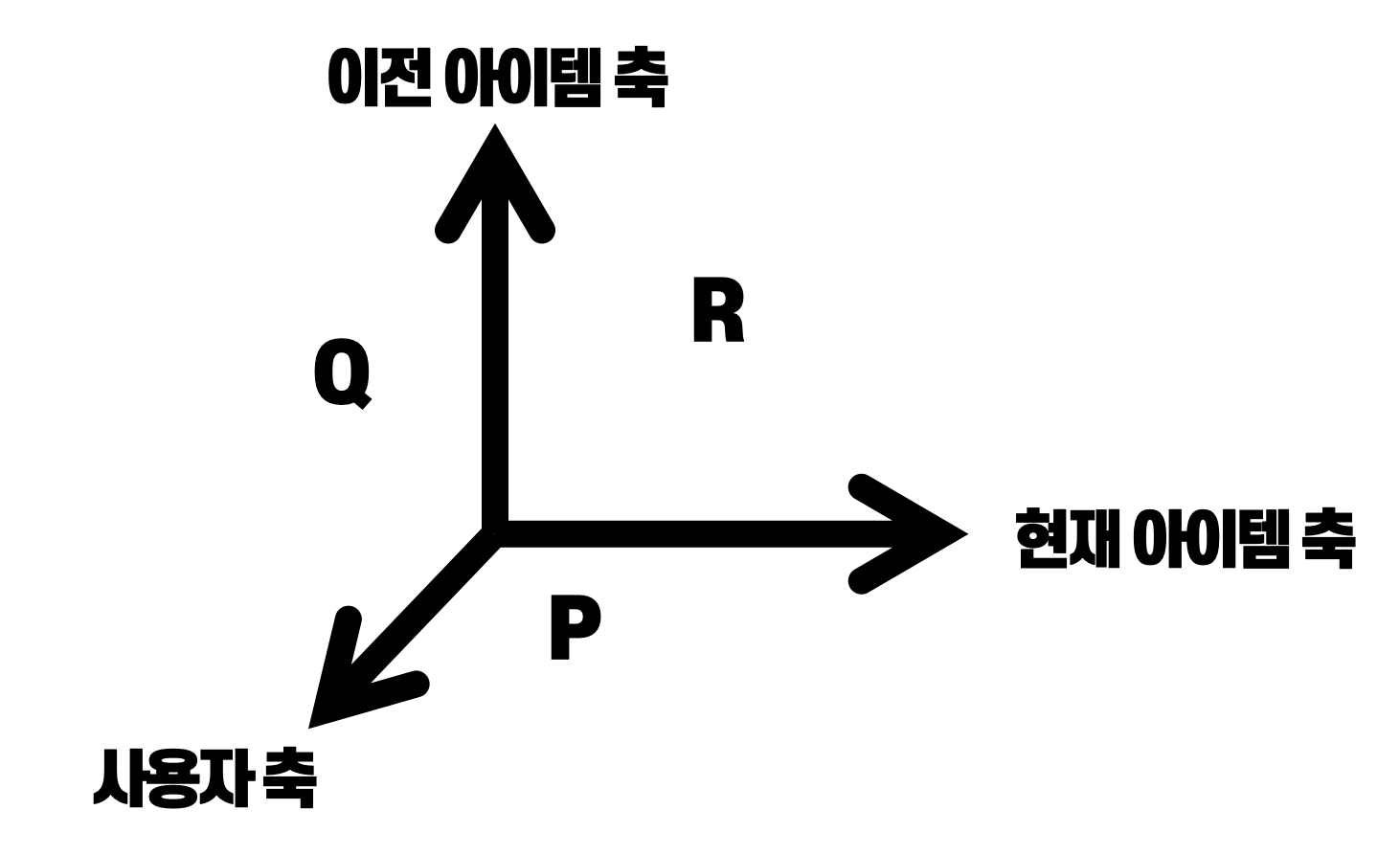
  \[\mathcal{A}_{\vert U \vert \times \vert I \vert \times \vert L \vert} \approx \mathbf{P}_{\vert U \vert \times \vert I \vert} + \mathbf{Q}_{\vert U \vert \times \vert L \vert} + \mathbf{R}_{\vert I \vert \times \vert L \vert}\]

  • $\mathbf{P}$ : 사용자들이 현재 시점 장바구니에 담긴 아이템들과 상호작용한 정보를 정리한 행렬

    \[\mathbf{P}_{\vert U \vert \times \vert I \vert} \approx \mathbf{V}^{(U;I)}_{\vert U \vert \times K} \cdot \mathbf{V}^{(I;U)}_{\vert I \vert \times K}\]

  • $\mathbf{Q}$ : 사용자들이 이전 시점 장바구니에 담긴 아이템들과 상호작용한 정보를 정리한 행렬

    \[\mathbf{Q}_{\vert U \vert \times \vert L \vert} \approx \mathbf{V}^{(U;L)}_{\vert U \vert \times K} \cdot \mathbf{V}^{(L;U)}_{\vert L \vert \times K}\]

  • $\mathbf{R}$ : 이전 시점 장바구니에 담긴 아이템들과 현재 시점 장바구니에 담긴 아이템들 간 관계 정보를 정리한 행렬

    \[\mathbf{R}_{\vert I \vert \times \vert L \vert} \approx \mathbf{V}^{(I;L)}_{\vert I \vert \times K} \cdot \mathbf{V}^{(L;I)}_{\vert L \vert \times K}\]

How to Modeling

---

• 행렬 분해를 활용한 전이 큐브 추정

  \[\mathcal{A} \approx \underbrace{\mathbf{V}^{(U;I)} \cdot \mathbf{V}^{(I;U)}}_{\approx \mathbf{P}_{\vert U \vert \times \vert I \vert}} + \underbrace{\mathbf{V}^{(U;L)} \cdot \mathbf{V}^{(L;U)}}_{\approx \mathbf{Q}_{\vert U \vert \times \vert L \vert}} + \underbrace{\mathbf{V}^{(I;L)} \cdot \mathbf{V}^{(L;I)}}_{\approx \mathbf{R}_{\vert I \vert \times \vert L \vert}}\]

• 추정된 전이 확률

  \[\alpha_{l,i}^{(u)} \approx \underbrace{\langle \overrightarrow{\mathbf{v}}^{(U;I)}_{u}, \overrightarrow{\mathbf{v}}^{(I;U)}_{i} \rangle}_{\approx\mathbf{P}_{u,i}} + \underbrace{\langle \overrightarrow{\mathbf{v}}^{(U;L)}_{u}, \overrightarrow{\mathbf{v}}^{(L;U)}_{l} \rangle}_{\approx\mathbf{Q}_{u,l}} + \underbrace{\langle \overrightarrow{\mathbf{v}}^{(I;L)}_{i}, \overrightarrow{\mathbf{v}}^{(L;I)}_{l} \rangle}_{\approx\mathbf{R}_{i,l}}\]

• 사용자 u가 현재 시점의 장바구니에 아이템 i를 담을 확률 도출

  \[\begin{aligned} x_{i}^{(u)}(t) &= \frac{1}{\vert \Omega^{(u)}(t-1) \vert}\sum_{l \in \Omega^{(u)}(t-1)}{\alpha^{(u)}_{l,i}}\\ &\approx \frac{1}{\vert \Omega^{(u)}(t-1) \vert}\sum_{l \in \Omega^{(u)}(t-1)}{\langle \overrightarrow{\mathbf{v}}^{(U;I)}_{u}, \overrightarrow{\mathbf{v}}^{(I;U)}_{i} \rangle + \langle \overrightarrow{\mathbf{v}}^{(U;L)}_{u}, \overrightarrow{\mathbf{v}}^{(L;U)}_{l} \rangle + \langle \overrightarrow{\mathbf{v}}^{(I;L)}_{i}, \overrightarrow{\mathbf{v}}^{(L;I)}_{l} \rangle}\\ &= \langle \overrightarrow{\mathbf{v}}^{(U;I)}_{u}, \overrightarrow{\mathbf{v}}^{(I;U)}_{i} \rangle + \frac{1}{\vert \Omega^{(u)}(t-1) \vert}\sum_{l \in \Omega^{(u)}(t-1)}{\langle \overrightarrow{\mathbf{v}}^{(U;L)}_{u}, \overrightarrow{\mathbf{v}}^{(L;U)}_{l} \rangle + \langle \overrightarrow{\mathbf{v}}^{(I;L)}_{i}, \overrightarrow{\mathbf{v}}^{(L;I)}_{l} \rangle} \end{aligned}\]

Pair-Wise Optimization

---

• 쌍별 최적화(Pair-Wise Optimization) : 타깃 시점에서 장바구니에 실제로 담겨 있는 아이템들이($i \in \Omega^{(u)}(t)$), 실제로 담겨 있지 않은 아이템들보다($j \notin \Omega^{(u)}(t)$) 장바구니에 담길 가능성이 높게 측정되도록 학습 과정 설계

Log Joint Posterior Probability

• 우도 함수(Liklihood Function) : 현재 시점에서 사용자 $u$ 의 장바구니에 실제로 담겨 있는 아이템 $i$ 가 장바구니에 담길 것이라 추론할 가능성이, 실제로 담겨 있지 않은 아이템 $j$ 가 장바구니에 담길 것이라 추론할 가능성보다 더 높을 확률

  \[P\left(i>^{(u)}_{t}j \mid \Theta \right) = \sigma\left(x_{i}^{(u)}(t) - x_{j}^{(u)}(t)\right)\]
  • $x_{i}^{(u)}(t)$ : 현재 시점에서 사용자 $u$ 의 장바구니에 실제로 담겨 있는 아이템 $i$ 에 대하여, 해당 아이템이 장바구니에 담길 것이라 추론할 가능성
  • $x_{j}^{(u)}(t)$ : 현재 시점에서 사용자 $u$ 의 장바구니에 실제로 담겨 있지 않은 아이템 $j$ 에 대하여, 해당 아이템이 장바구니에 담길 것이라 추론할 가능성

• 사후 확률(Posterior Probability) : 쌍별 데이터 $i \in \Omega$, $j \notin \Omega$ 가 주어졌을 때 특정 학습파라미터 조합이 실현될 확률

  \[\pi\left(\Theta \mid i>^{(u)}_{t}j \right) \propto \sigma\left(x_{i}^{(u)}(t) - x_{j}^{(u)}(t)\right) \cdot P\left(\Theta \right)\]

• 공동 사후 확률(Joint Posterior Probability) : 주어진 데이터 세트 하 특정 학습파라미터 조합이 실현될 확률

  \[\Pi\left(\Theta \mid \mathcal{D}\right) = \prod_{u \in U}{\prod_{\Omega^{(u)}(t) \in \Omega^{(u)}}{\prod_{i \in \Omega^{(u)}(t)}{\prod_{j \notin \Omega^{(u)}(t)}{\sigma\left(x_{i}^{(u)}(t) - x_{j}^{(u)}(t)\right) \cdot P\left(\Theta \right)}}}}\]

• 로그 공동 사후 확률(Log Joint Posterior Probability)

  \[\ln{\Pi\left(\Theta \mid \mathcal{D}\right)} = \sum_{u \in U}{\sum_{\Omega^{(u)}(t) \in \Omega^{(u)}}{\sum_{i \in \Omega^{(u)}(t)}{\sum_{j \notin \Omega^{(u)}(t)}{\sigma\left(x_{i}^{(u)}(t) - x_{j}^{(u)}(t)\right) + \lambda_{\Theta} \Vert \Theta \Vert^{2}}}}}\]

Optimization

• 불변성에 근거한 목적 함수 단순화

  \[\begin{aligned} x_{i}^{(u)}(t) &\approx \langle \overrightarrow{\mathbf{v}}^{(U;I)}_{u}, \overrightarrow{\mathbf{v}}^{(I;U)}_{i} \rangle + \frac{1}{\vert \Omega^{(u)}(t-1) \vert}\sum_{l \in \Omega^{(u)}(t-1)}{\cancel{\langle \overrightarrow{\mathbf{v}}^{(U;L)}_{u}, \overrightarrow{\mathbf{v}}^{(L;U)}_{l} \rangle} + \langle \overrightarrow{\mathbf{v}}^{(I;L)}_{i}, \overrightarrow{\mathbf{v}}^{(L;I)}_{l} \rangle}\\ &\approx \langle \overrightarrow{\mathbf{v}}^{(U;I)}_{u}, \overrightarrow{\mathbf{v}}^{(I;U)}_{i} \rangle + \frac{1}{\vert \Omega^{(u)}(t-1) \vert}\sum_{l \in \Omega^{(u)}(t-1)}{\langle \overrightarrow{\mathbf{v}}^{(I;L)}_{i}, \overrightarrow{\mathbf{v}}^{(L;I)}_{l} \rangle} \end{aligned}\]

  현재 시점 장바구니에 담긴 아이템 $i$ 와 담기지 않은 아이템 $j$ 간 쌍별 최적화 학습 시, 즉, 두 아이템 간 장바구니에 담길 가능성의 격차를 최대화하는 과정에서는 사용자가 이전 시점 장바구니에 담긴 아이템 $l$ 과 상호작용한 정보는 실질적으로 활용되지 않으므로 계산 효율성을 위해 제거해도 무방함

• 최적화

  \[\mathbf{V}^{(U;I)}, \mathbf{V}^{(I;U)}, \cancel{\mathbf{V}^{(U;L)}}, \cancel{\mathbf{V}^{(L;U)}}, \mathbf{V}^{(I;L)}, \mathbf{V}^{(L;I)} \mid K = \text{arg} \max_{\Theta}{\ln{\Pi\left(\Theta \mid \mathcal{D}\right)}}\]