Fourier Analysis (1) Fourier Series

Euler’s Formula

---

• 오일러 공식(Euler’s Formula): 복소 지수 함수와 삼각함수의 관계를 나타내는 공식

  • 복소 지수 함수의 테일러 급수:

    \[\begin{aligned} \exp{i\theta} = \sum_{n=0}^{\infty}{\frac{(i\theta)^{n}}{n!}} = \sum_{k=0}^{\infty}{\frac{(i\theta)^{2k}}{(2k)!}} + \sum_{k=0}^{\infty}{\frac{(i\theta)^{2k+1}}{(2k+1)!}} \end{aligned}\]

  • $n=2k$:

    \[\begin{aligned} (i\theta)^{2k} &= (-1)^{k}\theta^{2k}\\ \therefore \sum_{k=0}^{\infty}{\frac{(i\theta)^{2k}}{(2k)!}} &=\sum_{k=0}^{\infty}{\frac{(-1)^{k}\theta^{2k}}{(2k)!}}\\ &=: \cos{\theta} \end{aligned}\]

  • $n=2k+1$:

    \[\begin{aligned} (i\theta)^{2k+1} &= i(-1)^{k}\theta^{2k+1}\\ \therefore \sum_{k=0}^{\infty}{\frac{(i\theta)^{2k+1}}{(2k+1)!}} &= i\sum_{k=0}^{\infty}{\frac{(-1)^{k}\theta^{2k+1}}{(2k+1)!}}\\ &=: i\sin{\theta} \end{aligned}\]

  • 오일러 공식:

    \[\begin{aligned} \therefore \exp{i\theta} &= \cos{\theta} + i\sin{\theta} \end{aligned}\]

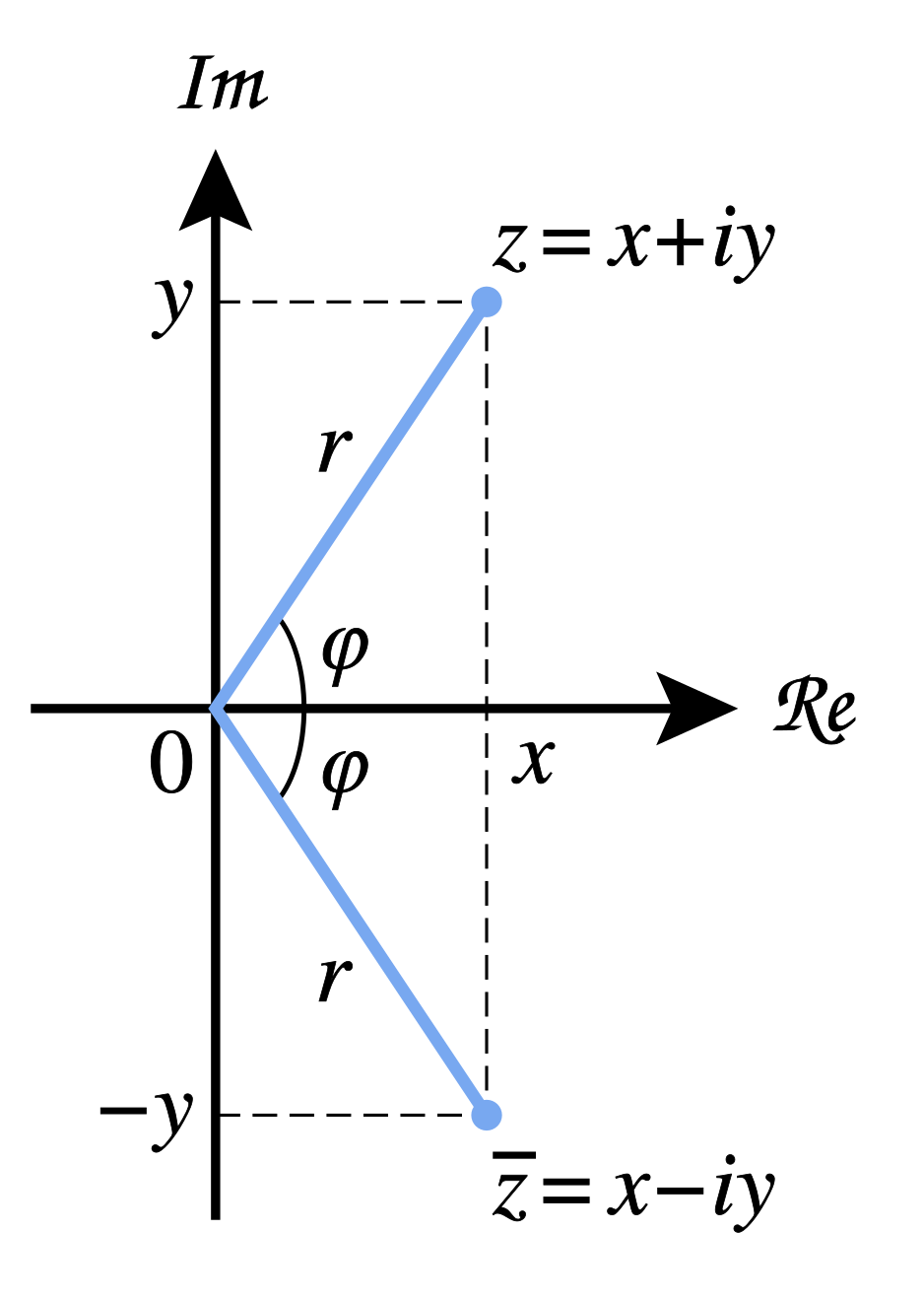
• 복소평면(Complex Plane): 복소수 \(Z=x+i \cdot y\) 는 실수축 기저 \(\mathbf{e}_{X}=\begin{bmatrix}1 \\ 0\end{bmatrix}\) 와 허수축 기저 \(\mathbf{e}_{Y}=\begin{bmatrix}0 \\ 1\end{bmatrix}\) 로 구성된 벡터 공간 \(\mathbb{R}^{2}\) 상의 벡터 \(\mathbf{v}_{Z}=\mathbf{e}_{X}x + \mathbf{e}_{Y}y\) 로 표현될 수 있으며, 이때 이 벡터 공간을 복소평면이라 정의함

  

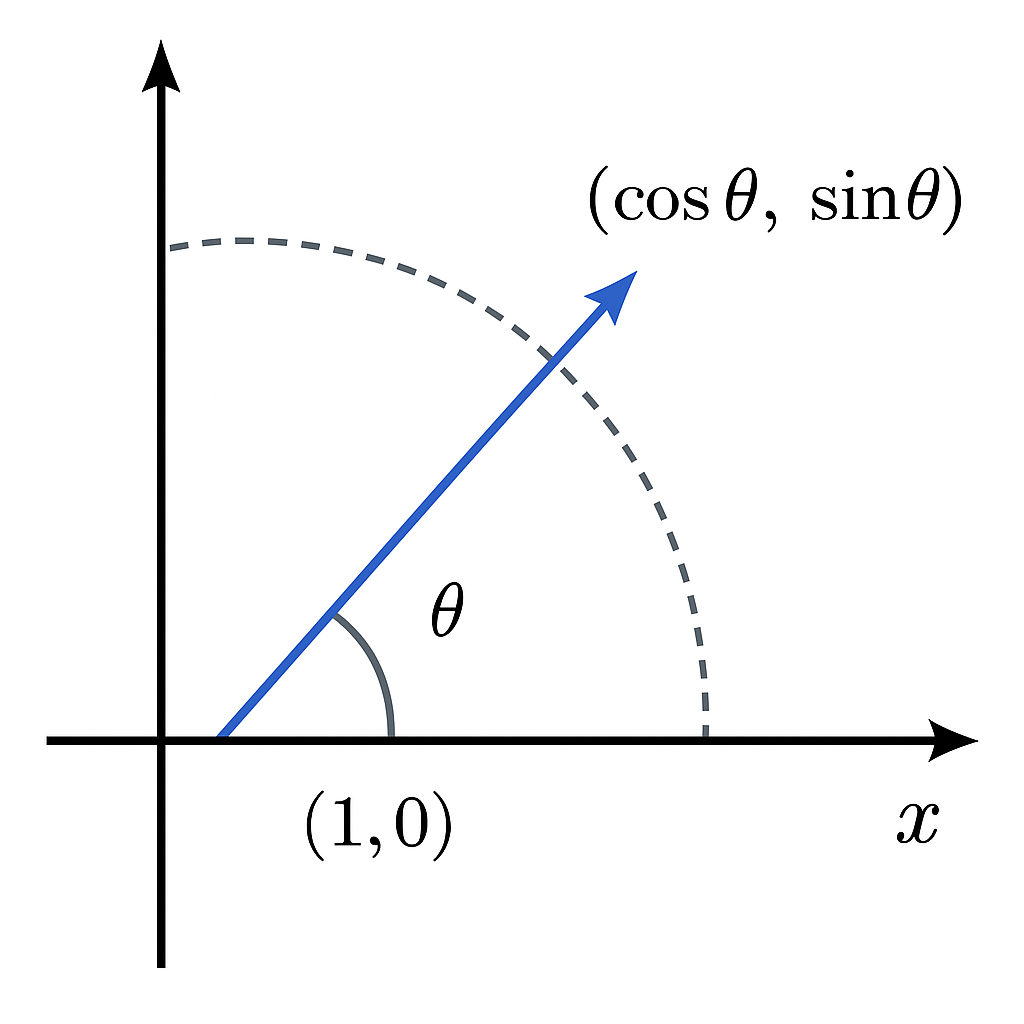
• 회전 변환(Rotation): $X$ 축 기준 반시계 방향으로 벡터를 회전시키는 선형 변환

  

  • 회전 변환 행렬(Rotation Matrix):

    \[\begin{aligned} R(\theta) &:= \begin{bmatrix} \cos{\theta} & -\sin{\theta}\\ \sin{\theta} & \cos{\theta} \end{bmatrix} \end{aligned}\]

  • 실수부 기저 벡터를 회전 변환하면:

    \[\begin{aligned} R(\theta)\mathbf{e}_{X} = 1 \cdot \begin{bmatrix} \cos{\theta}\\ \sin{\theta} \end{bmatrix} + 0 \cdot \begin{bmatrix} -\sin{\theta}\\ \cos{\theta} \end{bmatrix} \leftrightarrow \cos{\theta} + i \sin{\theta} \end{aligned}\]

  • 따라서 복소 지수 함수는 복소 평면 상의 벡터를 실수 축 기준 반시계 방향으로 $\theta$ 만큼 회전 변환함:

    \[\begin{aligned} \exp{i\theta} &= \cos{\theta} + i\sin{\theta} \end{aligned}\]

Fourier Series

---

• 푸리에 급수(Fourier Series): 기저 주기가 $T$ 인 주기 함수 $X_{T}(t)$ 를 복소 지수 함수들의 선형 결합으로 근사하는 방법

  \[\begin{aligned} X_{T}(t) &= \cdots + a_{-1}\phi_{-1}(t) + a_{0} + a_{1}\phi_{1}(t) + \cdots\\ &= \sum_{k=-\infty}^{\infty}{a_{k}\phi_{k}(t)} \end{aligned}\]
  • $a_{k}$: 푸리에 계수(Fourier Coefficients)로서 $k$ 번째 복소 지수 함수의 영향력을 의미함

• 푸리에 기저 함수(Fourier Basis Function): 복소 지수 함수로서 이산적인 주파수 스펙트럼을 나타냄

  \[\begin{aligned} \phi_{k}(t) := \exp{i \omega_{k} t} = \cos{\omega_{k} t} + i \sin{\omega_{k} t} \end{aligned}\]
  • $\nu_{0}=1/T$ (Hz): 기본 주파수(Frequency)로서 초당 진동 횟수(Count)
  • $\nu_{k}=k \cdot \nu_{0}$ (Hz): 고조파(Harmonic Frequency)로서 기본 주파수 $\nu_{0}$ 의 정수 $k \in \mathbb{Z}$ 배 주파수
  • $\omega_{0}=2\pi \nu_{0}$ (rad/s): 기본 각주파수(Angular Frequency)로서 초당 회전 각속도(Angle)
  • $\omega_{k}=2\pi \nu_{k}$ (rad/s): 고조파 각주파수(Harmonic Angular Frequency)로서 기본 각주파수 $\omega_{0}$ 의 정수 $k \in \mathbb{Z}$ 배 주파수

• 기본 주파수를 $\nu_{0}$ 으로 취하는 푸리에 기저 함수들은 상호 직교함:

  \[\begin{aligned} \left<\phi_{m}(t),\phi_{n}(t)\right> &= \int_{t \in T}{\phi_{m}(t)\phi_{n}^{*}(t)\mathrm{d}t}\\ &=\int_{t \in T}{\exp{\left[i m \omega_{0} t\right]}\exp{\left[-i n \omega_{0} t\right]}\mathrm{d}t}\\ &= \int_{t \in T}{\exp{\left[i (m-n) \omega_{0} t\right]}\mathrm{d}t}\\ &= \begin{cases}\begin{aligned} T \quad &\mathrm{if} \quad m = n\\ 0 \quad &\mathrm{if} \quad m \ne n \end{aligned}\end{cases} \end{aligned}\]

  • $m = n$:

    \[\begin{aligned} \int_{t \in T}{\exp{\left[i (m-n) \omega_{0} t\right]}\mathrm{d}t} = \int_{t \in T}{1 \mathrm{d}t} = T \end{aligned}\]

  • $m \ne n$:

    \[\begin{aligned} \int_{t \in T}{\exp{\left[i (m-n) \omega_{0} t\right]}\mathrm{d}t} &= \frac{1}{i(m-n)\omega_{0}}\left(\exp\left[i(m-n)\omega_{0}T\right]-1\right)\\ \\ \exp\left[i(m-n)\omega_{0}T\right] &= \exp\left[i 2\pi (m-n)\right] \quad (\because \omega_{0}T = 2\pi)\\ &= \underbrace{\cos{2\pi (m-n)}}_{=1} + i \cdot \underbrace{\sin{2\pi (m-n)}}_{=0}\\ &= 1 \quad \text{s.t.} \quad (m-n) \in \mathbb{Z}\\ \\ \therefore \int_{t \in T}{\exp{\left[i (m-n) \omega_{0} t\right]}\mathrm{d}t} &= 0 \end{aligned}\]

• 푸리에 계수(Fourier Coefficients): 주기가 $T$ 인 신호에서 $n$ 번째 고조파의 평균 기여도

  \[\begin{aligned} \left<X_{T}(t),\phi_{n}(t)\right> &= \int_{t \in T}{X_{T}(t)\phi_{n}^{*}(t)\mathrm{d}t}\\ &= \int_{t \in T}{\left(\sum_{k=-\infty}^{\infty}{a_{k}\phi_{k}(t)}\right)\phi_{n}^{*}(t)\mathrm{d}t}\\ &= \sum_{k=-\infty}^{\infty}{a_{k}\int_{t \in T}{\phi_{k}(t)\phi_{n}^{*}(t)\mathrm{d}t}}\\ &= a_{n}T + \sum_{k \ne n}{a_{k} \cdot 0}\\ &= a_{n}T\\ \\ \therefore a_{n} &= \frac{1}{T}\left<X_{T}(t),\phi_{n}(t)\right> \end{aligned}\]