Gaussian Process

Stochastic Process

---

• 확률적 과정(Stochastic Process)

  어떤 시점 혹은 위치 지표 $t$ 에 대하여 확률변수들의 집합 \(\{X_{t} \mid t \in T\}\) 이 주어졌을 때 이를 확률적 과정이라고 한다. 즉, 확률적 과정은 시간 또는 공간을 따라 변화하는 확률변수들의 집합으로서, 특정한 시점 또는 위치에서 확률변수가 결정된다. 이때 시간 또는 공간을 따라 확률변수가 변하는 양상은 특정한 확률적 패턴을 가질 수 있다.

• vs. Deterministic

  • 결정론적 과정(Deterministic Process) : 시스템의 상태가 주어지면 미래 상태가 항상 유일하게 결정되므로 동일한 초기 조건에서는 항상 동일한 경로(Trajectory)가 생성됨

    • EXAMPLE Deterministic Auto-Regressive Model

      \[\begin{aligned} X_{t} &= \beta + \sum_{i=1}^{p}{\alpha_{i} \cdot X_{t-i}} \end{aligned}\]

  • 확률적 과정(Stochastic Process) : 초기 조건이 동일하더라도 매 실행(Realization)마다 다른 경로(Trajectory)가 생성될 수 있음

    • EXAMPLE Auto-Regressive Model | Stochastic Error

      \[\begin{aligned} X_{t} = \beta + \sum_{i=1}^{p}{\alpha_{i} \cdot X_{t-i}} + \epsilon_{t}, \quad \epsilon_{t} \sim \mathcal{N}\left(0, \sigma^{2}\right) \end{aligned}\]

    • EXAMPLE Auto-Regressive Model | Stochastic Initial Variable

      \[\begin{aligned} X_{t} = \beta + \sum_{i=1}^{p}{\alpha_{i} \cdot X_{t-i}}, \quad X_{0} \sim \mathcal{N}\left(\mu, \sigma^{2}\right) \end{aligned}\]

• Stochastic Patterns

  • 독립 확률 과정(Independent Stochastic Process) : 각 포인트에서의 확률변수 $X_{t}$ 가 서로 독립인 확률 과정

    \[\begin{aligned} P\left(X_{t} \mid X_{t-1}, X_{t-2}, \cdots, X_{0}\right) = P\left(X_{t}\right) \end{aligned}\]

  • 마코프 과정(Markov Process) : 현재 상태 $X_{t}$ 가 주어졌을 때, 미래 상태 $X_{t+1}$ 는 과거 상태들과 독립이고 오직 현재 상태에만 의존하는 과정

    \[\begin{aligned} P\left(X_{t+1} \mid X_{t}, X_{t-1}, X_{t-2}, \cdots, X_{0}\right) = P\left(X_{t+1} \mid X_{t}\right) \end{aligned}\]

  • 정상 과정(Stationary Process) : 시간 혹은 공간에 따라 확률적으로 변화하는 패턴이 일정한 성질을 유지하는 과정

    \[\begin{aligned} X_{t} = \alpha \cdot X_{t-1} + \epsilon_{t}, \quad \epsilon_{t} \sim \mathcal{N}\left(0, \sigma^{2}\right) \end{aligned}\]

    • 확률변수 \(X_{t}\) 의 기대값이 일정함

      \[\text{E}\left[X_{t^{\forall}}\right]=\mu\]

    • 확률변수 \(X_{t}\) 의 변동성이 일정함

      \[\text{Var}\left[X_{t^{\forall}}\right]=\text{E}\left[\left(X_{t^{\forall}}-\mu\right)\right]=\sigma^{2}\]

    • $X_{t}$ 와 $X_{t+h}$ 의 관계가 시점 $t$ 자체가 아니라 시간 차이 $h$ 에만 의존함

      \[\text{Cov}\left[X_{t},X_{t+h}\right]=\text{E}\left[\left(X_{t}-\mu\right)\left(X_{t+h}-\mu\right)\right]=\gamma\left(h\right)\]

Non-Parametric Density Estimation

---

Non-Parametric Method

• 밀도(Density) : 데이터가 특정 구간에 존재할 확률

• 모수 추정(Parametric Estimation) : 데이터가 모수로써 정의되는 특정한 형태로 분포되었다고 가정하고, 소수의 모수를 추정함으로써 데이터 분포를 추정하는 방법

  • EXAMPLE Probability Density Estimation
    확률변수 $X$ 는 평균을 $\mu$, 분산을 $\sigma^{2}$ 으로 하는 가우시안 분포에 따라 분포되어 있음

    \[\begin{aligned} X \sim \mathcal{N}\left(\mu, \sigma^{2}\right) \end{aligned}\]

  • EXAMPLE Regression Analysis
    한국인 남성의 키($Y$)는 몸무게($X$)와 선형 관계에 있음

    \[\begin{aligned} Y = \alpha \cdot X + \beta \end{aligned}\]

• 비모수 추정(Non-Parametric Estimation) : 데이터가 특정한 형태로 분포되었다고 가정하지 않고, 주어진 데이터를 토대로 직접 추정하는 방법

  • Histogram Density Estimation
  • Kernel Density Estimation
  • k-Nearest Neighbors Density Estimation
  • Maximum Entropy Density Estimation
  • Regression-Based Density Estimation

KDE

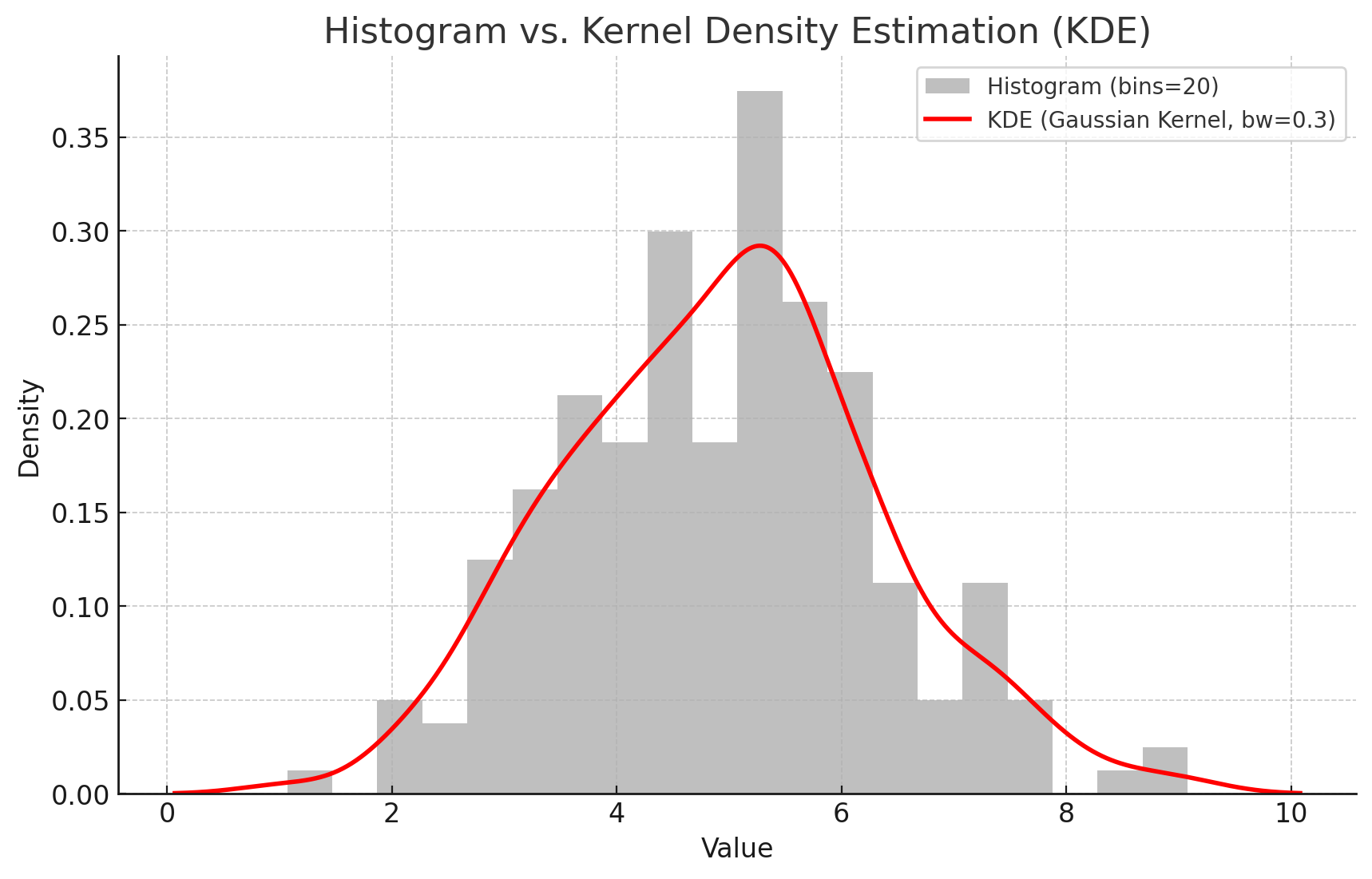
• 커널 밀도 추정(Kernel Density Estimation; KDE) : 각 데이터 주변에서 작은 확률 분포(Kernel)를 만든 후, 이를 합산하여 전체 밀도를 추정하는 방법

  

• 확률 밀도 함수(Probability Density Function)

  \[\begin{aligned} f(x) &= \frac{1}{h} \cdot \frac{1}{n} \cdot \sum_{i=1}^{n}{\mathcal{K}\left(\frac{x-x_{i}}{h}\right)} \end{aligned}\]
  • $n$ : 데이터 포인트 갯수
  • $x_{i}$ : 개별 데이터 포인트
  • $h$ : 밴드위스(Bandwidth)
  • $\mathcal{K}\left(\cdot\right)$ : 커널 함수(Kernel Function)

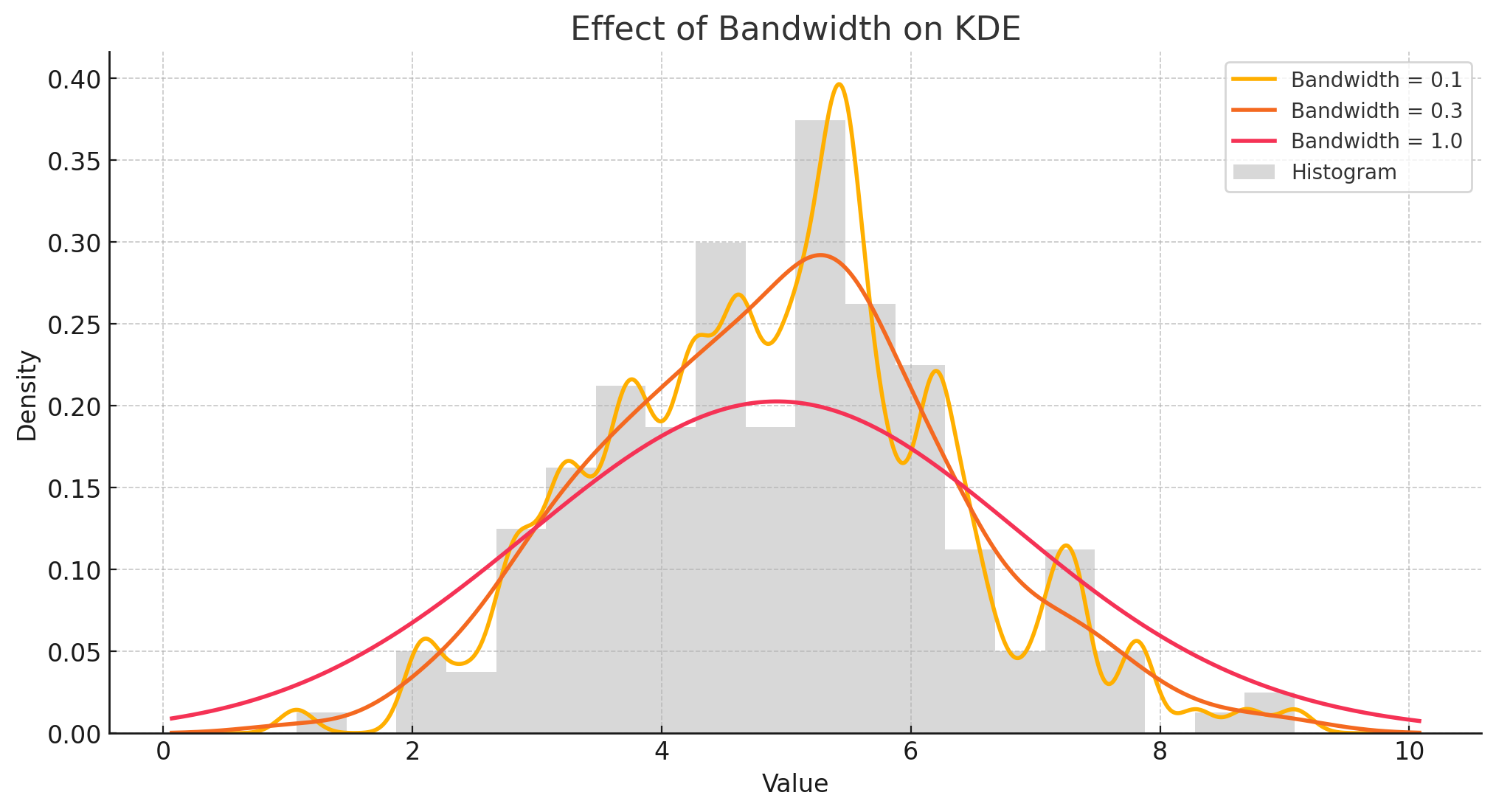
• 밴드위스(Bandwidth) : 커널의 너비를 조절하는 하이퍼파라미터로서, 값이 클수록 전역적 패턴을, 작을수록 국소적 패턴을 포착함

  

• 커널 함수(Kernel Function) : 특정 데이터 포인트 주변의 밀도를 조절하는 함수

  Name	Function
  Gaussian	\(\mathcal{K}(u) = \displaystyle\frac{1}{\sqrt{2\pi}} \exp\left(-\displaystyle\frac{u^2}{2}\right)\)
  Epanechnikov	\(\begin{aligned}\mathcal{K}(u)=\begin{cases}\displaystyle\frac{3}{4}(1-u^{2}), \quad &\text{if} \quad \vert u \vert \le 1 \\0, \quad &\text{otherwise}\end{cases}\end{aligned}\)
  Tophat	\(\begin{aligned}\mathcal{K}(u) = \begin{cases}\displaystyle\frac{1}{2}, \quad & \text{if} \quad \vert u \vert \le 1 \\0, \quad & \text{otherwise}\end{cases}\end{aligned}\)
  Logistic	\(\mathcal{K}(u) = \displaystyle\frac{1}{e^{u} + e^{-u} + 2}\)
  Silverman	\(\mathcal{K}(u) = \displaystyle\frac{1}{2} \cdot \exp\left(-\displaystyle\frac{\vert u \vert}{\sqrt{2}}\right) \cdot \cos\left(\displaystyle\frac{\vert u \vert}{\sqrt{2}}\right)\)
  Laplacian	\(\mathcal{K}(u) = \displaystyle\frac{1}{2} \cdot \exp(-\vert u \vert)\)

MVN

---

Multi-Variate Gaussian Distribution

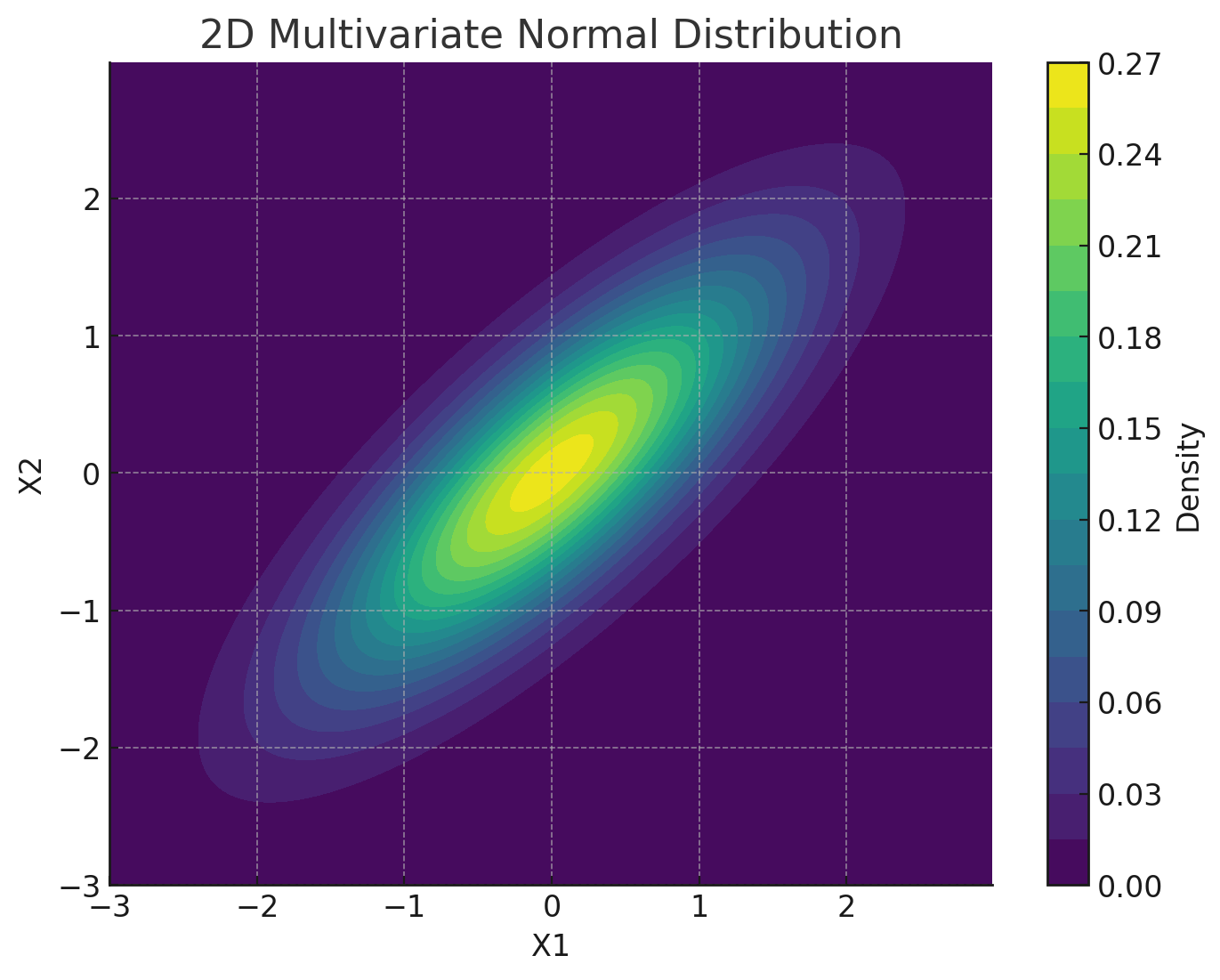
• 다변량 가우시안 분포(Multi-Variate Gaussian/Normal Distribution; MVN) : 유한 차원의 상관된 가우시안 확률변수 벡터에 대해 정의되는 가우시안 분포

  

• Definition

  \[\begin{aligned} \mathbf{X} \sim \mathcal{N}\left(\mu, \Sigma\right) \end{aligned}\]

  • \(\mathbf{X}= \begin{pmatrix}X_{1} & X_{2} & \cdots & X_{N}\end{pmatrix}^{T}\) : Multi-Variable

    • \(X_{i} \sim \mathcal{N}\left(\mu_{i}, \sigma_{i}^{2}\right)\) : The elements are random variables that follow individual Gaussian dist.
  • \(\mu=\begin{pmatrix}\mu_{1} & \mu_{2} & \cdots & \mu_{N}\end{pmatrix}^{T}\) : Mean Vector
  • \(\Sigma=\begin{pmatrix}\Sigma_{11} & \Sigma_{12} & \cdots & \Sigma_{1N}\\ \Sigma_{21} & \Sigma_{22} & \cdots & \Sigma_{2N}\\ \vdots & \vdots & \ddots & \vdots\\ \Sigma_{N1} & \Sigma_{N2} & \cdots & \Sigma_{NN} \end{pmatrix}\) : Covariance Matrix

• Probability Density Function

  \[\begin{aligned} f(\mathbf{X}) &= \frac{1}{(2\pi)^{n/2} \vert \Sigma \vert^{1/2}} \exp{\left[-\frac{1}{2}\underbrace{(\mathbf{X}-\mu)^{T}\Sigma^{-1}(\mathbf{X}-\mu)}_{\text{Mahalanobis Distance}}\right]} \end{aligned}\]

  • 마할라노비스 거리(Mahalanobis Distance) : 상관관계가 존재하는 다변량 데이터에서, 하나의 데이터 포인트가 특정 분포 혹은 군집에서 얼마나 떨어져 있는지를 측정하는 개념으로서, 단순 좌표 상의 거리뿐만 아니라 데이터 분포(분산-공분산 구조)를 반영하여 측정함

    \[\begin{aligned} D_{M}(x) &= \sqrt{(x-\mu)^{T}\Sigma^{-1}(x-\mu)} \end{aligned}\]
    • $\sqrt{(x-\mu)^{T}(x-\mu)}$ : 데이터 포인트와 특정 분포 중심점 간 편차로서 유클리드 거리
    • $\Sigma$ : 특정 분포의 공분산 행렬로서 데이터의 분산과 변수 간 상관관계를 포함하며, 이를 반영하여 방향성과 크기에 따라 거리를 조정함

Conditional Probability

\[\begin{aligned} Z_{2} \mid Z_{1} \sim \mathcal{N}\left(\mu_{2} + \Sigma_{21}\Sigma_{11}^{-1}(Z_{1}-\mu_{1}), \Sigma_{22}-\Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12}\right) \end{aligned}\]

• Multi-Variate Gaussian Dist.

  \[\begin{aligned} \mathbf{Z}=\begin{bmatrix}Z_{1} \\ Z_{2}\end{bmatrix} \sim \mathcal{N}\left(\begin{bmatrix}\mu_{1} \\ \mu_{2}\end{bmatrix}, \begin{bmatrix}\Sigma_{11} & \Sigma_{12}\\ \Sigma_{21} & \Sigma_{22}\end{bmatrix}\right) \end{aligned}\]

• Probability Density Function

  \[\begin{aligned} f(\mathbf{Z}) &= \frac{1}{(2\pi)^{n/2} \vert \Sigma \vert^{1/2}} \exp{\left[-\frac{1}{2}\underbrace{(\mathbf{Z}-\mu)^{T}\Sigma^{-1}(\mathbf{Z}-\mu)}_{\text{Mahalanobis Distance}}\right]} \end{aligned}\]

• Inv-Covariance Matrix

  \[\begin{aligned} \Sigma^{-1} &= \begin{bmatrix} \Sigma_{11}^{-1}+\Sigma_{11}^{-1}\Sigma_{12} \cdot \mathbf{M} \cdot \Sigma_{12}\Sigma_{11}^{-1} & -\Sigma_{11}^{-1}\Sigma_{12}\mathbf{M}\\ -\mathbf{M}\Sigma_{21}\Sigma_{11}^{-1} & \mathbf{M} \end{bmatrix} \end{aligned}\]
  • \(\mathbf{M}=\left(\Sigma_{22}-\Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12}\right)^{-1}\) : Schur Complement

• Exponent Formula Expansion

  \[\begin{aligned} (\mathbf{Z}-\mu)^{T}\Sigma^{-1}(\mathbf{Z}-\mu) &= \underbrace{(Z_{1}-\mu_{1})^{T}\Sigma_{11}^{-1}(Z_{1}-\mu_{1})}_{\text{Mahalanobis Distance of } Z_{1}}\\ &\quad + \underbrace{\Bigg[Z_{2}-\bigg\{\mu_{2}+\Sigma_{21}\Sigma_{11}^{-1}(Z_{1}-\mu_{1})\bigg\}\Bigg]^{T}\mathbf{M}\Bigg[Z_{2}-\bigg\{\mu_{2}+\Sigma_{21}\Sigma_{11}^{-1}(Z_{1}-\mu_{1})\bigg\}\Bigg]}_{\text{Conditional Mahalanobis Distance of }Z_{2} \mid Z_{1}} \end{aligned}\]

• Therefore,

  \[\begin{aligned} \text{E}\left[Z_{2} \mid Z_{1}\right] &= \mu_{2} + \Sigma_{21}\Sigma_{11}^{-1}(Z_{1}-\mu_{1})\\ \text{Var}\left[Z_{2} \mid Z_{1}\right] &= \Sigma_{22}-\Sigma_{21}\Sigma_{11}^{-1}\Sigma_{12} \end{aligned}\]

Gaussian Process

---

Gaussian Process

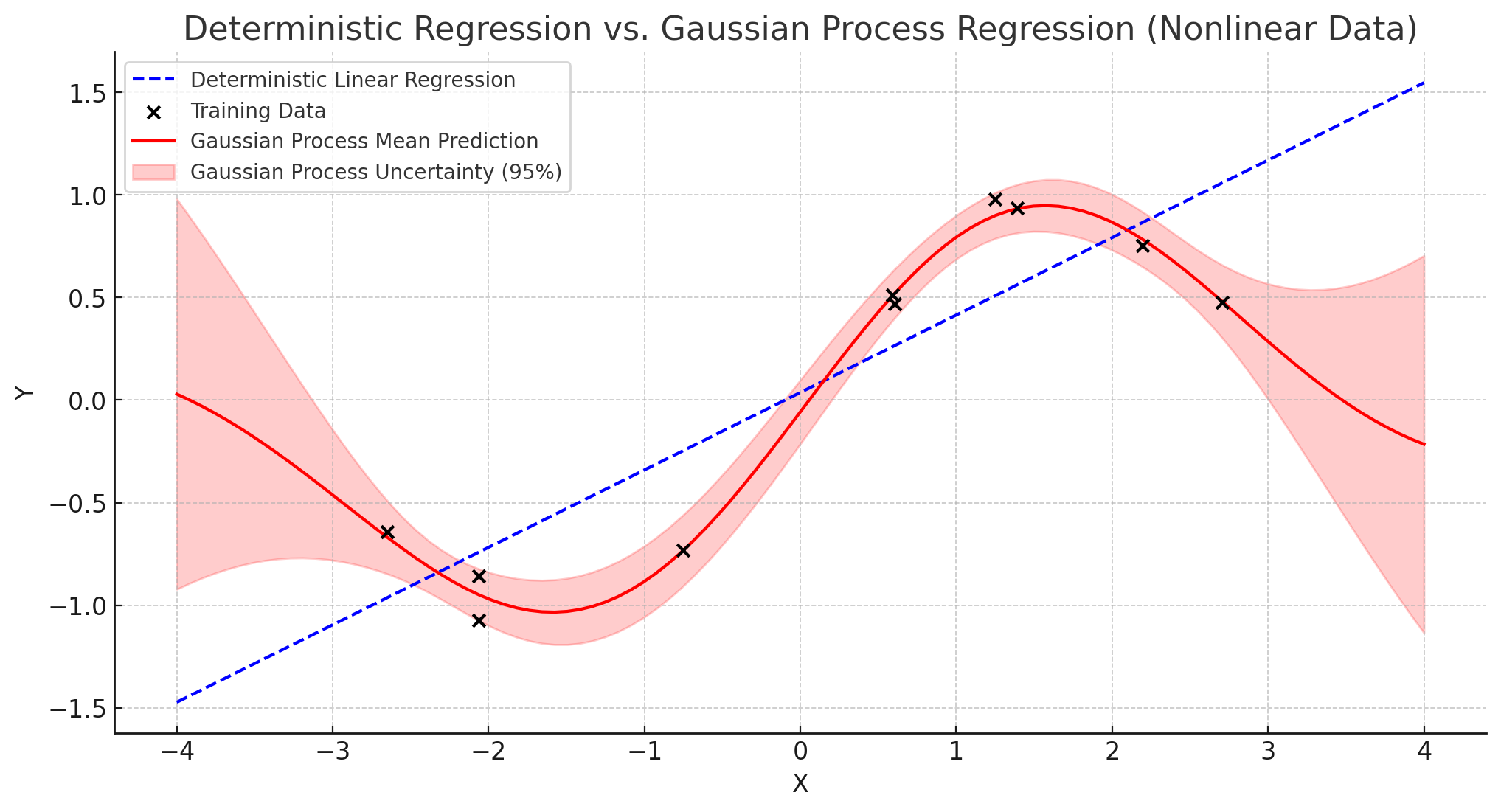
• 가우시안 프로세스(Gaussian Process; GP) : 무한 차원의 다변량 가우시안 분포를 가정하는 비모수 확률적 과정(Non-Parametric Stochastic Process)

  

• Definition

  함수 분포(Function Distribution)
  가우시안 프로세스는 각 입력값에 대한 관측치를 개별적인 확률변수로 간주하고 이를 무한 차원으로 확장함으로써 다변량 가우시안 분포의 개념을 함수 공간으로 확장함. 즉, 함수(설명변수와 반응변수 간 관계식)를 선험적으로 정의하지 않고 데이터를 통해 전체 함수 형태를 확률적으로 예측한다는 점에서, 가우시안 프로세스는 함수 자체를 하나의 확률변수로써 다루고, 이를 비모수 추정한다고 볼 수 있음.

  \[\begin{aligned} \mathcal{F} \sim \mathcal{GP}\left(\mu(X), \mathcal{K}(X, X^{\prime})\right) \end{aligned}\]
  • \(\mu(X)\) : 평균 함수(Mean Function)
  • \(\mathcal{K}(X, X^{\prime})\) : 공분산 함수(Covariance Function)

• 커널 함수(Kernel Function) : 두 입력 벡터 간 유사도 측정 함수로서 공분산 행렬을 구성함

  Name	Function
  Linear	\(\mathcal{K}\left(X,X^{\prime}\right) = X \cdot X^{\prime}\)
  Polynomial	\(\mathcal{K}\left(X,X^{\prime}\right) = \left(X \cdot X^{\prime} + \beta\right)^{d}\)
  RBF	\(\mathcal{K}\left(X,X^{\prime}\right) = \exp{\left[-\displaystyle\frac{\Vert X-X^{\prime} \Vert^{2}}{2\ell^{2}}\right]}\)
  Sigmoid	\(\mathcal{K}\left(X,X^{\prime}\right) = \text{tanh}\left(\alpha \cdot X \cdot X^{\prime} + \beta\right)\)
  Laplacian	\(\mathcal{K}\left(X,X^{\prime}\right) = \exp{\left[-\gamma \Vert X-X^{\prime} \Vert_{1}\right]}\)
  Exponential	\(\mathcal{K}\left(X,X^{\prime}\right) = \exp{\left[-\gamma \Vert X-X^{\prime} \Vert_{2}\right]}\)
  Matern	\(\mathcal{K}\left(X,X^{\prime}\right) = \displaystyle\frac{2^{1-\nu}}{\Gamma\left(\nu\right)} \cdot \left(\displaystyle\frac{\sqrt{2\nu} \Vert X-X^{\prime} \Vert}{\ell}\right)^{\nu} \cdot K_{\nu}\left(\displaystyle\frac{\sqrt{2\nu} \Vert X-X^{\prime} \Vert}{\ell}\right)\)
  Periodic	\(\mathcal{K}\left(X,X^{\prime}\right) = \exp\left[-2 \sin^2\left( \displaystyle\frac{\pi \vert X-X^{\prime} \vert}{p} \right) \Bigg/ \ell^2 \right]\)
  Rational Quadratic	\(\mathcal{K}\left(X,X^{\prime}\right) = \left( 1 + \displaystyle\frac{\vert X-X^{\prime} \vert^2}{2 \alpha \ell^2} \right)^{-\alpha}\)

  • 대칭성(Symmetry)

    \[\mathcal{K}\left(x,x^{\prime}\right)=\mathcal{K}\left(x^{\prime},x\right)\]

  • 양의 반정치성(Positive Semi-Definiteness, PSD)

    \[\sum_{i}\sum_{j}{\alpha_{i} \cdot \alpha_{j} \cdot \mathcal{K}\left(x_{i},x_{j}\right)} \ge 0\]

Bayesian Framework

• SUMMARY : 베이지안 프레임워크로써 이해했을 때 가우시안 프로세스는 기존 데이터 \((X,Y)\) 를 통해 새로운 입력 \(X^{*}\) 에 대한 함수 \(\mathcal{F}^{*}\) 를 사후확률로 갱신하는 과정으로 볼 수 있음

  \[\begin{aligned} p\left(\mathcal{F}^{*} \mid X, Y, X^{*}\right) &= \frac{p\left(Y \mid \mathcal{F}, X\right) \cdot p\left(\mathcal{F}^{*} \mid X^{*}\right)}{p\left(Y \mid X\right)} \end{aligned}\]
  • \(\mathcal{F}\) : Function Variable
  • \(\mathcal{F}^{*}\) : Function Variable Updated by New Observations
  • \(X,Y\) : Existing Observations
  • \(X^{*}\) : New Observations

• Prior Dist. : 새로운 입력을 관측하지 않은 상태에서 함수가 가질 수 있는 형태에 대한 정보는 기존에 관측되었던 값들로써 추론됨

  \[\begin{aligned} \mathcal{F}^{*} \mid X^{*} \sim \mathcal{GP}\left(\mu(X), \mathcal{K}(X, X^{\prime})\right) \end{aligned}\]

• Likelihood Function : 함수가 특정 형태일 때($\mathcal{F}$), 기존에 관측되었던 값은 함수 값을 중심으로 가우시안 분포 형태로 분포함

  \[\begin{aligned} Y &= \mathcal{F}\left(X\right) + \epsilon, \quad \epsilon \sim \mathcal{N}\left(0, \sigma_{N}^{2}\mathbf{I}\right)\\ &\Updownarrow\\ Y \mid \mathcal{F}, X &\sim \mathcal{N}\left(\mathcal{F}, \sigma_{N}^{2}\mathbf{I}\right) \end{aligned}\]

• Evidence : 기존에 관측되었던 값은 다변량 가우시안 분포를 따름

  \[\begin{aligned} Y \mid X \sim \mathcal{N}\left(\mu\left(X\right), \mathbf{K}_{N} + \sigma_{N}^{2}\mathbf{I}\right) \end{aligned}\]

Posterior Estimation

• MVN(Multi-Variate Normal Distribution) : 기존 데이터와 신규 데이터를 하나의 결합 가우시안 분포로 표현할 수 있음

  \[\begin{aligned} \begin{bmatrix}Y \\ \mathcal{F}^{*}\end{bmatrix} \sim \mathcal{N} \left(\begin{bmatrix}\mu(X) \\ \mu(X^{*})\end{bmatrix},\begin{bmatrix}\mathbf{K}_{N} + \sigma^{2}_{N}\mathbf{I} & \overrightarrow{\mathbf{k}}_{N}^{*} \\ \left(\overrightarrow{\mathbf{k}}_{N}^{*}\right)^{T} & \mathcal{K}(X^{*}, X^{*})\end{bmatrix}\right) \end{aligned}\]

  • Covariance vector between old and new:

    \[\begin{aligned} \overrightarrow{\mathbf{k}}_{n}^{*} = \begin{bmatrix}\mathcal{K}(X^{*},X_{1}) & \mathcal{K}(X^{*},X_{2}) & \cdots & \mathcal{K}(X^{*},X_{N})\end{bmatrix}^{T} \end{aligned}\]

• Posterior Dist. : 신규 데이터에 의해 갱신된 함수는 다시 가우시안 프로세스를 따름

  \[\begin{aligned} \mathcal{F}^{*} \mid X, Y, X^{*} \sim \mathcal{N}(\mu^{*}, (\sigma^{*})^{2}) \end{aligned}\]

  • Posterior Mean:

    \[\begin{aligned} \mu^{*}=\mu(X^{*}) + \overrightarrow{\mathbf{k}}_{N}^{*}(\mathbf{K}_{N}+\sigma^{2}_{N}\mathbf{I})^{-1}(Y-\mu(X)) \end{aligned}\]

  • Posterior Var.:

    \[\begin{aligned} (\sigma^{*})^{2} =\mathcal{K}(X^{*},X^{*})-\overrightarrow{\mathbf{k}}_{N}^{*}(\mathbf{K}_{N}+\sigma^{2}_{N}\mathbf{I})^{-1}\left(\overrightarrow{\mathbf{k}}_{N}^{*}\right)^{T} \end{aligned}\]