GPT

GPT

---

• 지피티(Generative Pre-trained Transformer; GPT) : 트랜스포머의 디코더 아키텍처를 기반으로 하여 다양한 텍스트 데이터로 사전 훈련된 자기회귀모형(Auto-Regressive Model)

  • 자기회귀모형(Auto-Regressive Model; AR) : 이전 출력값들을 참고하여 다음 출력값을 예측하는 모형

    \[\begin{aligned} X_{t} &= \beta + \sum_{i=1}^{p}{\alpha_{i} \cdot X_{t-i}} + \epsilon_{t} \end{aligned}\]
    • \(X_{t}\) : 현재 시점 출력값
    • \(X_{t-i}\) : 이전 시점 출력값
    • \(\alpha_{i}\) : 각 시점에 대한 가중치
    • \(\beta\) : 편향
    • \(\epsilon_{t}\) : 노이즈

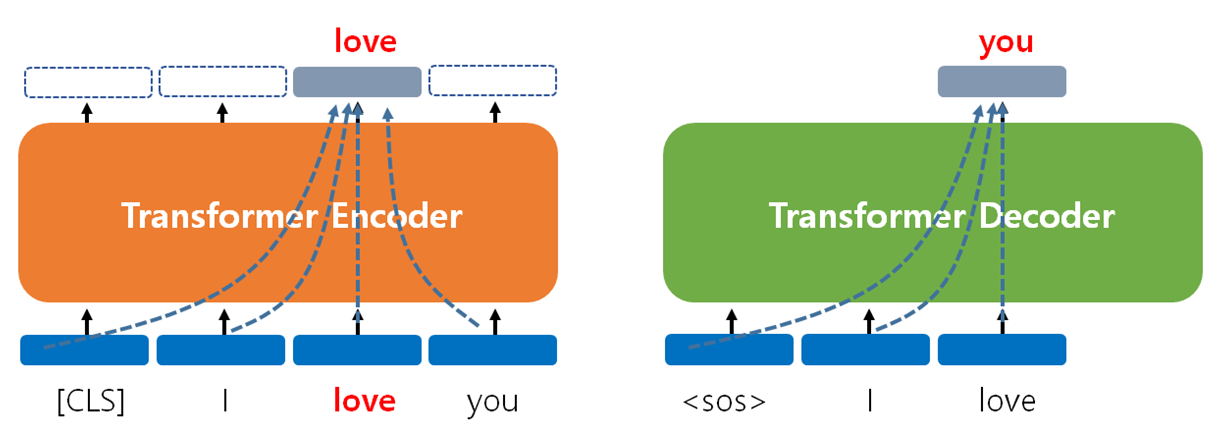
• vs. BERT

  

  	BERT	GPT
  Type	Masked Language Model	Auto-Regressive Model
  Task	Natural Language Understanding	Natural Language Generation
  Object	Predict Masked Word	Predict Next Word
  Direction	Bidirectional	Unidirectional
  Transformer	Encoder	Decoder

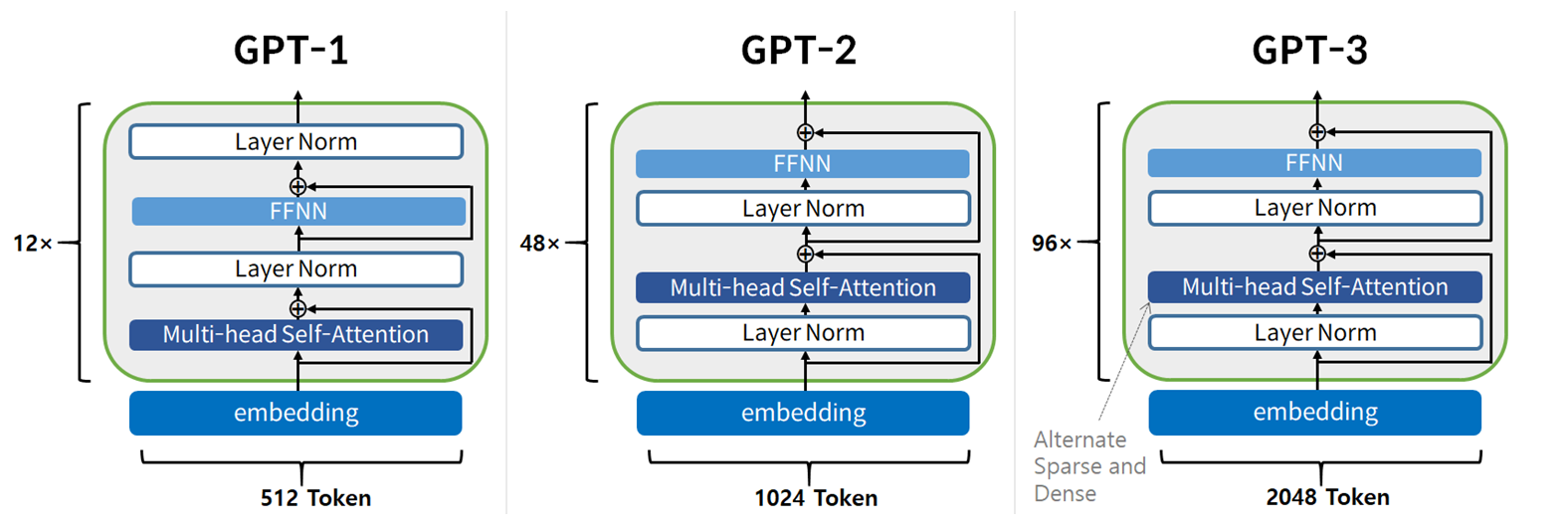
• Version

  

  	GPT-1	GPT-2	GPT-3
  Year	2018	2019	2020
  Embedding Dimension	768	1,024	12,288
  Decoder Layers	12	48	96
  Attention Heads	12	16	96
  Total Parameters	117M	1.5B~15B	175B
  Traning Data	BooksCorpus	OpenWebText	Common Crawl WebText2 Wikipedia BooksCorpus

Word Representation

---

• Unique(or Max) Number of Vector

  VECTOR	GPT-1	GPT-2	GPT-3
  Unique Tokens	40,000	50,257	50,257
  Max Seq	512	1,024	2,048

• Tokenization Method : BPE(Byte-Pair Encoding)

  • 단어를 문자(Byte) 단위로 쪼갠 후 가장 많이 등장하는 문자 쌍(Pair)을 병합하는 과정을 반복하여 최종 내부 단어(Sub-Word) 단위 토큰을 생성함

  • Split a Word into Bytes

    Word	Bytes
    low	[l, o, w]
    lower	[l, o, w, e, r]
    newest	[n, e, w, e, s, t]
    widest	[w, i, d, e, s, t]

  • Merge Pairs

    Pair	Count	Merge
    (l, o)	2	lo
    (o, w)	2	ow
    (e, s)	2	es
    (s, t)	2	st
    $\vdots$	$\vdots$	$\vdots$

  • Result

    Word	Sub-Word Tokens
    low	[lo, w]
    lower	[lo, w, er]
    newest	[ne, w, est]
    widest	[wi, d, est]

• Embedding

  \[\begin{aligned} \mathbf{x}_{i} &= \\mathbf{x}^{(i)}_{\text{TOKEN}} + \mathbf{x}^{(i)}_{\text{POS}} \end{aligned}\]

  • \(\mathbf{x}^{(i)}_{\text{TOKEN}}\) : Token Embedding

  • \(\mathbf{x}^{(i)}_{\text{POS}}\) : Position Embedding, Not Fixed But Learnable

Single Layer

---

\[\begin{aligned} \mathcal{X}^{(0)} &=\text{Embeddings}\left(\text{Tokens}\right)\\ \mathcal{H}^{(k)} &=\text{Layer-Norm}\Big[\text{Multi-Head}\left(\mathcal{X}^{(k)};\mathcal{M}\right) + \mathcal{X}^{(k)}\Big]\\ \mathcal{Y}^{(k)} &=\text{Layer-Norm}\Big[\text{FFN}\left(\mathcal{H}^{(k)}\right) + \mathcal{H}^{(k)}\Big] \end{aligned}\]

• $\mathcal{X}$ is Input Data of Single Layer, $\mathcal{Y}$ is Output Data of Single Layer
  • \(\mathcal{X}^{(k+1)}=\mathcal{Y}^{(k)}\) : Input Data of $k+1$ Decoder Layer is Output Data of $k$
  • Input Data of Initial Layer \(\mathcal{X}^{(0)}\) is Sum of Token Embedding & Position Embedding Vector
  • Output Data of Final Layer \(\mathcal{Z}=\mathcal{Y}^{(K)}\) is Output of Decoder Module

• \(\text{Multi-Head}\left(\mathcal{X}^{(k)};\mathcal{M}\right)\) : Multi-Head Masked Self Attention

  • $\mathcal{M}$ : Causal Mask(Upper-triangular mask)

• \(\text{FFN}\left(\mathcal{H}^{(k)}\right)\) : Feed-Forward Networks

  \[\begin{aligned} \text{FFN}\left(\mathcal{H}^{(k)}\right) &=\mathbf{W}^{(k)}_{2} \cdot \left(\text{ReLU}\left[\mathbf{W}^{(k)}_{1} \cdot \mathcal{H}^{(k)} + \mathbf{b}^{(k)}_{1}\right]\right) + \mathbf{b}^{(k)}_{2} \end{aligned}\]
  • $\mathbf{W}^{(k)}_{1} \in \mathbb{R}^{M \times 4d}$ : Dimension Expansion to four times the Dimension of the Embedding Vector
  • $\mathbf{W}^{(k)}_{2} \in \mathbb{R}^{M \times d}$ : Dimension Reduction to Embedding Vector Dimension

---

Sourse

• https://wikidocs.net/184363