Gaussian

definition

---

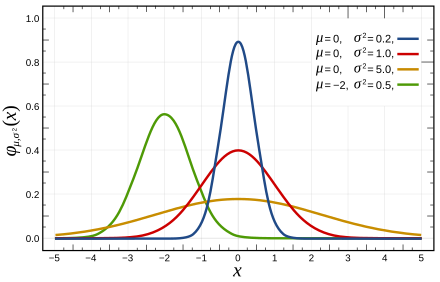
• 가우시안 분포(Gaussian Distribution): 독립적인 무작위 충격들이 누적되어 나타나는 연속 실수값을 나타내는 분포

  \[X\sim\mathcal{N}(\mu,\sigma^{2})\]
  • $\mu$: 평균 위치로서 위치 파라미터
  • $\sigma^{2}$: 분산으로서 스케일 파라미터

• probability density function:

  \[p(x\mid\mu,\sigma^{2}) =\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp{\left[-\frac{(x-\mu)^{2}}{2\sigma^{2}}\right]}\]

• moment generating function:

  \[\begin{aligned} M_{X}(t) &=\mathbb{E}_{p(x)}\left[\exp{tX}\right]\\ &=\int_{-\infty}^{\infty}{\exp{tx}\cdot\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp{\left[-\frac{(x-\mu)^{2}}{2\sigma^{2}}\right]}\mathrm{d}x}\\ &=\frac{1}{\sqrt{2\pi\sigma^{2}}}\int_{-\infty}^{\infty}{\exp{\left[tx-\frac{(x-\mu)^{2}}{2\sigma^{2}}\right]}\mathrm{d}x}\\ \\ tx-\frac{(x-\mu)^{2}}{2\sigma^{2}} &=-\frac{1}{2\sigma^{2}}x^{2}+\left(\frac{\mu}{\sigma^{2}}+t\right)x-\frac{\mu^{2}}{2\sigma^{2}}\\ &=-\frac{\left[x-(\mu+\sigma^{2}+t)\right]^{2}}{2\sigma^{2}}+\mu t+\frac{\sigma^{2}t^{2}}{2}\\ &=-\frac{\left(x-\mu^{\prime}\right)^{2}}{2\sigma^{2}}+\mu t+\frac{\sigma^{2}t^{2}}{2}\\ \\ \therefore M_{X}(t) &=\frac{1}{\sqrt{2\pi\sigma^{2}}}\int_{-\infty}^{\infty}{\exp{\left[\mu t+\frac{\sigma^{2}t^{2}}{2}\right]}\cdot\exp{\left[-\frac{(x-\mu^{\prime})^{2}}{2\sigma^{2}}\right]}\mathrm{d}x}\\ &=\exp{\left[\mu t+\frac{\sigma^{2}t^{2}}{2}\right]}\cdot\underbrace{\frac{1}{\sqrt{2\pi\sigma^{2}}}\int_{-\infty}^{\infty}{\exp{\left[-\frac{(x-\mu^{\prime})^{2}}{2\sigma^{2}}\right]}\mathrm{d}x}}_{=1}\\ &=\exp{\left[\mu t+\frac{\sigma^{2}t^{2}}{2}\right]} \end{aligned}\]
  • $\mathbb{E}\left[X\right]=(\mathrm{d}/\mathrm{d}t)M_{X}(t)\vert_{t=0}=\mu$
  • $\mathbb{E}\left[X^{2}\right]=(\mathrm{d}^{2}/\mathrm{d}t^{2})M_{X}(t)\vert_{t=0}=\mu^{2}+\sigma^{2}$
  • $\mathrm{Var}\left[X\right]=\mathbb{E}\left[X^{2}\right]-\mathbb{E}\left[X\right]^{2}=\sigma^{2}$

• canonical form ($\tau=1/\sigma^{2}$):

  \[\begin{aligned} p(x) &=\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp{\left[-\frac{(x-\mu)^{2}}{2\sigma^{2}}\right]}\\ &=\sqrt{\frac{\tau}{2\pi}}\exp{\left[-\frac{\tau}{2}(x-\mu)^{2}\right]}\\ &=\frac{1}{\sqrt{2\pi}}\exp{\left[\begin{pmatrix}-(1/2)\tau\\\mu\tau\end{pmatrix}^{T}\begin{pmatrix}x^{2}\\x\end{pmatrix}-\frac{1}{2}(\mu^{2}\tau-\log{\tau})\right]} \end{aligned}\]
  • $T(x)=x^{2},x$
  • $\eta(\theta)=-(1/2)\tau,\mu\tau$
  • $A(\eta)=(1/2)(\mu^{2}\tau-\log{\tau})$
  • $h(x)=1/\sqrt{2\pi}$

conjugate prior

---

• gaussian model:

  \[X\mid\tau\sim\mathcal{N}(0,\tau^{-1})\]

• canonical form:

  \[\begin{aligned} p(x\mid\tau) &=\sqrt{\frac{\tau}{2\pi}}\exp{\left[-\frac{\tau}{2}x^{2}\right]}\\ &=\frac{1}{\sqrt{2\pi}}\exp{\left[-\frac{1}{2}\tau x^{2}-\left(-\frac{1}{2}\log{\tau}\right)\right]} \end{aligned}\]
  • $T(x)=x^{2}$
  • $\eta(\theta)=-(1/2)\tau$
  • $A(\eta)=-(1/2)\log{\tau}$
  • $h(x)=1/\sqrt{2\pi}$

• prior of $\eta$:

  \[\begin{aligned} p(\eta) &\propto \exp\left[\alpha\cdot\eta(\theta)-\beta\cdot A(\eta)\right]\\ &=\exp{\left[\alpha\cdot\eta-\beta\cdot\left(-\frac{1}{2}\log{[-2\eta]}\right)\right]}\\ &=(-2\eta)^{\beta/2}\cdot\exp{\alpha\eta} \end{aligned}\]

• change of variables $\eta\to\tau$:

  \[\begin{aligned} p_{\tau}(\tau)\mathrm{d}\tau &=p_{\eta}(\eta)\mathrm{d}\eta\\ \therefore p_{\tau}(\tau) &=p_{\eta}\left(-\frac{1}{2}\tau\right)\left\vert\frac{\mathrm{d}\eta}{\mathrm{d}\tau}\right\vert\\ &=(\tau)^{\beta/2}\cdot\exp{\left[-\frac{\alpha}{2}\tau\right]}\cdot\frac{1}{2}\\ &=\frac{1}{2}\tau^{(\beta/2 + 1)-1}\exp{\left[-\frac{\alpha}{2}\tau\right]}\\ &\approx\mathrm{Gamma}\left(\frac{\beta}{2}+1,\frac{\alpha}{2}\right) \end{aligned}\]

• Therefore, the precision of the Gaussian distribution $1/\sigma^{2}$, the reciprocal of the variance, follows a gamma distribution. Here, each parameter of the gamma distribution represents (1) the number of virtual samples and (2) the precision scale.

  \[1/\sigma^{2}\sim\mathrm{Gamma}(\alpha,\beta)\]

sample variance distribution

---

• gaussian model:

  \[\begin{aligned} X\sim\mathcal{N}\left(\mu,\sigma^{2}\right),\quad\text{$\mu$ is known} \end{aligned}\]

• jeffreys prior of $\sigma^{2}$:

  \[\begin{aligned} p\left(\sigma^{2}\right)\propto \frac{1}{\sigma^{2}} \end{aligned}\]

• likelihood of $\sigma^{2}$:

  \[\begin{aligned} p\left(x_{1},\cdots,x_{k}\mid\sigma^{2}\right) &=\prod_{i=1}^{k}{p(x_{i}\mid\sigma^{2})}\quad(\because x_{i}\perp x_{j})\\ &=\prod_{i=1}^{k}{\frac{1}{\sqrt{2\pi\sigma^{2}}}\exp{\left[-\frac{(x_{i}-\mu)^{2}}{2\sigma^{2}}\right]}}\\ &=\prod_{i=1}^{k}{\frac{1}{\sqrt{2\pi\sigma^{2}}}}\cdot\prod_{i=1}^{k}{\exp{\left[-\frac{(x_{i}-\mu)^{2}}{2\sigma^{2}}\right]}}\\ \\ \prod_{i=1}^{k}{\frac{1}{\sqrt{2\pi\sigma^{2}}}} &=\left(2\pi\sigma^{2}\right)^{-k/2}\\ &=(2\pi)^{-k/2}\cdot(\sigma^{2})^{-k/2}\\ \prod_{i=1}^{k}{\exp{\left[-\frac{(x_{i}-\mu)^{2}}{2\sigma^{2}}\right]}} &=\exp{\left[\sum_{i=1}^{k}{-\frac{(x_{i}-\mu)^{2}}{2\sigma^{2}}}\right]}\\ &=\exp{\left[-\frac{1}{2\sigma^{2}}\sum_{i=1}^{k}{(x_{i}-\mu)^{2}}\right]}\\ &=\exp{\left[-\frac{1}{2}\cdot\frac{\nu S^{2}}{\sigma^{2}}\right]}\\ \\ \therefore p\left(x_{1},\cdots,x_{k}\mid\sigma^{2}\right) &=(2\pi)^{-k/2}\cdot(\sigma^{2})^{-k/2}\cdot\exp{\left[-\frac{\nu}{2\sigma^{2}}\cdot S^{2}\right]}\\ &\propto\left(\sigma^{2}\right)^{-k/2}\cdot\exp{\left[-\frac{1}{2}\cdot\frac{\nu S^{2}}{\sigma^{2}}\right]} \end{aligned}\]

• posterior of $\sigma^{2}$:

  \[\begin{aligned} p\left(\sigma^{2}\mid x_{1},\cdots,x_{k}\right) &\propto p\left(x_{1},\cdots,x_{k}\mid\sigma^{2}\right)p\left(\sigma^{2}\right)\\ &\propto\left(\sigma^{2}\right)^{-k/2}\cdot\exp{\left[-\frac{1}{2}\cdot\frac{\nu S^{2}}{\sigma^{2}}\right]}\cdot\frac{1}{\sigma^{2}} \end{aligned}\]

• change of variables:

  \[\begin{gathered} z:=\frac{\nu S^{2}}{\sigma^{2}} \end{gathered}\]

• posterior of $z$:

  \[\begin{aligned} \quad p_{z}(z)\mathrm{d}z &=p_{\sigma^{2}}\left(\sigma^{2}\right)\mathrm{d}\sigma^{2}\\ \therefore p_{z}(z\mid x_{1},\cdots,x_{k}) &\propto p_{\sigma^{2}}\left(\frac{\nu S^{2}}{z}\right)\cdot\frac{\nu S^{2}}{z^{2}}\\ &\propto(\nu S^{2}/z)^{-k/2}\cdot\exp{\left[-\frac{\nu S^{2}}{2\nu S^{2}/z}\right]}\cdot\frac{1}{\nu S^{2}/z}\cdot\frac{\nu S^{2}}{z^{2}}\\ &=\left(\nu S^{2}\right)^{-k/2}\cdot z^{k/2-1}\cdot\exp{\left[-\frac{1}{2}z\right]}\\ &\approx z^{k/2-1}\cdot\exp{\left[-\frac{1}{2}z\right]}\\ &\approx \chi^{2}(k) \end{aligned}\]

• therefore, sample variance of gaussian distribution, $S^{2}$, follows a chi-square distribution.

  \[\begin{aligned} z=\frac{\nu S^{2}}{\sigma^{2}}=\sum_{i=1}^{k}{\left(\frac{x_{i}-\mu}{\sigma}\right)^{2}} \sim\chi^{2}(k) \end{aligned}\]

student’s t

---

• gaussian random variable:

  \[X_{i}\sim\mathcal{N}(\mu,\sigma^{2})\]

• standardization:

  \[Z=\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}\sim\mathcal{N}(0,1)\]

• If the population variance $\sigma^{2}$ is unknown, the sample variance $S^{2}$ can be used:

  \[S^{2}=\frac{1}{\nu}\sum_{i=1}^{n}{\left(X_{i}-\overline{X}\right)^{2}}\]

• chi-squared dist.:

  \[\begin{aligned} U\sim\chi^{2}(\nu) \end{aligned}\]

• chi-squared variable can be represented by $S^{2}$:

  \[\begin{aligned} U &=\sum_{i=1}^{n}{\left(\frac{X_{i}-\overline{X}}{\sigma}\right)^{2}}\\ &=\frac{1}{\sigma^{2}}\cdot\nu S^{2} \end{aligned}\]

• as a result, when the population variance is unknown, the test statistic can be replaced by the ratio of the chi-square random variable to the standard normal random variable:

  \[\begin{aligned} \frac{\overline{X}-\mu}{S/\sqrt{n}} &=\underbrace{\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}}_{=:Z}\cdot\frac{\sigma}{S}\\ &=Z\cdot\frac{1}{\sqrt{S^{2}/\sigma^{2}}}\\ &=\frac{Z}{\sqrt{U/\nu}}\quad\left(\because\frac{S^{2}}{\sigma^{2}}=\frac{U}{\nu}\right) \end{aligned}\]

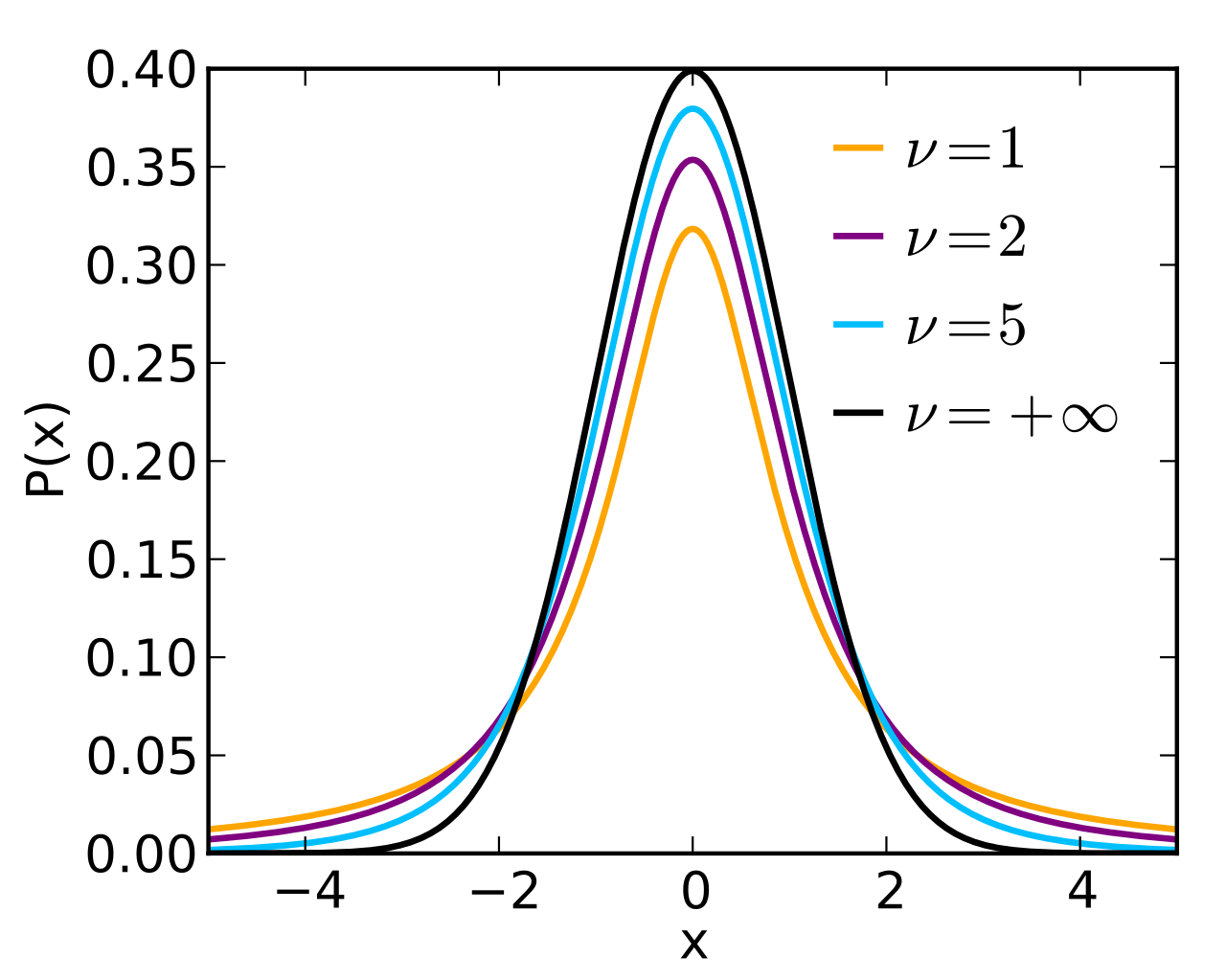
• the ratio of the chi-square random variable to the standard normal random variable is defined as the Student’s t random variable:

  \[T=\frac{Z}{\sqrt{U/\nu}}\sim t(\nu),\quad Z \perp U\]