Hierarchical Clustering

Hierarchical Clustering

---

• 정의 : 계층적 트리모형을 활용하여 개별 개체들을 유사한 개체/군집과 계층적으로 통합하거나, 표본을 유의미하게 구분되는 지점에서 계층적으로 분할해가는 알고리즘

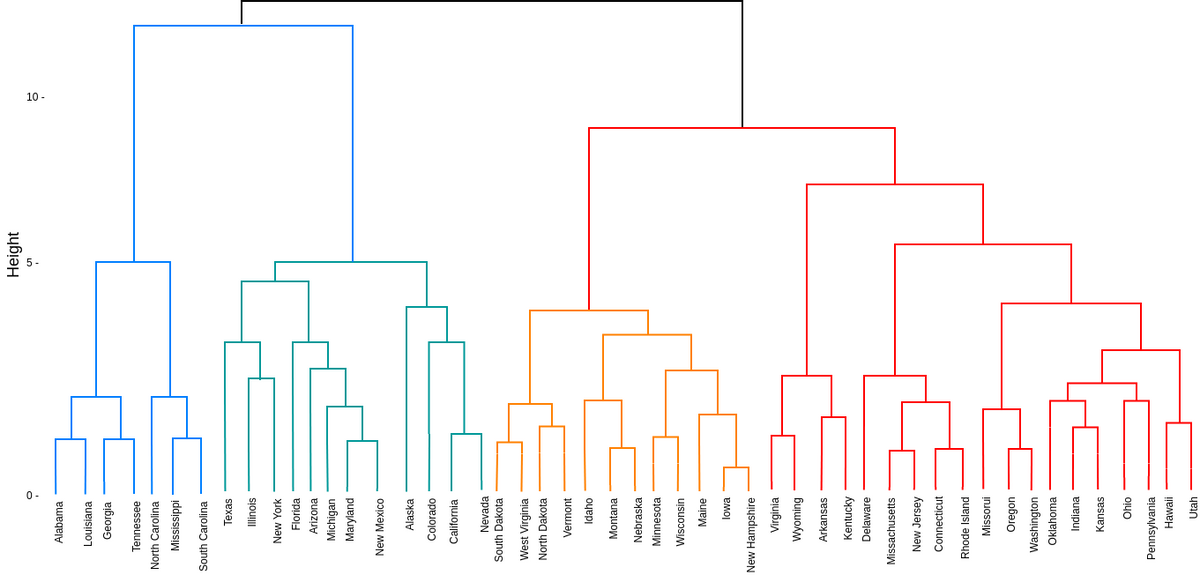
• 덴드로그램(Dendrogram) : 결합 혹은 분할하는 순서를 나타내는 계층적 트리모형

  

• 종류

  

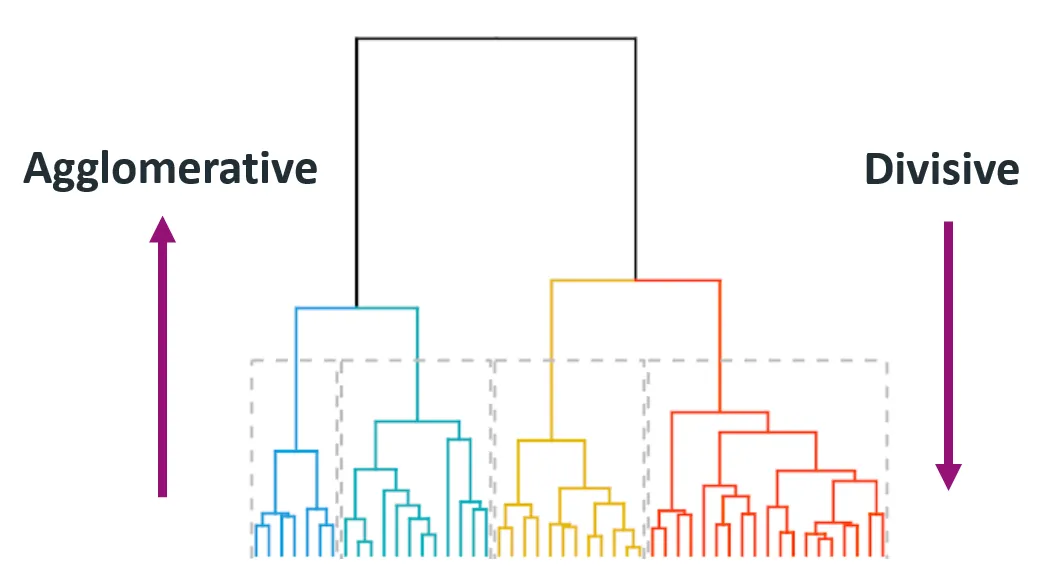
  • 상향식 군집화(Agglomerative Clustering) : 개별 개체들을 유사한 개체/군집과 계층적으로 통합해가는 방식
  • 하향식 군집화(Divisive Clustering) : 표본을 유의미하게 구분되는 지점마다 계층적으로 분할해가는 방식

How to Agglomerative Clustering

---

1. 모든 개체를 개별 군집으로서 정의함

   \[C_{i} = \{\overrightarrow{x}_{i}\} \quad \text{for} \quad i=1,2,\cdots, n\]

2. 군집 간 거리 행렬을 계산함

   \[\mathbf{D}_{i,j}=d(C_{i},C_{j})\]

3. 가장 가까운 두 개의 군집을 하나의 군집으로 통합함

   \[\begin{aligned} C_{k}&=\hat{C}_{i} \cup \hat{C}_{j}\\ \hat{C}_{i},\hat{C}_{j}&=\text{arg} \min_{C_{i},C_{j}}{d(C_{i},C_{j})} \end{aligned}\]

4. 군집 간 거리 행렬을 갱신함

   \[\mathbf{D}_{N} = \mathbf{D}_{N-1} \quad \text{Recalculate} \quad d(C_{i^{\forall} \ne k},C_{k})\]

5. 모든 개체가 하나의 군집으로 통합될 때까지 ③, ④의 과정을 반복함

How to Calculate Distance

---

• Single Linkage(Minimum Distance) : 각 군집에 속한 개체들 사이 거리 최소값

  \[\begin{aligned} d(\mathbf{A},\mathbf{B}) &= \min_{\overrightarrow{a} \in \mathbf{A},\overrightarrow{b} \in \mathbf{B}}{d(\overrightarrow{a},\overrightarrow{b})} \end{aligned}\]

• Complete Linkage(Maximum Distance) : 각 군집에 속한 개체들 사이 거리 최대값

  \[\begin{aligned} d(\mathbf{A},\mathbf{B}) &= \max_{\overrightarrow{a} \in \mathbf{A},\overrightarrow{b} \in \mathbf{B}}{d(\overrightarrow{a},\overrightarrow{b})} \end{aligned}\]

• Average Linkage(Mean Distance) : 각 군집에 속한 개체들 사이 거리 평균

  \[\begin{aligned} d(\mathbf{A},\mathbf{B}) &= \sum_{\overrightarrow{a} \in \mathbf{A}}\sum_{\overrightarrow{b} \in \mathbf{B}}{d(\overrightarrow{a},\overrightarrow{b})} \end{aligned}\]

• Centroid Linkage(Distance Between Centroids) : 각 군집 중심 간 거리

  \[\begin{aligned} d(\mathbf{A},\mathbf{B}) &= d(\overrightarrow{\mu}_{A},\overrightarrow{\mu}_{B})\\ \overrightarrow{\mu}_{A} &= \frac{1}{\vert\mathbf{A}\vert}\sum_{\overrightarrow{a} \in \mathbf{A}}{\overrightarrow{a}}\\ \overrightarrow{\mu}_{B} &= \frac{1}{\vert\mathbf{B}\vert}\sum_{\overrightarrow{b} \in \mathbf{B}}{\overrightarrow{b}} \end{aligned}\]

• Ward’s Method : 병합 후 SSE와 병합 전 개별 군집의 SSE의 합의 차

  \[\begin{aligned} d(\mathbf{A},\mathbf{B}) &= \sum_{\overrightarrow{c} \in \mathbf{C}}{d(\overrightarrow{c},\overrightarrow{\mu}_{C})} - \Big[\sum_{\overrightarrow{a} \in \mathbf{A}}{d(\overrightarrow{a},\overrightarrow{\mu}_{A})} + \sum_{\overrightarrow{b} \in \mathbf{B}}{d(\overrightarrow{b},\overrightarrow{\mu}_{B})}\Big]\\ \mathbf{C} &= \mathbf{A} \cup \mathbf{B} \end{aligned}\]

---

이미지 출처

• https://towardsdatascience.com/hierarchical-clustering-explained-e59b13846da8
• https://harshsharma1091996.medium.com/hierarchical-clustering-996745fe656b