Hypothesis Testing

Hypothesis Testing

---

• 통계적 가설(Statistical Hypothesis) : 모집단의 모수에 대한 주장
  • 귀무가설(Null-Hypothesis; $H_0$) : 사실이 아니라는 충분한 근거를 얻기 전에는 사실이라고 믿어지는 가설
  • 대립가설(Alternative Hypothesis; $H_1$) : 연구자의 주장으로서 귀무가설이 기각될 때 채택되는 가설
• 가설검정(Hypothesis Testing) : 귀무가설을 기각할 충분한 증거가 있는지 살핌으로써 대립가설을 우회로 증명하는 절차
  1. 귀무가설과 대립가설 설정
  2. 유의수준 설정
  3. 모수 추정법 적용 가능 여부 검토
  4. 검정통계량과 p-value 도출
  5. 귀무가설 기각 여부 결정
  6. 검정 결과 해석

Type

---

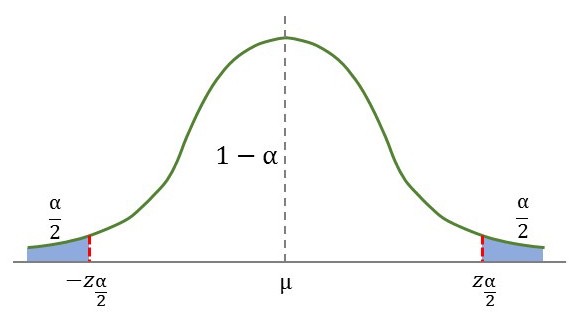
• 양측검정(Two-Sided Test) : 귀무가설에 대한 기각역을 양측에 설정하는 검정

  

  \[\begin{aligned} H_0&:\;\mu=70,\\ H_1&:\;\mu\ne70 \end{aligned}\]

• 단측검정(One-Sided Test) : 귀무가설에 대한 기각역을 단측에만 설정하는 검정

  • 우측검정 : 기각역을 우측에만 설정하는 검정

    

    \[\begin{aligned} H_0&:\;\mu \le 70,\\ H_1&:\;\mu > 70 \end{aligned}\]

  • 좌측검정 : 기각역을 좌측에만 설정하는 검정

    

    \[\begin{aligned} H_0&:\;\mu=70,\\ H_1&:\;\mu<70 \end{aligned}\]

Error

---

• 오류(Error) : 사실과 다르게 판단함

  

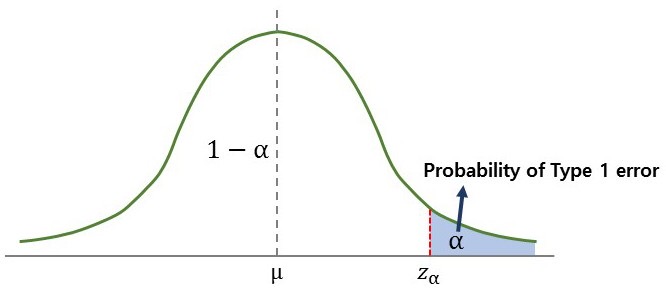
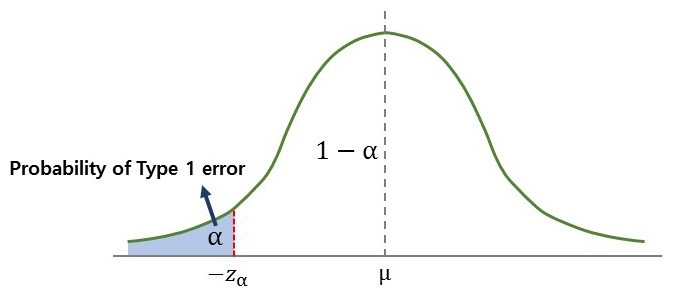
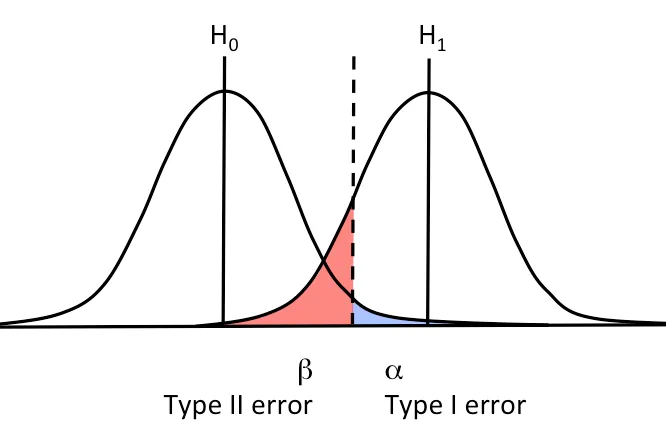
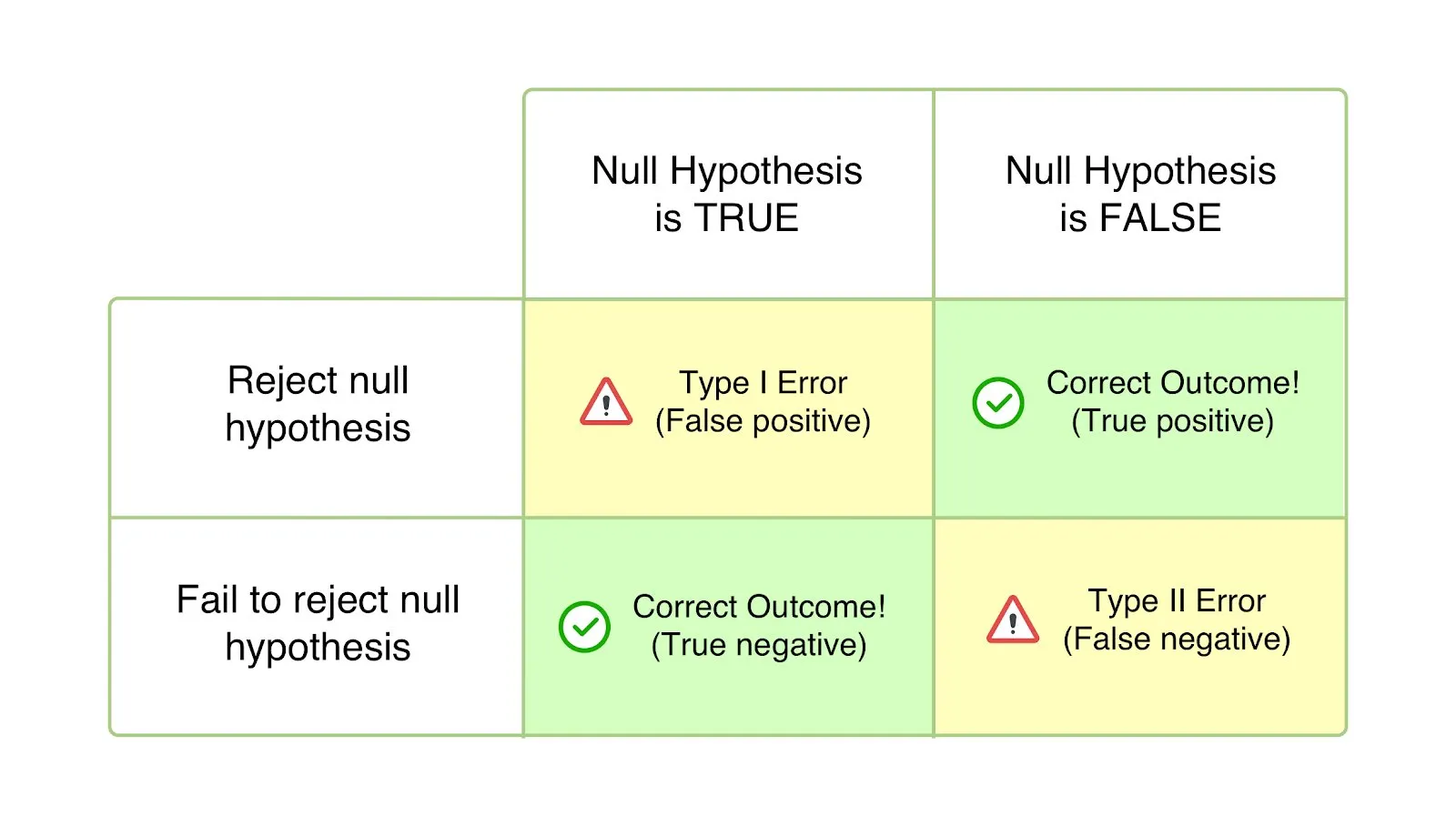
  • 제1종 오류(Type 1 Error) : 귀무가설이 참일 때 귀무가설을 기각하는 오류
  • 제1종 오류(Type 2 Error) : 귀무가설이 거짓일 때 귀무가설을 기각하지 않는 오류

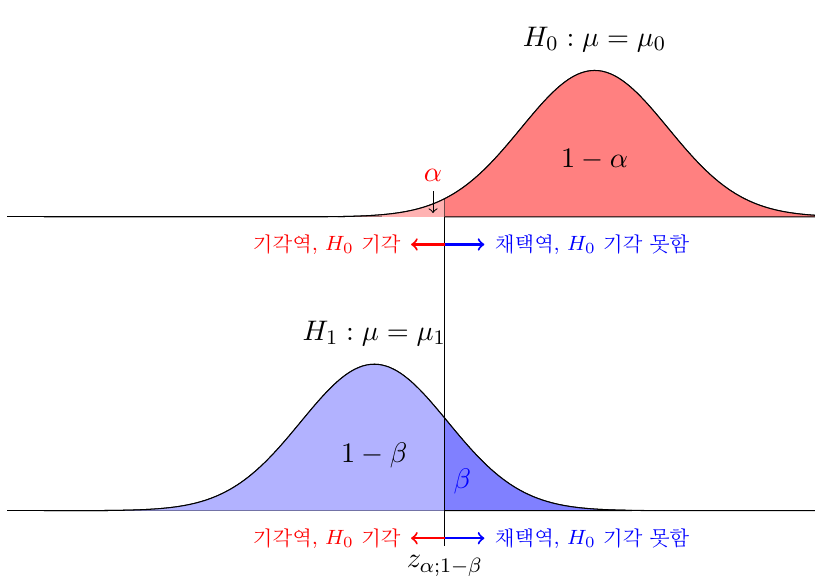
• 검정의 유의수준(Significance Level) : 제1종 오류를 범할 확률

  \[\alpha\]
  • 통계학에서는 보수적 태도(귀무가설을 기각하지 않으려는 태도)를 취하므로 제1종 오류에 민감함

• 검정의 신뢰수준(Confidence Level) : 제1종 오류를 범할 확률 $\alpha$ 에 대하여, 귀무가설이 참일 때 귀무가설을 기각하지 않을 확률

  \[1-\alpha\]

• 검정의 검정력(Power) : 제2종 오류를 범할 확률 $\beta$ 에 대하여, 귀무가설이 거짓일 때 귀무가설을 기각할 확률

  \[1-\beta\]

Test Statistic

---

• 검정통계량(Test Statistic) : 귀무가설이 참이라고 가정했을 때 얻은 결과

  

  \[\begin{aligned} Z &= \frac{\overline{X}-\mu_{0}}{\sigma / \sqrt{n}} \end{aligned}\]

• 검정통계량의 분포:

  \[\begin{aligned} Z &= \frac{\overline{X}-\mu_{0}}{\sigma / \sqrt{n}}\\ &= \frac{\overline{X}-\mu}{\sigma / \sqrt{n}} + \frac{\mu-\mu_{0}}{\sigma / \sqrt{n}}\\ &= \frac{\mu-\mu_{0}}{\sigma / \sqrt{n}} \quad (\because \mathbb{E}\left[\overline{X}\right]=\mu) \end{aligned}\]

  • 귀무가설이 참일 경우($\mu = \mu_{0}$):

    \[\begin{aligned} Z \sim \mathcal{N}(0,1) \quad (\because \frac{\mu-\mu_{0}}{\sigma / \sqrt{n}} = 0) \end{aligned}\]

  • 귀무가설이 참이 아닐 경우($\mu \ne \mu_{0}$):

    \[\begin{aligned} Z \sim \mathcal{N}(\frac{\mu-\mu_{0}}{\sigma / \sqrt{n}},1) \quad (\because \frac{\mu-\mu_{0}}{\sigma / \sqrt{n}} \ne 0) \end{aligned}\]

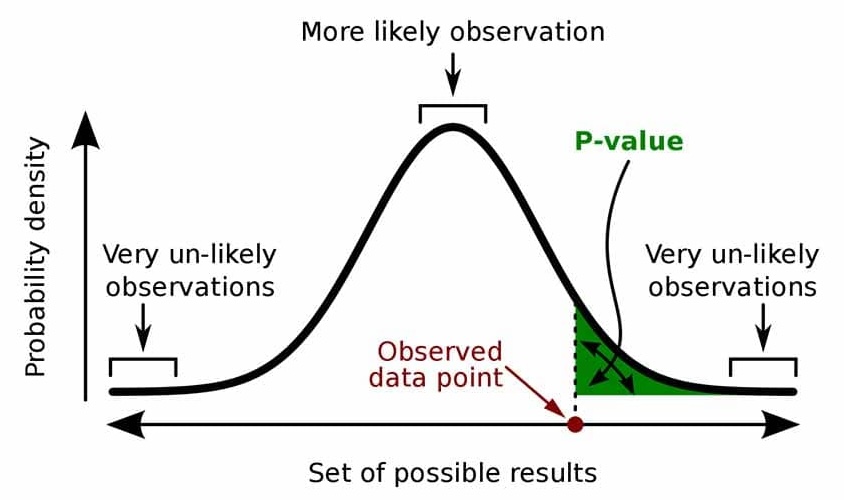
• 유의확률(Significance Probability Value) : 검정통계량($Z$)보다 극단적인 결과($Y$)가 관측될 확률로서, 표본이 귀무가설과 양립하는 정도

  

  \[\begin{aligned} \mathrm{p-value} &= P\left(\vert Y \vert \ge \vert Z \vert \mid H_{0}\right), \quad Y \sim N(0,1) \end{aligned}\]

Rejection & Interpretation

---

• 기각역(Critical Region): 귀무가설을 기각하는 영역

  \[\begin{aligned} Z \notin \mathcal{R} \end{aligned}\]

  • 기각치(Reject Value)를 활용한 기각역 설정:

    \[Z_{\alpha/2},\quad Z_{\alpha}\]
    • 양측검정: \(\mathcal{R}:=\left\{Z \mid \vert Z \vert > Z_{\alpha/2}\right\}\)
    • 우측검정: \(\mathcal{R}:=\left\{Z \mid Z > Z_{\alpha}\right\}\)
    • 좌측검정: \(\mathcal{R}:=\left\{Z \mid Z < -Z_{\alpha}\right\}\)

  • 유의수준(Significance Level)을 활용한 기각역 설정:

    \[\begin{aligned} \mathcal{R} :=\left\{Z \mid \mathrm{p-value}(Z) \ge \alpha\right\} \end{aligned}\]

• 통계적 유의성(Statistically Significant) : 실험 결과가 우연에 의한 것이 아니라 실제 현상을 반영한다고 판단할 수 있는 정도

  • Reject $H_{0}$:

    귀무가설을 $\alpha \times 100 \%$ 유의수준에서 기각하지 않는다. 즉, $\alpha \times 100 \%$ 유의수준에서 모평균 $\mu$ 는 $\mu_{0}$ 과 통계적으로 유의한 차이가 있다고 볼 수 없다. 이에 따라 귀무가설은 제한적으로 사실이라 간주될 수 있다.

  • Fail to Reject $H_{0}$:

    귀무가설을 $\alpha \times 100 \%$ 유의수준에서 기각한다. 즉, $\alpha \times 100 \%$ 유의수준에서 모평균 $\mu$ 는 $\mu_0$ 과 통계적으로 유의한 차이가 있다. 이에 따라 대립가설은 잠정적으로 사실이라 간주될 수 있다.

---

Sourse

• https://u5man.medium.com/to-err-is-human-what-the-heck-is-type-i-and-type-ii-error-b2c78190a45c
• https://wikidocs.net/163986