ID Embedding based Latent Factor Model

How to aggregate

---

• 요소별 곱(Element-wise Product): 두 벡터 간 상응하는 차원끼리 곱셈하는 방법
  • 사용자, 아이템 잠재요인 공간 동일 가정
  • 잠재요인 차원 간 독립성 가정
  • 사용자-아이템 쌍별(Pairwise) 상호작용(Interaction) 신호 반영 표현
  • 동일 차원 상호작용만 포착하므로 다차원 상호작용 반영 불가
• 벡터 결합(Vector Concatenation): 두 벡터를 결합하는 방법
  • 사용자, 아이템 잠재요인 공간 독립 가정
  • 사용자, 아이템 벡터 정보 보존 표현
  • 모형이 사용자-아이템 쌍별(Pairwise) 상호작용(Interaction) 신호 직접 학습
• 외적(Outer Product): 두 벡터 간 외적하는 방법
  • 사용자, 아이템 잠재요인 공간 동일 가정
  • 잠재요인 차원 간 종속성 가정
  • 그 대각성분은 요소별 곱셈에서 포착하는 동일 차원 간 상호작용 신호에 해당함

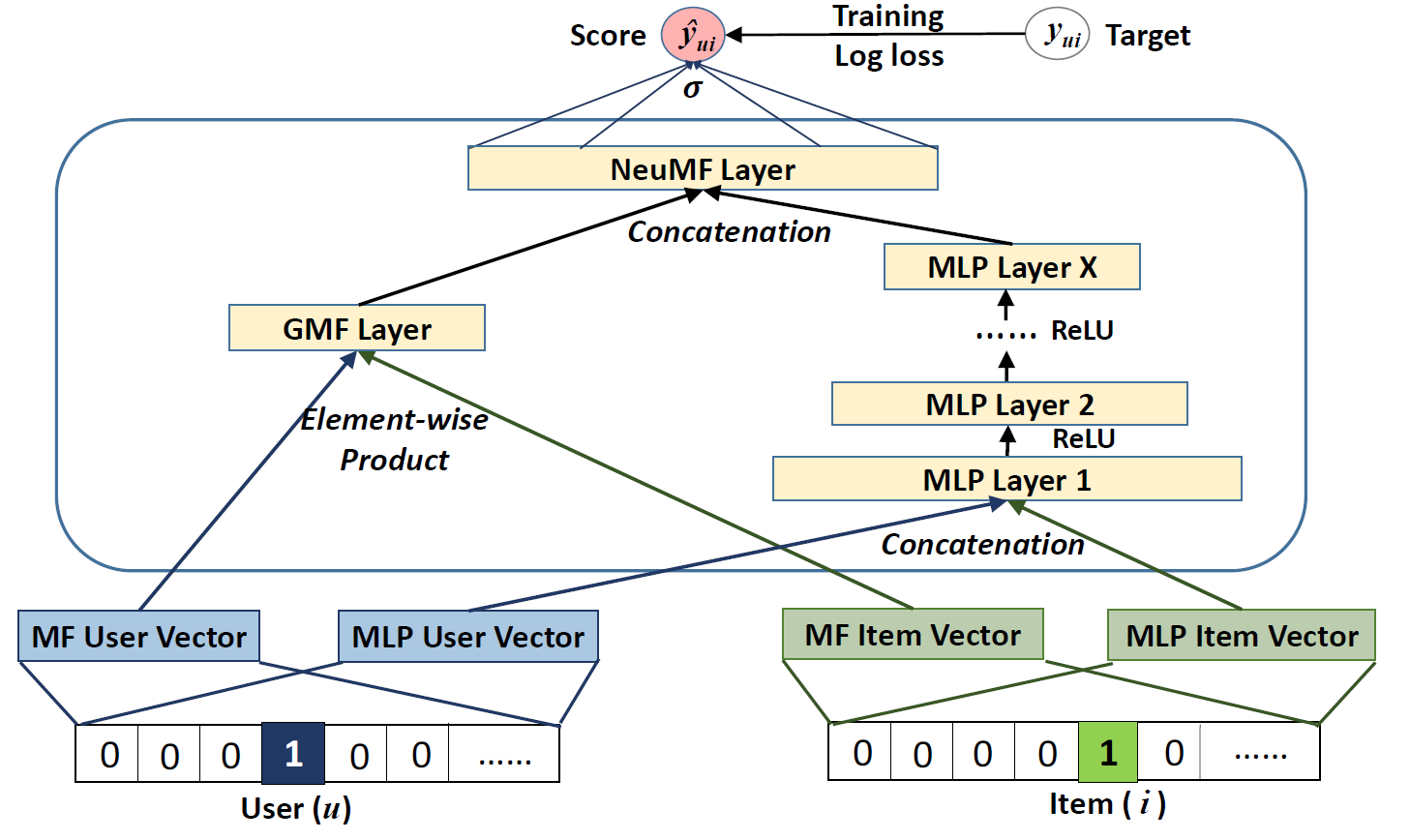
NeuMF

---

• 문제 의식: 내적(Inner Product) 기반 잠재요인 모형의 한계점
  • 내적은 사용자와 아이템 간 동일 차원 상호작용을 포착하고 이를 단순 합산하는 방법임
  • 사용자와 아이템 간 상호작용은 개별 차원에서 출력하는 신호 간에 경중이 있을 수 있음
  • 사용자와 아이템 간 상호작용은 비선형적일 수 있고, 다차원 간에도 성립할 수 있음
• NeuMF: 선형 매칭 함수 학습 모듈과 비선형 매칭 함수 학습 모듈을 병렬 학습하는 앙상블 모형
  • He, X., Liao, L., Zhang, H., Nie, L., Hu, X., & Chua, T. S.
    (2017, April).
    Neural collaborative filtering.
    In Proceedings of the 26th international conference on world wide web (pp. 173-182).
• Components
  • GMF(Generalized Matrix Factorization) : 요소별 곱 기반 선형 매칭 함수 모듈
  • NCF(Neural Collaborative Filtering) : 벡터 결합 및 다층 신경망(MLP) 기반 비선형 매칭 함수 학습 모듈
  • NeuMF(Neural Matrix Factorization) : GMF 와 NCF 의 예측 벡터(Predictive Vector)를 종합하여 예측을 수행하는 앙상블 모형

Notation

---

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\overrightarrow{\mathbf{u}}_{u} \in \mathbb{R}^{K}$: user latent factor vector
• $\overrightarrow{\mathbf{v}}_{i} \in \mathbb{R}^{K}$: item latent factor vector
• $\overrightarrow{\mathbf{z}}_{u,i} \in \mathbb{R}^{K}$: predictive vector of user $u$ and item $i$
• $\hat{y}_{u,i}$: interaction probability of user $u$ and item $i$

How to Modeling

---

• NeuMF is GMF & NCF Ensemble

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot [\overrightarrow{\mathbf{z}}_{u,i}^{\text{(GMF)}} \oplus \overrightarrow{\mathbf{z}}_{u,i}^{\text{(NCF)}}]) \end{aligned}\]

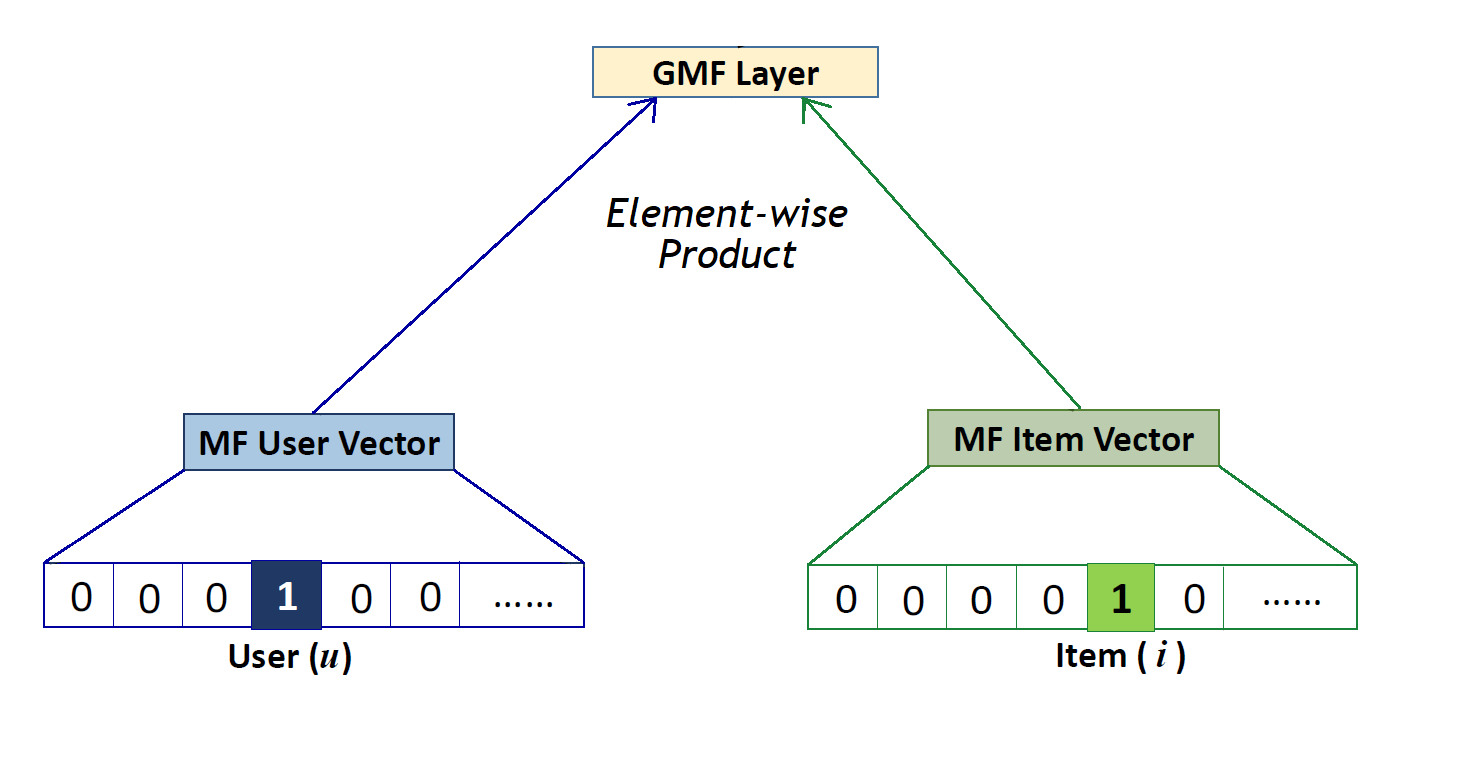
GMF

• ID Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \text{Emb}(u)\\ \overrightarrow{\mathbf{v}}_{i} &= \text{Emb}(i) \end{aligned}\]

• Predictive Vector of user $u$ and item $i$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \overrightarrow{\mathbf{u}}_{u} \odot \overrightarrow{\mathbf{v}}_{i} \end{aligned}\]

• If use GMF as a single prediction module:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot \overrightarrow{\mathbf{z}}_{u,i}) \end{aligned}\]

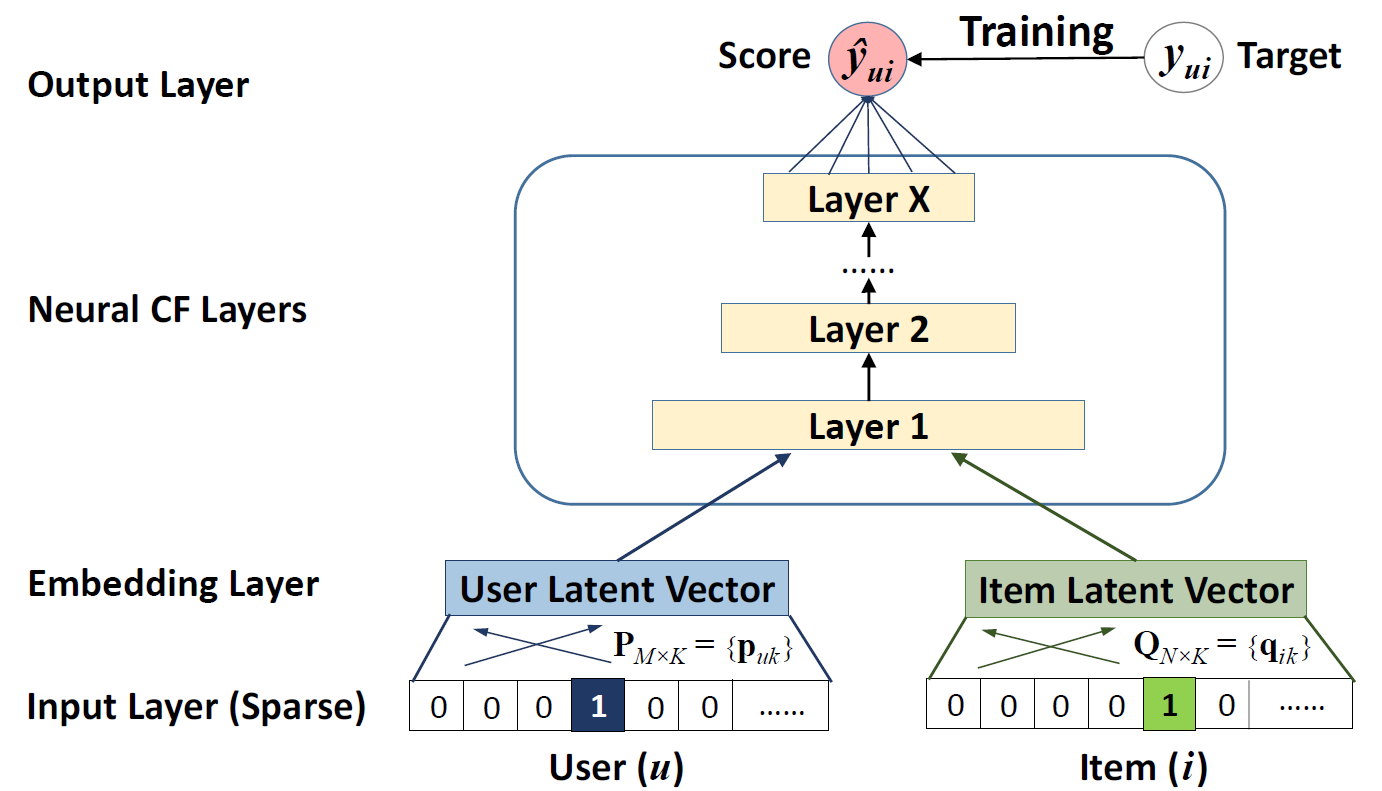
NCF

• ID Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \text{Emb}(u)\\ \overrightarrow{\mathbf{v}}_{i} &= \text{Emb}(i) \end{aligned}\]

• Predictive Vector of user $u$ and item $i$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{u}}_{u} \oplus \overrightarrow{\mathbf{v}}_{i}) \end{aligned}\]

• If use NCF as a single prediction module:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot \overrightarrow{\mathbf{z}}_{u,i}) \end{aligned}\]

---

Source

• https://iq.opengenus.org/neural-collaborative-filtering/