Integration

Integration

---

• 미분(Differentiation): $F(x)$ 를 $\Delta x$ 단위로 쪼개는 방법

  \[\begin{aligned} f(x) &= \frac{F(x + \Delta x)-F(x)}{\Delta x} \end{aligned}\]

• 적분(Integration): 미분소 $f(x) \times \Delta x$ 를 쌓는 방법

  \[\begin{aligned} F(x) &=\sum_{i}{f(x_{i}) \times \Delta x} \end{aligned}\]

• 부정적분(Indefinite Integral): 미분의 역연산으로서, 어떤 함수 $f(x)$ 를 미분계수로 취하는 모든 함수 $F(x) + C$ 를 구하는 연산

  \[\begin{aligned} F(x) + C &= \int{f(x)\mathrm{d}x}\\ &= \lim_{\Delta x \to 0}{\sum_{i}{f(x_{i}) \times \Delta x}} \end{aligned}\]
  • $F(x)$: 원시 함수
  • $f(x)$: 피적분 함수 혹은 미분계수
  • $C$: 적분 상수
• 부정적분의 연산 규칙
  • $\int{\alpha \cdot f(x)\mathrm{d}x} = \alpha \cdot \int{f(x)\mathrm{d}x}$
  • $\int{[f(x) \pm g(x)] \mathrm{d}x} = \int{f(x)\mathrm{d}x} \pm \int{g(x)\mathrm{d}x}$
  • $\int{x^{n}\mathrm{d}x} = x^{n+1}/(n+1) + C$
  • $\int{e^{x}\mathrm{d}x} = e^{x}+C$
  • $\int{1/x\mathrm{d}x} = \ln{\vert x \vert}+C$
  • $\int{f^{\prime}(x)/f(x)\mathrm{d}x} = \ln{\vert f(x) \vert}+C$

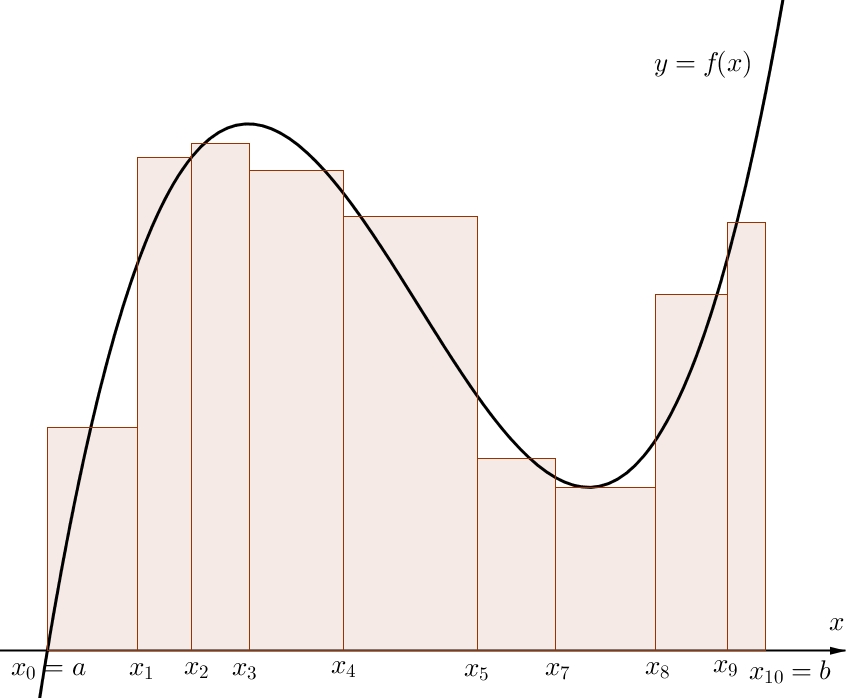
• 정적분(Definite Integral) : $x \in [a,b]$ 과 피적분함수 $f(x)$ 로 둘러싸인 면적의 너비를 구하는 연산

  \[\begin{aligned} S &= \lim_{\Delta x \to 0}{\sum_{i=a}^{b}{f(x_{i}) \times \Delta x}}\\ &= \int_{a}^{b}{f(x)\mathrm{d}x} \\ &= F(b) - F(a) \end{aligned}\]
  • $a$ : 적분의 아래 한계
  • $b$ : 적분의 위의 한계
• 정적분의 연산 규칙
  • $\mathrm{d}/\mathrm{d}x \int_{a}^{x}{f(t)\mathrm{d}t} = f(x)$
  • $\int_{a}^{b}{\alpha f(x)\mathrm{d}x} = \alpha \int_{a}^{b}{f(x)\mathrm{d}x}$
  • $\int_{a}^{b}{[f(x) \pm g(x)]\mathrm{d}x} = \int_{a}^{b}{f(x)\mathrm{d}x} \pm \int_{a}^{b}{g(x)\mathrm{d}x}$
  • $\int_{a}^{a}{\alpha f(x)\mathrm{d}x} = 0$
  • $\int_{a}^{b}{\alpha f(x)\mathrm{d}x} = -\int_{b}^{a}{\alpha f(x)\mathrm{d}x}$
  • $\int_{a}^{b}{\alpha f(x)\mathrm{d}x} + \int_{b}^{c}{\alpha f(x)\mathrm{d}x} = \int_{a}^{c}{\alpha f(x)\mathrm{d}x},\quad (a<b<c)$

Multiple Integral

---

• 중적분(Multiple Integral) : 영역 $B$ 에서 적분 가능한 다변수함수 $y=f(x_{1},x_{2},\cdots,x_{N})$ 에 대하여 변수 $x_{1},x_{2},\cdots,x_{N}$ 에 대한 정적분

  \[\begin{aligned} \int_{x_{N}} \cdots \int_{x_2} \int_{x_1} f(x_{1},x_{2},\cdots,x_{n}) \mathrm{d}x_{1} \mathrm{d}x_{2} \cdots \mathrm{d}x_{N} \end{aligned}\]

• 영역 $B$ 를 다음과 같이 정의하자

  \[\begin{aligned} B &= [a,b]\times[c,d]\\ &= \{(x,y) \mid a \leq x \leq b, c \leq y \leq d\} \end{aligned}\]

• 2변수함수 $z=f(x,y)$ 는 영역 $B$ 에서 적분 가능한 함수임

  \[\begin{aligned} \lim_{x \to k-0}{f(x,y)}=\lim_{x \to k+0}{f(x,y)}=f(k,y) \quad (a \leq k \leq b)\\ \lim_{y \to k-0}{f(x,y)}=\lim_{y \to k+0}{f(x,y)}=f(x,k)\quad(c \leq k \leq d)\\ \end{aligned}\]

• 피적분함수 $z=f(x,y)$ 를 영역 $B$ 에서 $y$ 에 대하여 적분하면:

  \[\begin{aligned} g(x) &= \int_{c}^{d}{z\mathrm{d}y}\\ &= \int_{c}^{d}{f(x,y)\mathrm{d}y}\\ &= F(x,d)-F(x,c) \end{aligned}\]

• $x$ 에 관한 함수 $g(x)$ 를 영역 $B$ 에서 $x$ 에 대하여 적분하면:

  \[\begin{aligned} \int_{a}^{b}{g(x)\mathrm{d}x} &= G(b) - G(a) \end{aligned}\]

• 이상을 요약하면 다음과 같음

  \[\begin{aligned} \int_{a}^{b}\left(\int_{c}^{d}{z}\mathrm{d}y\right)\mathrm{d}x &= \int_{a}^{b}\int_{c}^{d}{f(x,y)}\mathrm{d}y\mathrm{d}x \end{aligned}\]

Integration by Parts

---

• 부분적분(Integration by Parts): 곱의 적분법

  \[\begin{aligned} \int{u(x)v^{\prime}(x)\mathrm{d}x} &= u(x)v(x) - \int{u^{\prime}(x)v(x)\mathrm{d}x} \end{aligned}\]
  • $\int{u^{\prime}(x)\mathrm{d}x}=\mathrm{d}u$
  • $\int{v^{\prime}(x)\mathrm{d}x}=\mathrm{d}v$

• $x$ 에 대하여 미분 가능한 함수 $u(x),v(x)$ 의 곱을 $x$ 에 대하여 미분하면:

  \[\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x}uv &= u\frac{\mathrm{d}v}{\mathrm{d}x} + v\frac{\mathrm{d}u}{\mathrm{d}x} \end{aligned}\]

• 양변에 $\mathrm{d}x$ 를 곱하면:

  \[\begin{aligned} \mathrm{\mathrm{d}}(uv) &= u \cdot \mathrm{d}v + v \cdot \mathrm{d}u \end{aligned}\]

• 양변의 일부 항목을 이항하면:

  \[\begin{aligned} u \cdot \mathrm{d}v &= \mathrm{d}(uv) - v \cdot \mathrm{d}u \end{aligned}\]

• 양변을 적분하면:

  \[\begin{aligned} \int{u \cdot \mathrm{d}v} &= uv - \int{v \cdot \mathrm{d}u} \end{aligned}\]

Integration of Rational Functions

---

• 유리함수의 적분법(integration of rational functions): $x$ 에 대하여 적분 가능한 두 함수 $f(x),g(x)$ 로 구성된 피적분함수 $f(x)/g(x)$ 의 적분법

  \[\begin{aligned} \int{\frac{f(x)}{g(x)}\mathrm{d}x} \end{aligned}\]

• $f(x),g(x)$ 를 다음과 같이 가정하자

  \[\begin{aligned} f(x) &= x^{3}-x^{2}-2\\ g(x) &= x^{2}-x \end{aligned}\]

• $f(x)$ 를 $g(x)$ 로 나누면:

  \[\begin{aligned} f(x) \div g(x) &= \frac{x^{3}-x^{2}-2}{x^{2}-x}\\ &= \frac{x^{2}(x-1)-2}{x(x-1)}\\ &= x - \frac{2}{x(x-1)} \end{aligned}\]

• 나머지를 부분분수분해하면:

  \[\begin{aligned} \frac{2}{x(x-1)} &= 2 \times \frac{1}{(x-1)-x}\left(\frac{1}{x}-\frac{1}{x-1}\right)\\ &= -\frac{2}{x} + \frac{2}{x-1} \end{aligned}\]

• $f(x)/g(x)$ 를 재정의하면:

  \[\begin{aligned} \frac{f(x)}{g(x)} &= x + \frac{2}{x} - \frac{2}{x-1} \end{aligned}\]

• 양변을 적분하면:

  \[\begin{aligned} \int{\frac{f(x)}{g(x)}\mathrm{d}x} &= \int{\left[x + \frac{2}{x} - \frac{2}{x-1}\right]\mathrm{d}x}\\ &= \int{x\mathrm{d}x} + \int{\frac{2}{x}\mathrm{d}x} - \int{\frac{2}{x-1}\mathrm{d}x} \end{aligned}\]

Improper Integral

---

• 이상적분(Improper Integral): 극한치의 적어도 한 개가 무한일 경우의 적분법

  \[\begin{aligned} \int_{a}^{\infty}{f(x)\mathrm{d}x},\quad \int_{\infty}^{b}{f(x)\mathrm{d}x} \end{aligned}\]

• 피적분함수 $f(x)=1/x^{2}$ 에 대한 정적분:

  \[\begin{aligned} \int_{1}^{\infty}{\frac{1}{x^2}\mathrm{d}x} \end{aligned}\]

• 적분의 위의 한계 $\infty$ 를 상수 $k$ 로 치환하면:

  \[\begin{aligned} \int_{1}^{\infty}{\frac{1}{x^2}\mathrm{d}x} &= \lim_{k\to\infty}{\int_{1}^{k}{\frac{1}{x^2}\mathrm{d}x}} \end{aligned}\]

• $f(x)$ 를 $[1,k]$ 에서 정적분하면:

  \[\begin{aligned} \int_{1}^{k}{\frac{1}{x^2}\mathrm{d}x} &= \left[-\frac{1}{x}\right]^{x=k}_{x=1}\\ &= -\frac{1}{k}+1 \end{aligned}\]

• $k \to \infty$ 일 때 위 식의 값은 다음과 같음

  \[\begin{aligned} \lim_{k\to\infty}{\left[-\frac{1}{k}+1\right]} &= 1 \end{aligned}\]