Linear Discriminant Analysis

Prerequisite

---

Projection

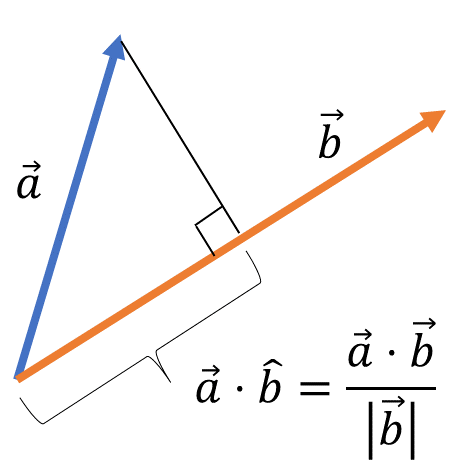
• 벡터 $\overrightarrow{a}$ 를 벡터 $\overrightarrow{b}$ 에 정사영했을 때, 정사영 벡터 $\text{proj}_{\overrightarrow{b}}(\overrightarrow{a})$ 는 다음과 같음

  \[\begin{aligned} \cos{90^{\circ}} &= \frac{(\overrightarrow{a}-p\overrightarrow{b})^{T}\overrightarrow{b}}{\Vert \overrightarrow{a}\Vert \cdot \Vert\overrightarrow{b}\Vert}\\ &= 0\\ \therefore \text{proj}_{\overrightarrow{b}}(\overrightarrow{a}) &= p\overrightarrow{b}\\ &= \left(\frac{\overrightarrow{a}^{T}\overrightarrow{b}}{\Vert\overrightarrow{b}\Vert^{2}}\right)\overrightarrow{b} \end{aligned}\]
  • $p=\displaystyle\frac{\overrightarrow{a}^{T}\overrightarrow{b}}{\Vert\overrightarrow{b}\Vert^{2}}$ : 정사영 벡터의 크기
  • $\overrightarrow{b}$ : 정사영 벡터의 방향

Covariance Matrix

• 공분산(Covariance) : 두 확률변수의 선형관계를 나타내는 지표로서, 두 확률변수의 편차(관측치와 평균 사이 거리)를 곱한 값의 평균

  \[\sigma_{XY} = \frac{1}{N}\sum_{i=1}^{N}(X_{i}-\mu_X)(Y_{i}-\mu_Y)\]

• 공분산행렬(Covariance Matrix) : $n$ 개 변수들 간 공분산을 나열한 $n \times n$ 정방행렬

  \[\Sigma= \begin{matrix} & \overrightarrow{A} & \overrightarrow{B} & \overrightarrow{C} \\ \overrightarrow{A} & \sigma_{A}^2 & \sigma_{AB} & \sigma_{AC} \\ \overrightarrow{B} & \sigma_{BA} & \sigma_{B}^2 & \sigma_{BC} \\ \overrightarrow{C} & \sigma_{CA} & \sigma_{CB} & \sigma_{C}^2 \end{matrix}\]

Linear Transformation

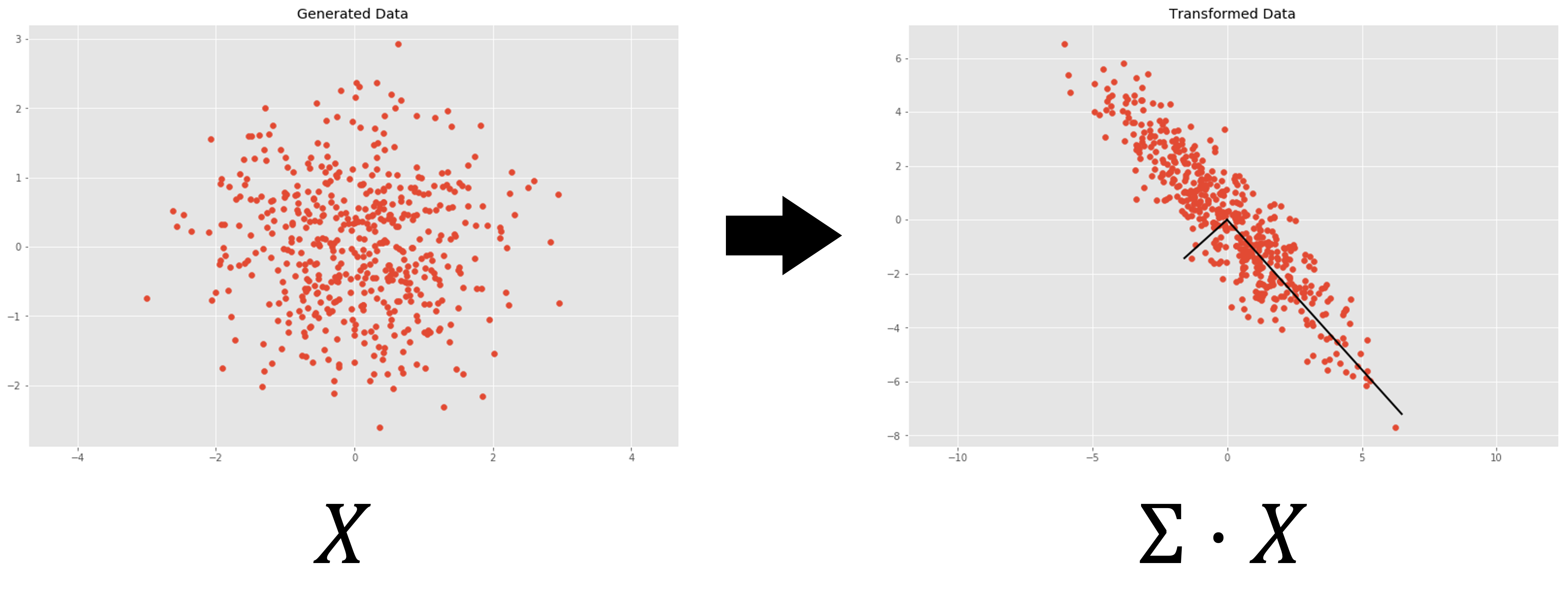
• 행렬 $\mathbf{X}$ 을 통한 선형변환은 어떤 좌표를 \(\begin{pmatrix}1\\0\end{pmatrix},\begin{pmatrix}0\\1\end{pmatrix}\) 를 기저로 사용하는 2차원 좌표계에서 \(\overrightarrow{x}_{1},\overrightarrow{x}_{2}\) 를 기저로 사용하는 2차원 좌표계로 변환하는 것을 의미함

  \[\begin{aligned} \mathbf{X} &= \begin{pmatrix} 1&3\\-2&0 \end{pmatrix}\\ &= \begin{pmatrix} \overrightarrow{x}_{1}&\overrightarrow{x}_{2} \end{pmatrix} \end{aligned}\]

• 벡터 $\overrightarrow{v}$ 는 \(\begin{pmatrix}1\\0\end{pmatrix},\begin{pmatrix}0\\1\end{pmatrix}\) 를 기저로 사용하는 2차원 좌표계의 좌표 $(-1,2)$ 를 나타냄

  \[\begin{aligned} \overrightarrow{v} &= \begin{pmatrix} 1\\-2 \end{pmatrix}\\ &= -1\begin{pmatrix}1\\0\end{pmatrix} + 2\begin{pmatrix}0\\1\end{pmatrix}\\ \end{aligned}\]

• $\mathbf{X}$ 를 통한 선형 변환 결과 \(\overrightarrow{v}\) 는 \(\overrightarrow{x}_{1},\overrightarrow{x}_{2}\) 를 기저로 사용하는 2차원 좌표계의 좌표 $(-1,2)$ 로 변환되었음

  \[\begin{aligned} \mathbf{X}\cdot\overrightarrow{v} &= \begin{pmatrix} 1&3\\-2&0 \end{pmatrix} \cdot \begin{pmatrix} 1\\-2 \end{pmatrix}\\ &= \begin{pmatrix}-5\\2\end{pmatrix}\\ &= -1\overrightarrow{x}_{1} + 2\overrightarrow{x}_{2} \end{aligned}\]

Eigen-Vector

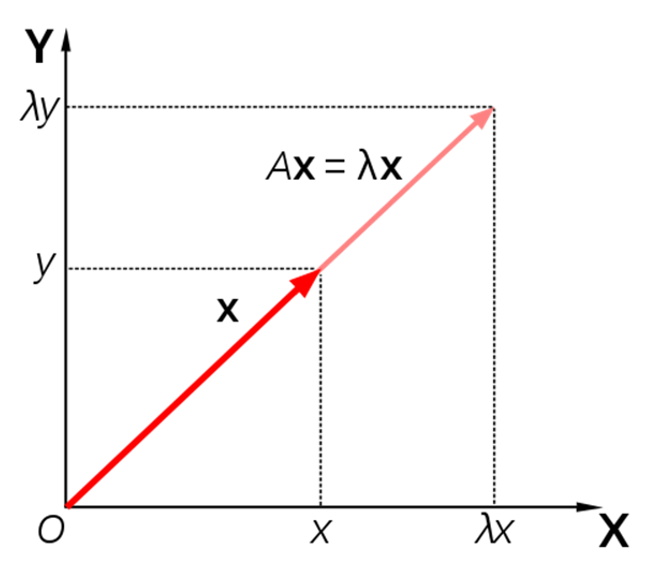
• 고유벡터(Eigen-Vector; $\overrightarrow{v}$) : 정방행렬 $A_n$ 으로 선형변환했을 때, 그 방향은 변하지 않고 단지 크기만 변하는 $\overrightarrow{0}$ 이 아닌 벡터

  \[\begin{aligned} \begin{pmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{1n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn} \end{pmatrix} \begin{pmatrix} v_{1} \\ v_{2} \\ \vdots \\ v_{n} \end{pmatrix} = \lambda \begin{pmatrix} v_{1} \\ v_{2} \\ \vdots \\ v_{n} \end{pmatrix} \Leftrightarrow A_{n \times n} \overrightarrow{v} = \lambda \overrightarrow{v} \end{aligned}\]

• 고유값(Eigen-Value; $\lambda$) : 고유벡터의 선형변환 전 크기 대비 선형변환 후 크기의 비율

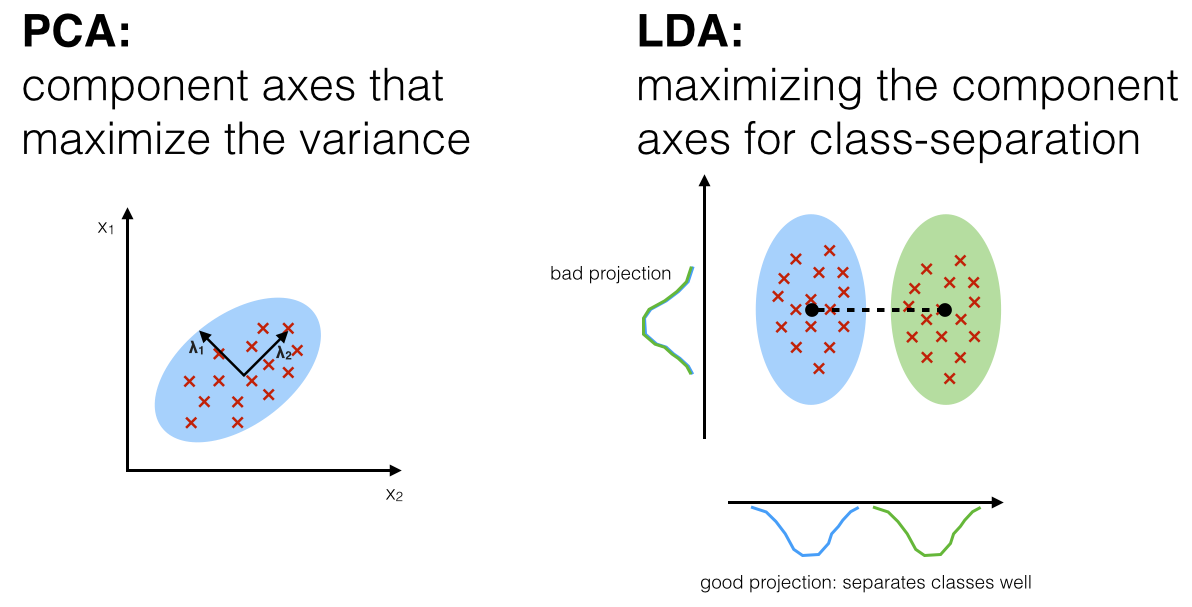
Linear Discriminant Analysis

---

• 선형 판별 분석(Linear Discriminant Analysis; LDA) : 고차원 데이터에 대하여, 주어진 클래스를 가장 잘 구분할 수 있는 새로운 저차원 직교 좌표(선형 판별 함수)를 찾는 기법

  

• 방법 : 클래스 간 분산은 최대화하는 동시에 클래스 내 관측치 간 분산은 최소화하는 성분들을 추출함

  \[\hat{\overrightarrow{w}} =\text{arg} \max_{\overrightarrow{w}}{\frac{\Sigma^{2}}{\sigma_{1}^{2}+\sigma_{2}^{2}}} \quad \text{s.t.} \quad \overrightarrow{w}^{T}\overrightarrow{w}=1\]
  • $\Sigma^{2}$ : 정사영 후 클래스 간 분산
  • $\sigma_{i}^{2}$ : 정사영 후 $i$ 번째 클래스 내 관측치 간 분산

How to Extract

---

• 정사영 후 범주 간 분산 $\Sigma^{2}$

  \[\begin{aligned} \Sigma^{2} &= (\overrightarrow{\mu}_{1}-\overrightarrow{\mu}_{2})(\overrightarrow{\mu}_{1}-\overrightarrow{\mu}_{2})^{T}\\ &= (\overrightarrow{w}^{T}\overrightarrow{m}_{1}-\overrightarrow{w}^{T}\overrightarrow{m}_{2})(\overrightarrow{w}^{T}\overrightarrow{m}_{1}-\overrightarrow{w}^{T}\overrightarrow{m}_{2})^{T}\quad(\because \overrightarrow{\mu}_{i}=\overrightarrow{w}^{T}\overrightarrow{m}_{i})\\ &= \overrightarrow{w}^{T}(\overrightarrow{m}_{1}-\overrightarrow{m}_{2})(\overrightarrow{m}_{1}-\overrightarrow{m}_{2})^{T}\overrightarrow{w}\\ &= \overrightarrow{w}^{T}\mathbf{S}_{B}\overrightarrow{w} \end{aligned}\]
  • \(\overrightarrow{m}_{i}\) : \(i\) 번째 범주 \(C_{i}\) 의 중심점 벡터
  • \(\overrightarrow{\mu}_{i}=\text{proj}_{\overrightarrow{w}}(\overrightarrow{m}_{i})\) : \(\overrightarrow{m}_{i}\) 의 정사영 벡터
  • \(\mathbf{S}_{B}\) : 범주 \(C_{i},C_{j}\) 간 편차
  • \(\Sigma\) : 정사영 후 범주 \(C_{i},C_{j}\) 간 편차

• 정사영 후 범주 내 분산 $\sigma_{i}^{2}$

  \[\begin{aligned} \sigma_{i}^{2} &= \sum_{j=1}^{ \vert C_{i} \vert }{(\overrightarrow{y}_{j}-\overrightarrow{\mu}_{i})(\overrightarrow{y}_{j}-\overrightarrow{\mu}_{i})^{T}}\quad(\overrightarrow{x}_{j} \in C_{i})\\ &= \sum_{j=1}^{ \vert C_{i} \vert }{(\overrightarrow{w}^{T}\overrightarrow{x}_{j}-\overrightarrow{w}^{T}\overrightarrow{m}_{i})(\overrightarrow{w}^{T}\overrightarrow{x}_{j}-\overrightarrow{w}^{T}\overrightarrow{m}_{i})^{T}}\quad(\because \overrightarrow{y}_{j}=\overrightarrow{w}^{T}\overrightarrow{x}_{j})\\ &= \overrightarrow{w}^{T}\left[\sum_{j=1}^{ \vert C_{i} \vert }{(\overrightarrow{x}_{j}-\overrightarrow{m}_{i})(\overrightarrow{x}_{j}-\overrightarrow{m}_{i})^{T}}\right]\overrightarrow{w}\\ &= \overrightarrow{w}^{T}\mathbf{S}_{i}\overrightarrow{w} \end{aligned}\]
  • \(\overrightarrow{x}_{j} \in C_{i}\) : \(i\) 번째 범주 \(C_{i}\) 의 \(j\) 번째 관측치 벡터
  • \(\overrightarrow{y}_{j}=\text{proj}_{\overrightarrow{w}}(\overrightarrow{x}_{j})\) : \(\overrightarrow{x}_{j}\) 의 정사영 벡터
  • \(S_{i}\) : \(i\) 번째 범주 \(C_{i}\) 의 범주 내 관측치 간 편차
  • \(\sigma_{i}\) : 정사영 후 \(i\) 번째 범주 \(C_{i}\) 의 범주 내 관측치 간 편차

• 목적 함수 재정의

  \[\begin{aligned} \hat{\overrightarrow{w}} =\text{arg} \max_{\overrightarrow{w}}{\frac{\overrightarrow{w}^{T}\mathbf{S}_{B}\overrightarrow{w}}{\overrightarrow{w}^{T}(\mathbf{S}_{1}+\mathbf{S}_{2})\overrightarrow{w}}} \quad \text{s.t.} \quad \overrightarrow{w}^{T}\overrightarrow{w}=1 \end{aligned}\]

• 라그랑주 승수법을 통한 최적화 문제 풀이

  \[\begin{aligned} L(\overrightarrow{w},\lambda) &= \frac{\overrightarrow{w}^{T}\mathbf{S}_{B}\overrightarrow{w}}{\overrightarrow{w}^{T}(\mathbf{S}_{1}+\mathbf{S}_{2})\overrightarrow{w}}-\lambda(\overrightarrow{w}^{T}\overrightarrow{w}-1)\\ \frac{\partial L(\overrightarrow{w},\lambda)}{\partial \overrightarrow{w}} &= 0\\ \therefore \left[\mathbf{S}_{B}^{-1}(\mathbf{S}_{1}+\mathbf{S}_{2})-\lambda\mathbf{I}\right]\hat{\overrightarrow{w}} &=0 \end{aligned}\]