Latent Factor Model with Attention Mechanism

DACR: History Embedding with ATTN

---

• 문제 의식: Implicit Feedback Problem
  • DeepCF
    • 표현 학습(Representation Learning): 사용자와 아이템 간 선형 관계를 바탕으로 저차원 잠재요인 공간을 효율적으로 구성
    • 매칭 함수 학습(Matching Function Learning): 다양한 매칭 함수를 근사하여 사용자와 아이템 간 비선형 상호작용 포착
  • Implicit Feedback Problem
    • 관측치의 불완전성(Observation Incompleteness): 관측과 미관측이 반드시 선호와 비선호를 의미하지 않음
    • 선호의 비가시성(Hidden Signal): 관측치의 불완전성으로 인하여 선호의 정도나 의도를 포착하기 어려움
    • 즉, 암시적 피드백 데이터는 행동 매칭 데이터이기에 선호 매칭에 사용하기 위해서는 내재된 선호 정보를 부각하고 잡음을 여과하는 절차가 필요함
• DACR(Deep Collaborative Recommendation Algorithm Based on Attention Mechanism): 사용자, 아이템 표현 및 그 결합 표현에 어텐션 메커니즘(Attention Mechanism)을 적용하여 차원별 가중치를 명시적으로 설계함으로써 입력 중 집중할(Focus) 정보를 선별하여 강조하는 앙상블 모형
  • Cui, C., Qin, J., & Ren, Q.
    (2022).
    Deep collaborative recommendation algorithm based on attention mechanism.
    Applied Sciences, 12(20), 10594.
• Components
  • ARL: Attention Representation Learning
  • AML: Attnetion Matching Function Learning
  • DACR: ARL & AML Emsemble

Notation

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\mathbf{Y} \in \mathbb{R}^{M \times N}$: user-item interaction matrix
• $\overrightarrow{\mathbf{u}}_{u} \in \mathbb{R}^{K}$: user latent factor vector
• $\overrightarrow{\mathbf{v}}_{i} \in \mathbb{R}^{K}$: item latent factor vector
• $\overrightarrow{\mathbf{z}}_{u,i}$: predictive vector of user $u$ and item $i$
• $\hat{y}_{u,i}$: interaction probability of user $u$ and item $i$
• $\delta$: softmax function
• $\sigma$: sigmoid function

How to Modeling

• DACR is ARL & AML Emsemble

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot [\overrightarrow{\mathbf{z}}_{u,i}^{\text{(ARL)}} \oplus \overrightarrow{\mathbf{z}}_{u,i}^{\text{(AML)}}]) \end{aligned}\]

ARL

• Linear Transformation:

  \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u} &= \mathbf{W} \cdot \mathbf{Y}_{u*}\\ \overrightarrow{\mathbf{q}}_{i} &= \mathbf{W} \cdot \mathbf{Y}_{*i} \end{aligned}\]
  • $\overrightarrow{\mathbf{p}}_{u} \in \mathbb{R}^{D}$
  • $\overrightarrow{\mathbf{q}}_{i} \in \mathbb{R}^{D}$

• Attention Weight:

  \[\begin{aligned} \alpha_{u} &= \delta(\mathbf{W} \cdot \overrightarrow{\mathbf{p}}_{u} + \overrightarrow{\mathbf{b}})\\ \alpha_{i} &= \delta(\mathbf{W} \cdot \overrightarrow{\mathbf{q}}_{i} + \overrightarrow{\mathbf{b}}) \end{aligned}\]

• Representation Learning:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \text{MLP}_{\text{ReLU}}\left(\overrightarrow{\mathbf{p}}_{u} \oplus [\alpha_{u} \odot \overrightarrow{\mathbf{p}}_{u}]\right)\\ \overrightarrow{\mathbf{v}}_{i} &= \text{MLP}_{\text{ReLU}}\left(\overrightarrow{\mathbf{q}}_{i} \oplus [\alpha_{i} \odot \overrightarrow{\mathbf{q}}_{i}]\right) \end{aligned}\]

• predictive vector of user $u$ and item $i$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \overrightarrow{\mathbf{u}}_{u} \odot \overrightarrow{\mathbf{v}}_{i} \end{aligned}\]

• if use ARL as a single prediction module:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot \overrightarrow{\mathbf{z}}_{u,i}) \end{aligned}\]

AML

• History Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \mathbf{W} \cdot \mathbf{Y}_{u*}\\ \overrightarrow{\mathbf{v}}_{i} &= \mathbf{W} \cdot \mathbf{Y}_{*i} \end{aligned}\]

• Vector Concatenation:

  \[\begin{aligned} \overrightarrow{\mathbf{x}}_{u,i} &= \overrightarrow{\mathbf{p}}_{u} \oplus \overrightarrow{\mathbf{q}}_{i} \end{aligned}\]

• Attention Weight:

  \[\begin{aligned} \alpha_{u,i} &= \delta(\mathbf{W} \cdot \overrightarrow{\mathbf{x}}_{u,i} + \overrightarrow{\mathbf{b}}) \end{aligned}\]

• Matching Function Learning:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \text{MLP}_{\text{ReLU}}\left(\overrightarrow{\mathbf{x}}_{u,i} \oplus [\alpha_{u,i} \odot \overrightarrow{\mathbf{x}}_{u,i}]\right) \end{aligned}\]

• if use AML as a single prediction module:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot \overrightarrow{\mathbf{z}}_{u,i}) \end{aligned}\]

DRNet: Aggregate User’s Histories

---

• 문제 의식
  • 기존 협업 필터링이 모델링하는 관계 유형
    • 잠재요인 모형(Latent Factor Model): 사용자-아이템 관계 모델링, 개인화 추천 성능 우수 (ex. NCF)
    • 아이템 기반 협업 필터링(User Free Model): 아이템-아이템 관계 모델링, 데이터 희소성 강건 (ex. SLIM, FISM)
  • 어텐션 기반 히스토리 아이템 집계 방식 (ex. NAIS)
    • 사용자가 과거에 더 선호한 아이템일수록 새로운 아이템 선택에 더 큰 영향력을 행사함
    • 사용자의 선호 정도에 기반하여 집중도를 차등 부여하여 집계할 필요가 있음
• DRNet(Dual Relation Net-work) : 사용자-아이템 매칭 함수와 아이템-아이템 매칭 함수를 병렬 학습하는 모형
  • Ji, D., Xiang, Z., & Li, Y.
    (2020).
    Dual relations network for collaborative filtering.
    IEEE Access, 8, 109747-109757.
• Components
  • Affection Network: Modeling User-Item Relation
  • Association Network: Modeling Item-Item Relation
  • Dual-Relation Network: Affection Network & Association Network Combination

Notation

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\mathbf{Y} \in \mathbb{R}^{M \times N}$: user-item interaction matrix
• $\overrightarrow{\mathbf{u}}_{u} \in \mathbb{R}^{K}$: user id embedding vector @ affection network
• $\overrightarrow{\mathbf{v}}_{i} \in \mathbb{R}^{K}$: item id embedding vector @ affection network
• $\overrightarrow{\mathbf{p}}_{i} \in \mathbb{R}^{K}$: target item id embedding vector @ association network
• $\overrightarrow{\mathbf{q}}_{j} \in \mathbb{R}^{K}$: history item id embedding vector @ association network
• $\overrightarrow{\mathbf{z}}_{u,i}$: predictive vector of user $u$ and item $i$
• $\hat{y}_{u,i}$: interaction probability of user $u$ and item $i$

How to Modeling

• Dual-Relation Network:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma\left(\overrightarrow{\mathbf{w}} \cdot [\overrightarrow{\mathbf{z}}_{u,i}^{\text{(AFFECT)}} \oplus \overrightarrow{\mathbf{z}}_{u,i}^{\text{(ASSO)}}]\right) \end{aligned}\]

Affection Network

• ID Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \text{Emb}(u)\\ \overrightarrow{\mathbf{v}}_{i} &= \text{Emb}(i) \end{aligned}\]

• Predictive Vector of user $u$ and item $i$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{u}}_{u} \odot \overrightarrow{\mathbf{v}}_{i}) \end{aligned}\]

Association Network

• ID Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{p}}_{i} &= \text{Emb}(i)\\ \overrightarrow{\mathbf{q}}_{j} &= \text{Emb}(j) \end{aligned}\]

• Global Item Vector of User $u$:

  \[\begin{aligned} \overrightarrow{\mathbf{x}}_{u} &= \text{ATTN}(\overrightarrow{\mathbf{h}},\text{Affection}(u,\forall j \in \mathcal{R}_{u}^{+} \setminus \{i\}), \mathbf{Q}[\forall j \in \mathcal{R}_{u}^{+} \setminus \{i\},:]) \end{aligned}\]

• Predictive Vector of user $u$ and item $i$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{x}}_{u} \odot \overrightarrow{\mathbf{p}}_{i}) \end{aligned}\]

How to Attention

• Query Vector is Global Context Vector:

  \[\begin{aligned} \overrightarrow{\mathbf{h}} \end{aligned}\]

• Key Vector is Generated by Affection Network:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i}^{\text{(AFFECT)}} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{u}}_{u} \odot \overrightarrow{\mathbf{v}}_{i}) \end{aligned}\]

• Global Item Vector of User $u$ is Generated by:

  \[\begin{aligned} \overrightarrow{\mathbf{x}}_{u} &= \sum_{j \in \mathcal{R}_{u}^{+} \setminus \{i\}}{\alpha_{u,j} \cdot \overrightarrow{\mathbf{q}}_{j}} \end{aligned}\]

• Attention Weight is Calculated by Smoothed Softmax:

  \[\begin{aligned} \alpha_{u,j} &= \frac{\exp{f(\overrightarrow{\mathbf{h}},\overrightarrow{\mathbf{z}}_{u,j}^{\text{(AFFECT)}})}}{\left[\sum_{j \in \mathcal{R}_{u}^{+} \setminus \{i\}}{\exp{f(\overrightarrow{\mathbf{h}},\overrightarrow{\mathbf{z}}_{u,j}^{\text{(AFFECT)}})}}\right]^{\beta}} \end{aligned}\]
  • $0 < \beta \le 1$: Smoothing Factor

• Attention Score Function is Dot Product:

  \[\begin{aligned} f(q,k) &= q \cdot k \end{aligned}\]

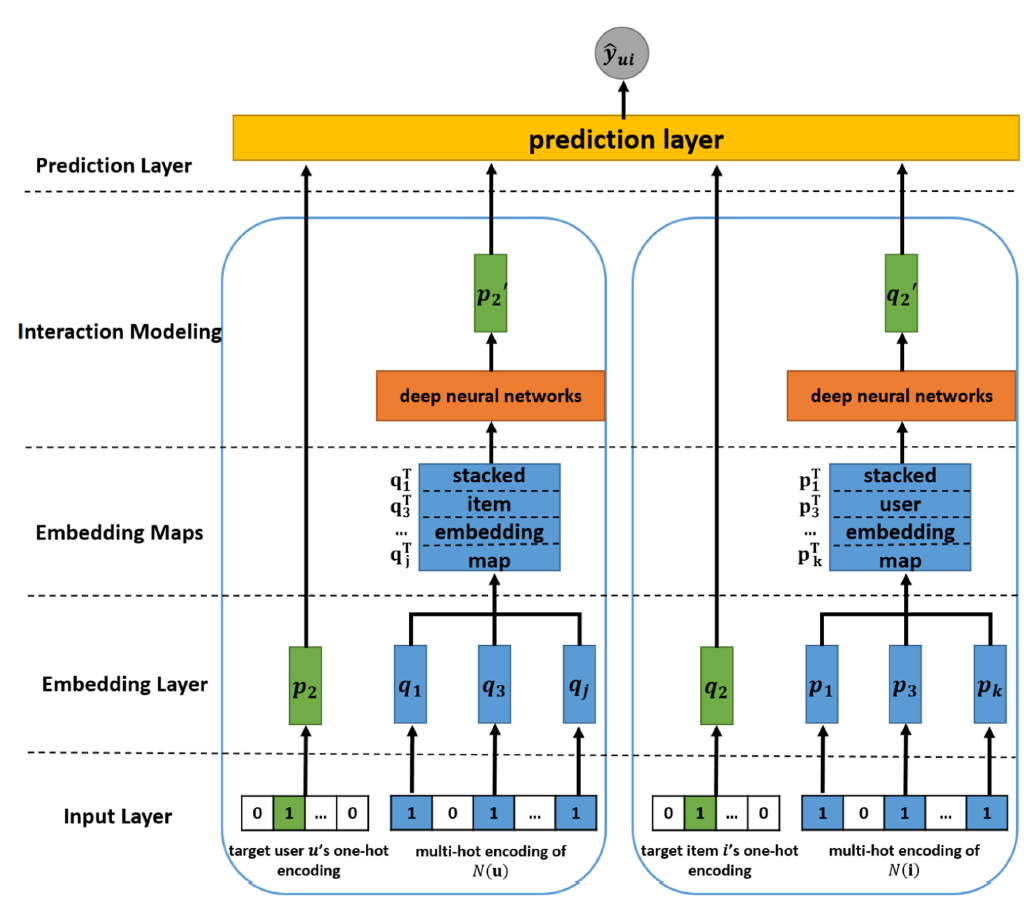
DELF: Aggregate User & Item’s Histories

---

• 문제 의식: 아이디 임베딩(ID Embedding)과 히스토리 임베딩(History Embedding)의 상호 보완적 관계
  • 아이디 임베딩은 고유 정보를 보존한 표현을 생성하는 데 강점
  • 히스토리 임베딩은 맥락 정보를 반영한 표현을 생성하는 데 강점
• DELF(Dual Embedding based Deep Latent Factor Model): 사용자와 아이템의 아이디 임베딩과 히스토리 임베딩을 조합하여 다양한 매칭 함수를 병렬 학습하는 모형
  • Cheng, W., Shen, Y., Zhu, Y., & Huang, L.
    (2018, July).
    DELF: A dual-embedding based deep latent factor model for recommendation.
    In IJCAI (Vol. 18, pp. 3329-3335).

Notation

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\mathbf{R} \in \mathbb{R}^{M \times N}$: user-item interaction matrix
• $\overrightarrow{\mathbf{p}}_{u} \in \mathbb{R}^{K}$: user ID embedding vector
• $\overrightarrow{\mathbf{q}}_{i} \in \mathbb{R}^{K}$: item ID embedding vector
• $\overrightarrow{\mathbf{m}}_{u} \in \mathbb{R}^{K}$: user history embedding vector
• $\overrightarrow{\mathbf{n}}_{i} \in \mathbb{R}^{K}$: item history embedding vector
• $\overrightarrow{\mathbf{z}}_{u,i}$: predictive vector of user $u$ and item $i$
• $\hat{y}_{u,i}$: interaction probability of user $u$ and item $i$

How to Modeling

• ID Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u} &=\text{Emb}(u)\\ \overrightarrow{\mathbf{q}}_{i} &=\text{Emb}(i) \end{aligned}\]

• History Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{m}}_{u} &=\text{ATTN}(\overrightarrow{\mathbf{h}}^{\text{(user)}}, \mathbf{H}[\forall j \in \mathcal{R}_{u}^{+} \setminus \{i\},:], \mathbf{Y}[\forall j \in \mathcal{R}_{u}^{+} \setminus \{i\},:])\\ \overrightarrow{\mathbf{n}}_{i} &=\text{ATTN}(\overrightarrow{\mathbf{h}}^{\text{(item)}}, \mathbf{H}[\forall v \in \mathcal{R}_{i}^{+} \setminus \{u\},:], \mathbf{X}[\forall v \in \mathcal{R}_{i}^{+} \setminus \{u\},:]) \end{aligned}\]

• Pairwise Neural Interaction Layers:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i}^{(1)} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{p}}_{u} \oplus \overrightarrow{\mathbf{q}}_{i})\\ \overrightarrow{\mathbf{z}}_{u,i}^{(2)} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{m}}_{u} \oplus \overrightarrow{\mathbf{n}}_{i})\\ \overrightarrow{\mathbf{z}}_{u,i}^{(3)} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{p}}_{u} \oplus \overrightarrow{\mathbf{n}}_{i})\\ \overrightarrow{\mathbf{z}}_{u,i}^{(4)} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{m}}_{u} \oplus \overrightarrow{\mathbf{q}}_{i}) \end{aligned}\]

• Predict interaction probability of user $u$ and item $i$:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot [\overrightarrow{\mathbf{z}}_{u,i}^{(1)} \oplus \overrightarrow{\mathbf{z}}_{u,i}^{(2)} \oplus \overrightarrow{\mathbf{z}}_{u,i}^{(3)} \oplus \overrightarrow{\mathbf{z}}_{u,i}^{(4)}] + \overrightarrow{\mathbf{b}}) \end{aligned}\]

How to Attention

• Another ID Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{x}}_{v} &=\text{Emb}(v)\\ \overrightarrow{\mathbf{y}}_{j} &=\text{Emb}(j) \end{aligned}\]

• Query Vector is Global Context Vector:

  \[\begin{aligned} \overrightarrow{\mathbf{h}}^{\text{(user)}}, \quad \overrightarrow{\mathbf{h}}^{\text{(item)}} \end{aligned}\]

• Key Vector is Generated by:

  \[\begin{aligned} \overrightarrow{\mathbf{h}}_{v} &= \text{tanh}(\mathbf{W} \cdot \overrightarrow{\mathbf{x}}_{v} + \overrightarrow{\mathbf{b}})\\ \overrightarrow{\mathbf{h}}_{j} &= \text{tanh}(\mathbf{W} \cdot \overrightarrow{\mathbf{y}}_{j} + \overrightarrow{\mathbf{b}}) \end{aligned}\]

• History Embedding Vector is Generated by:

  \[\begin{aligned} \overrightarrow{\mathbf{m}}_{u} &= \sum_{j \in \mathcal{R}_{u}^{+} \setminus \{i\}}{\alpha_{j} \cdot \overrightarrow{\mathbf{y}}_{j}}\\ \overrightarrow{\mathbf{n}}_{i} &= \sum_{v \in \mathcal{R}_{i}^{+} \setminus \{u\}}{\alpha_{v} \cdot \overrightarrow{\mathbf{x}}_{v}}\\ \end{aligned}\]

• Attention Weight is Calculated by Softmax:

  \[\begin{aligned} \alpha_{j} &= \frac{\exp{f(\overrightarrow{\mathbf{h}}^{\text{(user)}},\overrightarrow{\mathbf{h}}_{j})}}{\sum_{j \in \mathcal{R}_{u}^{+} \setminus \{i\}}{\exp{f(\overrightarrow{\mathbf{h}}^{\text{(user)}},\overrightarrow{\mathbf{h}}_{j})}}}\\ \alpha_{v} &= \frac{\exp{f(\overrightarrow{\mathbf{h}}^{\text{(item)}},\overrightarrow{\mathbf{h}}_{v})}}{\sum_{v \in \mathcal{R}_{i}^{+} \setminus \{u\}}{\exp{f(\overrightarrow{\mathbf{h}}^{\text{(item)}},\overrightarrow{\mathbf{h}}_{v})}}} \end{aligned}\]

• Attention Score Function is Dot Product:

  \[\begin{aligned} f(q,k) &= q \cdot k \end{aligned}\]