Latent Factor Models with CNN

ConvNCF: ID Embedding with CNN

---

• 문제 의식: NeuMF 의 다차원 고차 상호작용 포착 한계점
  • GMF 는 동일 차원 상호작용만 포착하므로 다차원 고차 상호작용 반영 불가
  • NCF 는 다양한 매칭 함수 근사 가능하나 고차원 입력 시 파라미터 수 폭증
• ConvNCF: 외적과 합성곱 신경망을 활용하여 다차원 간 고차 상호작용을 포착하는 단일 모형
  • He, X., Du, X., Wang, X., Tian, F., Tang, J., & Chua, T. S.
    (2018).
    Outer product-based neural collaborative filtering.
    arXiv preprint arXiv:1808.03912.

Notation

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\overrightarrow{\mathbf{p}}_{u} \in \mathbb{R}^{K}$: user latent factor vector
• $\overrightarrow{\mathbf{q}}_{i} \in \mathbb{R}^{K}$: item latent factor vector
• $\mathbf{E}_{u,i} \in \mathbb{R}^{K \times K}$: interaction map of user $u$ and item $i$
• $\overrightarrow{\mathbf{x}}_{u,i}$: interdimensional high-level interaction vector of user $u$ and item $i$
• $\overrightarrow{\mathbf{z}}_{u,i} \in \mathbb{R}^{K}$: predictive vector of user $u$ and item $i$
• $\hat{y}_{u,i}$: interaction probability of user $u$ and item $i$

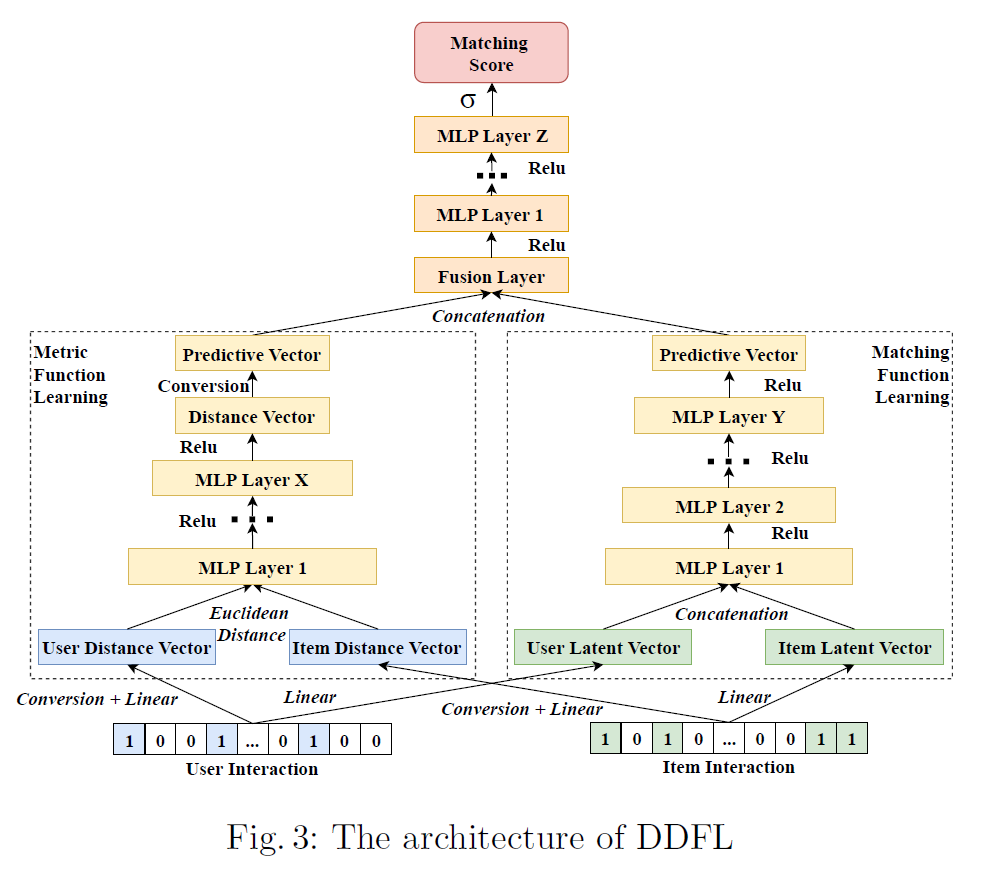
How to Modeling

• ID Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \text{Emb}(u) \in \mathbb{R}^{K}\\ \overrightarrow{\mathbf{v}}_{i} &= \text{Emb}(i) \in \mathbb{R}^{K} \end{aligned}\]

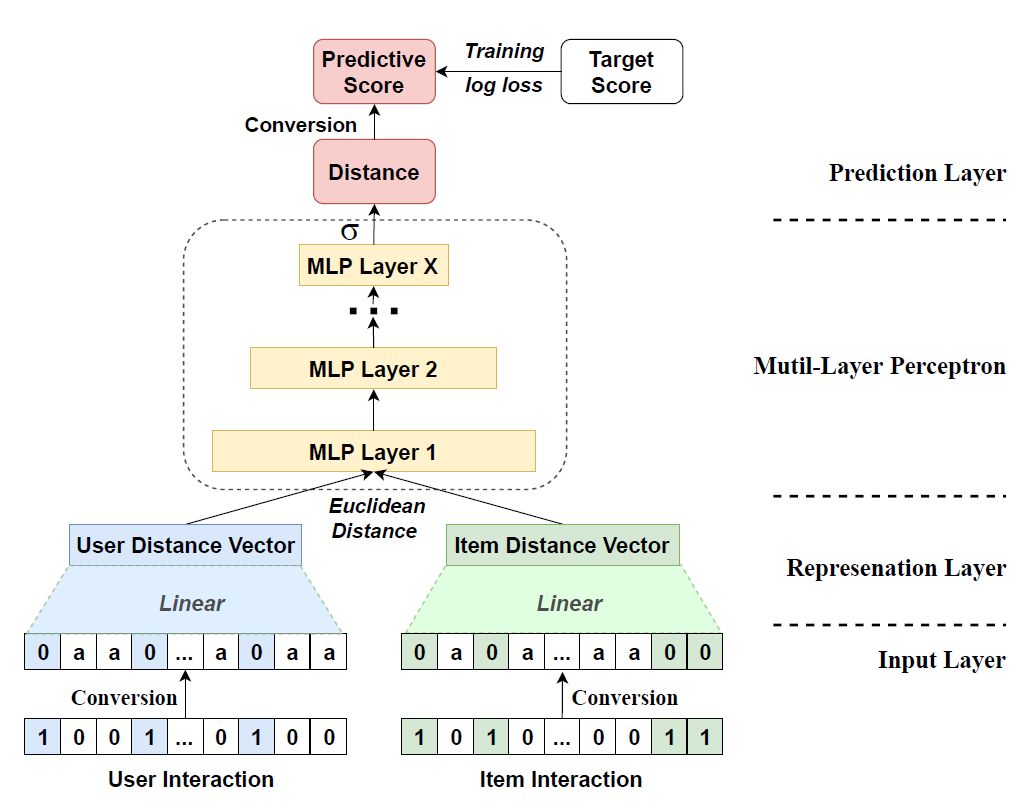
• Outer product of user $u$ and item $i$:

  \[\begin{aligned} \mathbf{E}_{u,i} &= \overrightarrow{\mathbf{u}}_{u} \otimes \overrightarrow{\mathbf{v}}_{i} \end{aligned}\]

• Capture interdimensional high-level interaction of user $u$ and item $i$:

  

  \[\begin{aligned} \overrightarrow{\mathbf{x}}_{u,i} &= \text{Flatten}\left[\text{Conv}_{\text{ReLU}}(\mathbf{E}_{u,i})\right] \end{aligned}\]
  • \(\mathcal{W} \in \mathbb{R}^{2 \times 2}\): Kernel Window Dimension
  • The number of Filters per Kernel Size is 32
  • Dimension of Feature Map is reduced $K \times K, K/2 \times K/2, \cdots, 1 \times 1$

• Predictive Vector of user $u$ and item $i$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{x}}_{u,i}) \end{aligned}\]

• Predict interaction probability of user $u$ and item $i$:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\mathbf{W} \cdot \overrightarrow{\mathbf{z}}_{u,i}) \end{aligned}\]

COMET: Dual Embedding with CNN

---

• 문제 의식: 히스토리의 다차원 고차 상호작용 구조 모델링 부재
  • 아이디 임베딩(ID Embedding): 맥락 정보 없이 목표 사용자-아이템 쌍 상호작용만을 반영함
  • 히스토리 임베딩(History Embedding): 맥락 정보를 반영하나 맥락 내 구조적 관계 정보를 모델링하지 않음
  • 실제 추천은 사용자의 히스토리 아이템 간 상호작용과, 아이템에 반응한 사용자 간 집합의 구조적 맥락에서 발생함
• COMET(COnvolutional diMEnsion inTeraction): 히스토리 간 다차원 고차 상호작용 구조를 반영한 듀얼 임베딩(Dual-Embedding) 기반 잠재요인 모형
  • Lin, Z., Feng, L., Guo, X., Zhang, Y., Yin, R., Kwoh, C. K., & Xu, C.
    (2023).
    Comet: Convolutional dimension interaction for collaborative filtering.
    ACM Transactions on Intelligent Systems and Technology, 14(4), 1-18.

Notation

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\overrightarrow{\mathbf{p}}_{u} \in \mathbb{R}^{K}$: user id embedding vector
• $\overrightarrow{\mathbf{q}}_{i} \in \mathbb{R}^{K}$: item id embedding vector
• \(\mathbf{E}_{u} \in \mathbb{R}^{\vert \mathcal{R}_{u}^{+} \setminus \{i\} \vert \times K}\): history embedding map of user $u$
• \(\mathbf{E}_{i} \in \mathbb{R}^{\vert \mathcal{R}_{i}^{+} \setminus \{u\} \vert \times K}\): history embedding map of item $i$
• $\overrightarrow{\mathbf{x}}_{u}$: history interaction vector of user $u$
• $\overrightarrow{\mathbf{x}}_{i}$: history interaction vector of item $i$
• $\overrightarrow{\mathbf{u}}_{u} \in \mathbb{R}^{K}$: user history embedding vector
• $\overrightarrow{\mathbf{v}}_{i} \in \mathbb{R}^{K}$: item history embedding vector
• $\hat{y}_{u,i}$: interaction probability of user $u$ and item $i$

How to Modeling

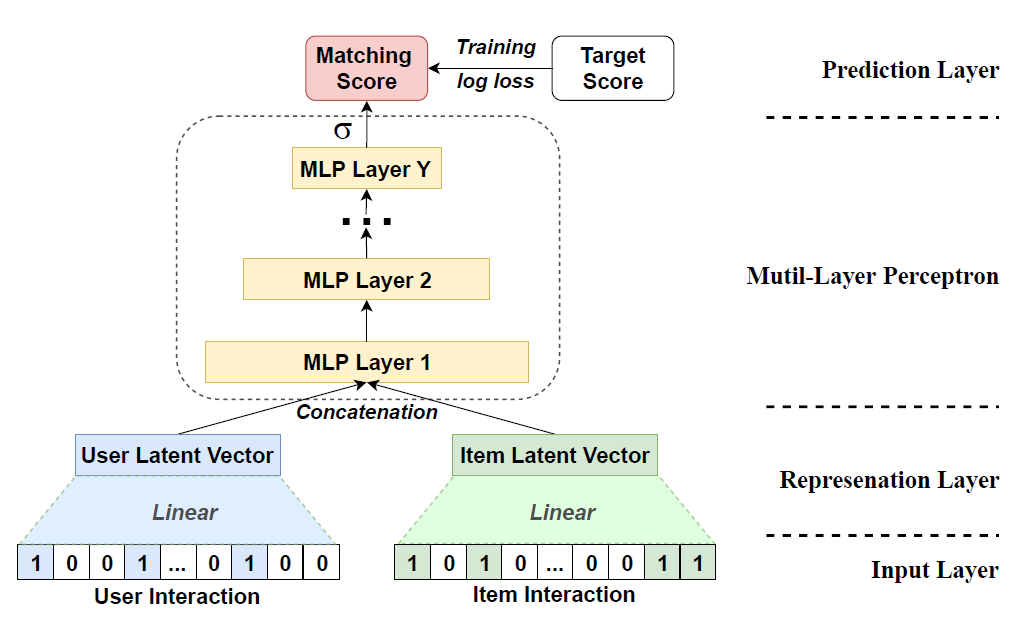
• ID Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u} &= \text{Emb}(u)\\ \overrightarrow{\mathbf{q}}_{i} &= \text{Emb}(i) \end{aligned}\]

• Interaction Modeling:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \cdots (\left\{\overrightarrow{\mathbf{q}}_{j} \mid \forall j \in \mathcal{R}_{u}^{+} \setminus \{i\}\right\})\\ \overrightarrow{\mathbf{v}}_{i} &= \cdots (\left\{\overrightarrow{\mathbf{p}}_{v} \mid \forall v \in \mathcal{R}_{i}^{+} \setminus \{u\}\right\}) \end{aligned}\]

• Predict interaction probability of user $u$ and item $i$:

  \[\begin{aligned} \hat{y}_{u,i} &= \sigma(\overrightarrow{\mathbf{w}} \cdot \left[(\overrightarrow{\mathbf{p}}_{u} + \overrightarrow{\mathbf{u}}_{u}) \odot (\overrightarrow{\mathbf{q}}_{i} + \overrightarrow{\mathbf{v}}_{i})\right]) \end{aligned}\]

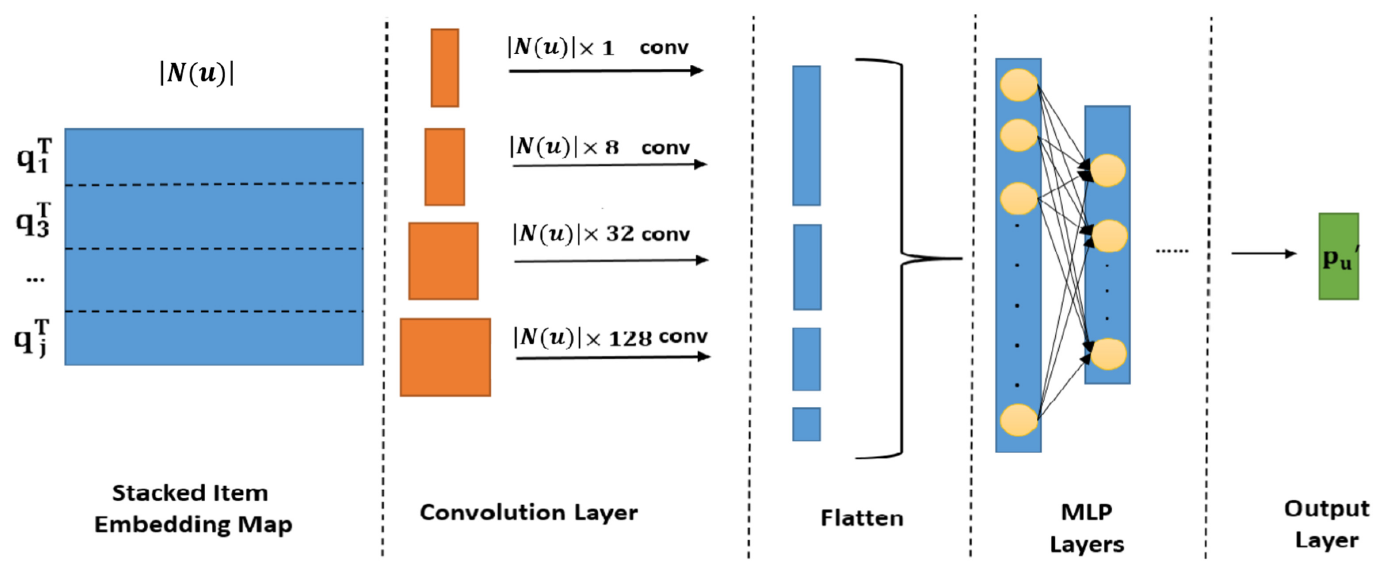
Interaction Modeling

• History Embedding Maps:

  \[\begin{aligned} \mathbf{E}_{u} = \begin{bmatrix} \overrightarrow{\mathbf{q}}_{1 \in \mathcal{R}_{u}^{+} \setminus \{i\}}\\ \overrightarrow{\mathbf{q}}_{2 \in \mathcal{R}_{u}^{+} \setminus \{i\}}\\ \vdots\\ \overrightarrow{\mathbf{q}}_{j \in \mathcal{R}_{u}^{+} \setminus \{i\}} \end{bmatrix},\quad \mathbf{E}_{i} = \begin{bmatrix} \overrightarrow{\mathbf{p}}_{1 \in \mathcal{R}_{i}^{+} \setminus \{u\}}\\ \overrightarrow{\mathbf{p}}_{2 \in \mathcal{R}_{i}^{+} \setminus \{u\}}\\ \vdots\\ \overrightarrow{\mathbf{p}}_{v \in \mathcal{R}_{i}^{+} \setminus \{u\}} \end{bmatrix} \end{aligned}\]

• CNN:

  \[\begin{aligned} \overrightarrow{\mathbf{x}}_{u} &= \text{Flatten}\left[\text{Conv}_{\text{ReLU}}(\mathbf{E}_{u})\right]\\ \overrightarrow{\mathbf{x}}_{i} &= \text{Flatten}\left[\text{Conv}_{\text{ReLU}}(\mathbf{E}_{i})\right] \end{aligned}\]
  • \(\mathcal{W} \in \mathbb{R}^{\vert \mathcal{R}^{+} \setminus \{u,i\} \vert \times H}\): Kernel Window Dimension
    • \(H \in \{1,8,32,128\}\): Kernel Window Size
    • The number of Filters per Kernel Size is 8
    • Max Pooling Applied

• Generate History Embedding:

  \[\begin{aligned} \overrightarrow{\mathbf{u}}_{u} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{x}}_{u})\\ \overrightarrow{\mathbf{v}}_{i} &= \text{MLP}_{\text{ReLU}}(\overrightarrow{\mathbf{x}}_{i}) \end{aligned}\]