Language Model

Language Model

---

• 언어 모형(Language Model) : Word Sequence(문장)에 확률을 할당하여 가장 자연스러운 문장을 탐색하는 모형

Statistical Language Model

---

SLM

• SLM(Statistical Language Model) : 조건부 확률을 활용하여 Word Sequence 발생 확률을 부여하는 모형

  \[\begin{aligned} P(W) &= P(w_1, w_2, \cdots, w_n)\\ &= \cancel{P(w_1)} \cdot \frac{\cancel{P(w_1,w_2)}}{\cancel{P(w_1)}} \cdot \frac{\cancel{P(w_1, w_2, w_3)}}{\cancel{P(w_1, w_2)}} \cdots \frac{P(w_1, w_2, \cdots, w_n)}{\cancel{P(w_1, w_2, \cdots, w_{n-1})}}\\ &= P(w_1) \cdot P(w_2 \mid w_1) \cdot P(w_3 \mid w_1, w_2) \cdots P(w_n \mid w_1, w_2, \cdots, w_{n-1})\\ &= \prod_{i=1}^{n}{P(w_i \mid w_1, w_2, \cdots, w_{i-1})} \end{aligned}\]

• 확률 부여 방법

  \[\begin{aligned} P(w_i \mid w_1, w_2, \cdots, w_{i-1}) &= \frac{\text{Count}(w_1, w_2, \cdots, w_i)}{\text{Count}(w_1, w_2, \cdots, w_{i-1})} \end{aligned}\]
  • $\text{Count}(w_1, w_2, \cdots, w_i)$ : 말뭉치에서 Word Sequence $(w_1, w_2, \cdots, w_i)$ 가 등장한 횟수

n-Gram

• n-Gram : $i$ 번째 단어를 예측함에 있어 $N-1$ 개의 단어만을 활용하는 방법

  \[\begin{aligned} P(W) &= \prod_{i=1}^{n}{P(w_{i} \mid w_{i-(n-1)}, w_{i-(n-2)}, \cdots, w_{i-1})} \end{aligned}\]

• How to Select $n$ : 통상 $n \le 5$ 권장

  Problem	Small $n$	Large $n$
  Sparsity Problem	$\downarrow$	$\uparrow$
  Long-term Dependency	$\uparrow$	$\downarrow$

  • 희소성 문제(Sparsity Problem) : 충분한 데이터를 관측하지 못하여 언어를 정확히 모델링하지 못하는 문제
  • 장기 의존성 문제(Long-term Dependency) : 문맥 내에서 멀리 떨어져 있는 단어들 간의 관계를 처리하는 문제

Neural Networks based Langauge Model

---

• 통계적 방법론의 한계점과 그 대안
  • NNLM(Neural Networks Langauge Model) : 임베딩을 활용한 희소성 문제 보완
  • RNNLM(Recurrent Neural Networks Langauge Model) : RNN 계열 레이어를 활용한 장기 의존성 문제 보완

• How to Generate a Context Vector for $w_{t+1}$

  

  • NNLM : $t$ 번째까지 등장한 단어 벡터들의 결합(Concatenation)으로 생성
  • RNNLM : $t$ 번째까지 등장한 단어 벡터들을 RNN 계열 레이어에 순차 입력하여 생성

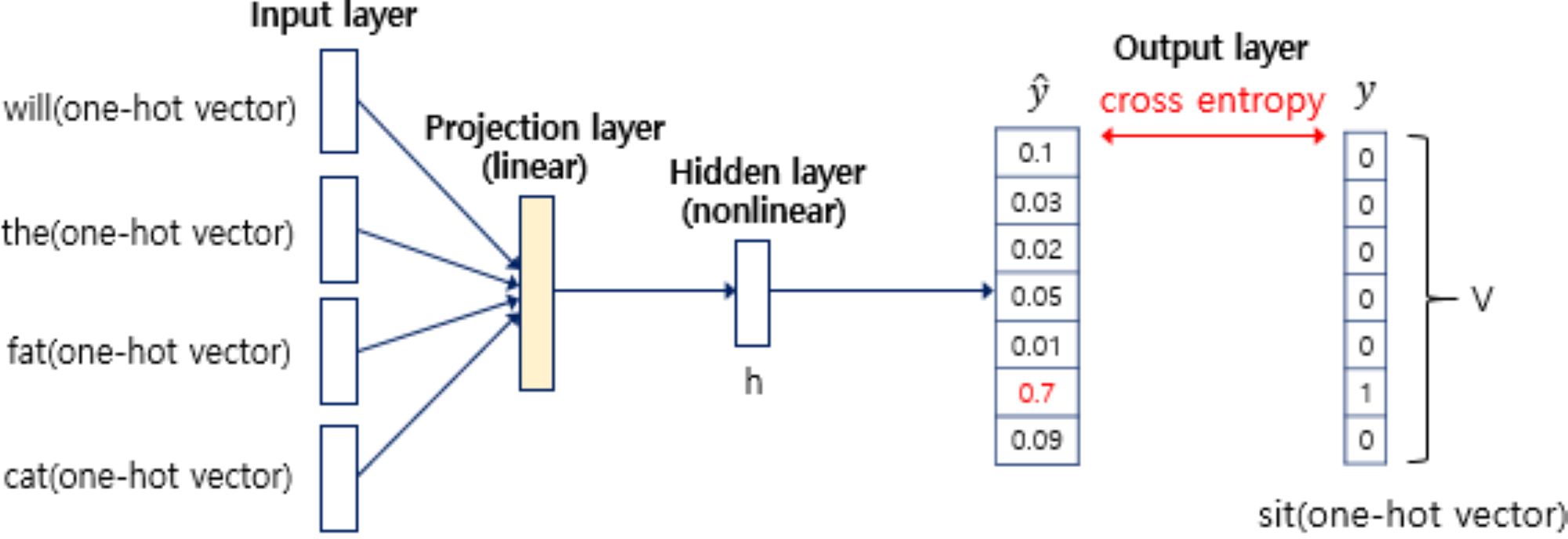
NNLM

• INPUT → PROJECTION
  • Projection : \(\overrightarrow{\mathbf{w}}_{i} = \overrightarrow{\mathbf{x}}_{i} \cdot \mathbf{W}\)
  • Concatenation : \(\overrightarrow{\mathbf{z}}_{t} = \overrightarrow{\mathbf{w}}_{t-n+1} \oplus \overrightarrow{\mathbf{w}}_{t-n+2} \oplus \cdots \oplus \overrightarrow{\mathbf{w}}_{t}\)

• PRJECTION → HIDDEN

  \[\begin{aligned} \overrightarrow{\mathbf{h}}_{t} &= \text{F}_{\text{ReLU}}\left[\overrightarrow{\mathbf{z}}_{t}\right] \end{aligned}\]

• HIDDEN → OUTPUT

  \[\begin{aligned} \hat{\mathbf{y}}_{t+1} &= \text{F}_{\text{Softmax}}\left[\overrightarrow{\mathbf{h}}_{t}\right] \end{aligned}\]

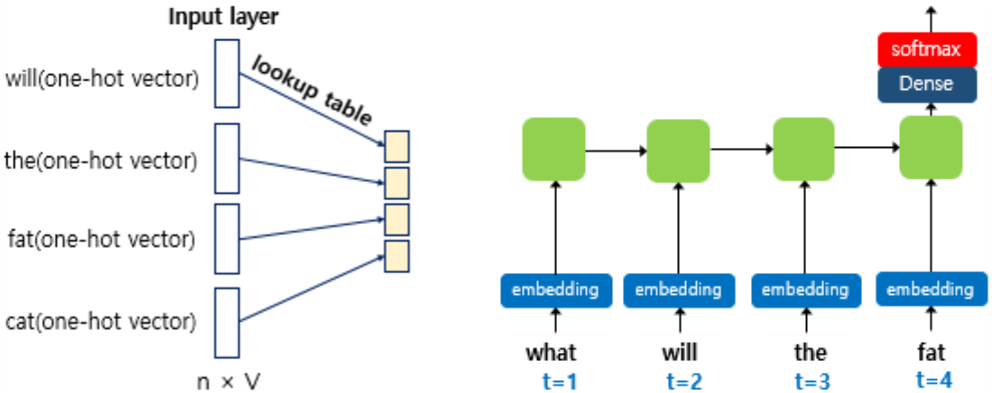
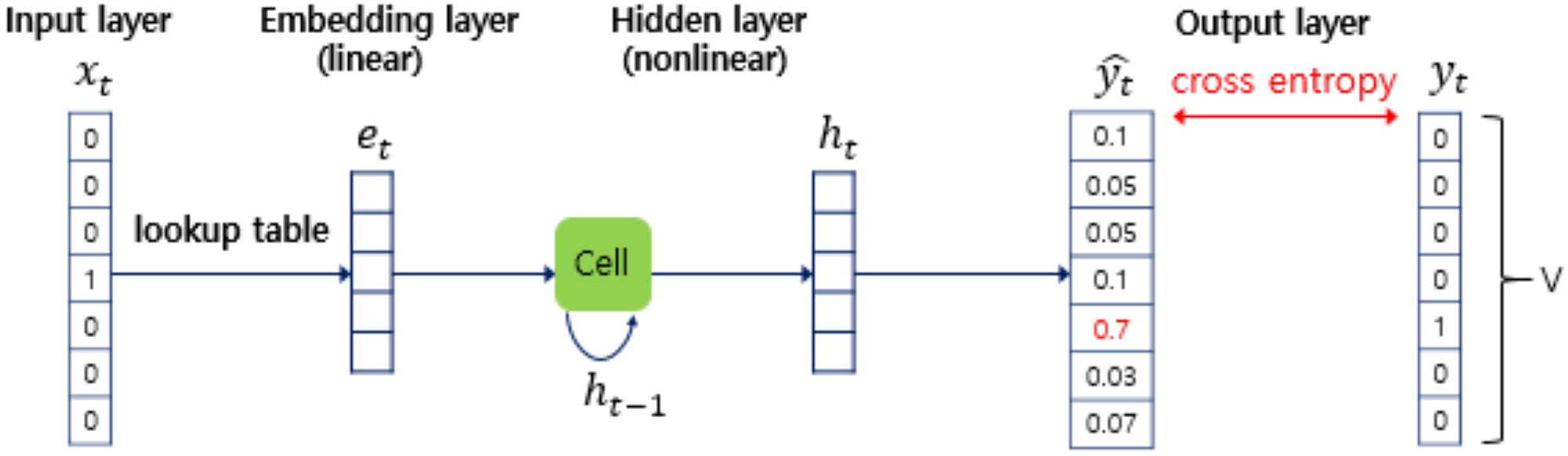
RNNLM

• INPUT → PROJECTION

  \[\overrightarrow{\mathbf{w}}_{i} = \overrightarrow{\mathbf{x}}_{i} \cdot \mathbf{W}\]

• PRJECTION → HIDDEN

  \[\begin{aligned} h_{t}, c_{t} &= \text{LSTM}\left(\overrightarrow{\mathbf{w}}_{t}, h_{t-1}, c_{t-1}\right) \end{aligned}\]

• HIDDEN → OUTPUT

  \[\begin{aligned} \hat{\mathbf{y}}_{t+1} &= \text{F}_{\text{Softmax}}\left[h_{t}\right] \end{aligned}\]

Metric

---

• PPL(PerPLexity) : 언어 모형의 성능 평가 지표

  \[\begin{aligned} PPL(W) &= P(W)^{-\frac{1}{N}}\\ &= P(w_1, w_2, \cdots, w_N)^{-\frac{1}{N}}\\ &= \sqrt[N]{\frac{1}{P(w_1, w_2, \cdots, w_N)}}\\ &= \sqrt[N]{\frac{1}{\prod_{i=1}^{n}{P(w_N \mid w_1, w_2, \cdots, w_{N-1})}}} \end{aligned}\]

• 해석 : 선택 가능한 경우의 수를 의미하는 분기 계수(Branching Factor)로서, 특정 시점마다 평균적으로 고민하는 선택지 수

  \[\begin{aligned} PPL(W) &=10\\ \sqrt[N]{\frac{1}{\prod_{i=1}^{n}{P(w_N \mid w_1, w_2, \cdots, w_{N-1})}}} &= 10\\ \prod_{i=1}^{n}{P(w_N \mid w_1, w_2, \cdots, w_{N-1})} &= \left(\frac{1}{10}\right)^{N}\\ \underset{\frac{1}{10}}{P(w_1)} \cdot \underset{\frac{1}{10}}{P(w_2 \mid w_1)} \cdot \underset{\frac{1}{10}}{P(w_3 \mid w_1, w_2)} \cdots \underset{\frac{1}{10}}{P(w_N \mid w_1, w_2, \cdots, w_{N-1})} &= \left(\frac{1}{10}\right)^{N} \end{aligned}\]