Linear Equation

Linear Equation

---

• 선형방정식(Linear Equation): 최고차항의 차수가 $1$ 을 넘지 않는 다항방정식으로서 $1$ 차 방정식

  \[\begin{aligned} a_{1}x_{1} + a_{2}x_{2} + \cdots + a_{P}x_{P} &= b \end{aligned}\]

• 선형연립방정식(Linear Simultaneous Equation): 둘 이상의 선형방정식의 집합

  \[\begin{gathered} \begin{matrix} a_{1,1}x_{1} & + & a_{1,2}x_{2} & + & \cdots & + & a_{1,P}x_{P} & = & b_1 \\ a_{2,1}x_{1} & + & a_{2,2}x_{2} & + & \cdots & + & a_{2,P}x_{P} & = & b_{2} \\ \vdots & + & \vdots & + & \ddots & + & \vdots & = & \vdots \\ a_{N,1}x_{1} & + & a_{N,2}x_{2} & + & \cdots & + & a_{N,P}x_{P} & = & b_{P} \end{matrix} \end{gathered}\]

Coefficient Matrix

---

• Vector representation of Linear Equation:

  \[\begin{gathered} \mathbf{A}\mathbf{x}=\mathbf{b} \\ \Updownarrow\\ \begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,P}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,P}\\ \vdots&\vdots&\ddots&\vdots\\ a_{N,1}&a_{N,2}&\cdots&a_{N,P} \end{bmatrix} \begin{bmatrix} x_{1}\\ x_{2}\\ \vdots\\ x_{P} \end{bmatrix} = \begin{bmatrix} b_{1}\\ b_{2}\\ \vdots\\ b_{P} \end{bmatrix} \end{gathered}\]
  • $\mathbf{A}$: 계수 행렬
  • $\mathbf{x}$: 미지수 벡터 혹은 해 벡터
  • $\mathbf{b}$: 상수 벡터

• 계수 행렬(Coefficient Matrix): 선형연립방정식 계수들의 집합으로서 벡터 $\mathbf{x}$ 를 선형변환하는 행렬

  \[\begin{aligned} \mathbf{A} &=\begin{bmatrix} a_{1,1}&a_{1,2}&\cdots&a_{1,P}\\ a_{2,1}&a_{2,2}&\cdots&a_{2,P}\\ \vdots&\vdots&\ddots&\vdots\\ a_{N,1}&a_{N,2}&\cdots&a_{N,P} \end{bmatrix} \end{aligned}\]

• 계수 행렬 \(\mathbf{A}\) 은 \(\mathbf{e}_{1},\mathbf{e}_{2},\cdots,\mathbf{e}_{P}\) 를 기저로 사용하는 좌표계에서 \(\mathbf{a}_{1},\mathbf{a}_{2},\cdots,\mathbf{a}_{P}\) 를 기저로 사용하는 좌표계로 벡터 \(\mathbf{x}\) 를 선형변환함:

  \[\begin{aligned} \mathbf{x} &=\begin{bmatrix}1 \\ 0 \\ \vdots \\ 0\end{bmatrix} x_{1} + \begin{bmatrix}0 \\ 1 \\ \vdots \\ 0\end{bmatrix} x_{2} + \cdots + \begin{bmatrix}0 \\ 0 \\ \vdots \\ 1\end{bmatrix} x_{P} \\ \mathbf{A}\mathbf{x} &= \begin{bmatrix}a_{1,1} \\ a_{2,1} \\ \vdots \\ a_{N,1}\end{bmatrix} x_{1} + \begin{bmatrix}a_{1,2} \\ a_{2,2} \\ \vdots \\ a_{N,2}\end{bmatrix} x_{2} + \cdots + \begin{bmatrix}a_{1,P} \\ a_{2,P} \\ \vdots \\ a_{N,P}\end{bmatrix} x_{P} \end{aligned}\]

Solution of the Equation

---

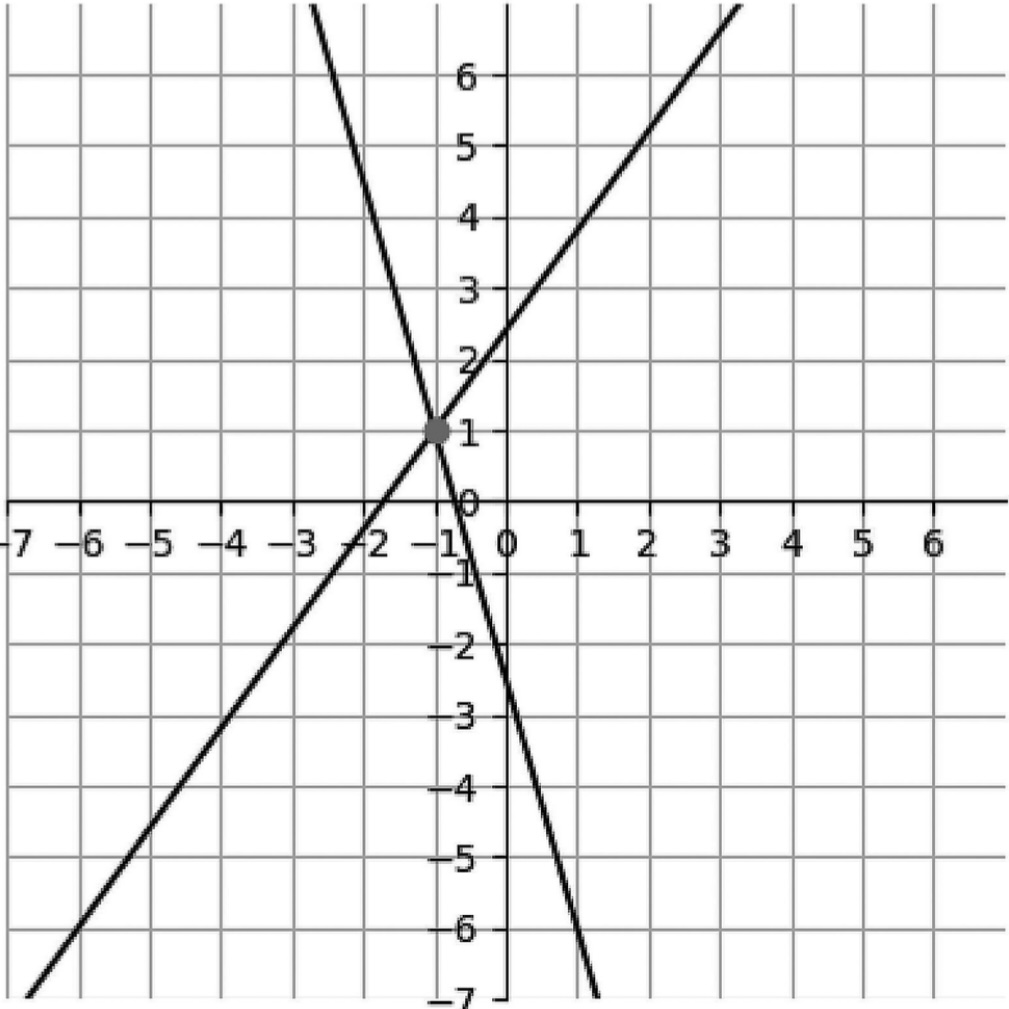
• 정해(uniquely determined): 선형연립방정식의 계수 행렬 \(\mathbf{A} \in \mathbb{R}^{N \times N}\) 에 대하여 그 역행렬이 존재하면 단 하나의 해가 존재함

  

  \[\begin{aligned} \exists \mathbf{A}^{-1} \Leftrightarrow \forall \mathbf{b} \in \mathbb{R}^{P}, \exists ! \mathbf{x} \in \mathbb{R}^{P} : \mathbf{A}\mathbf{x}=\mathbf{b} \end{aligned}\]
  • $\mathrm{rank}(\mathbf{A})=P$
  • $\mathrm{det}(\mathbf{A}) \ne 0$
  • $\sum_{i=1}^{P}{\alpha_{i}\mathbf{a}_{i}} \ne 0, \quad \forall \alpha \ne 0$
  • $\mathrm{span}(S)=\mathbb{R}^{P}, \quad S={\mathbf{a}{1},\cdots,\mathbf{a}{P}}$

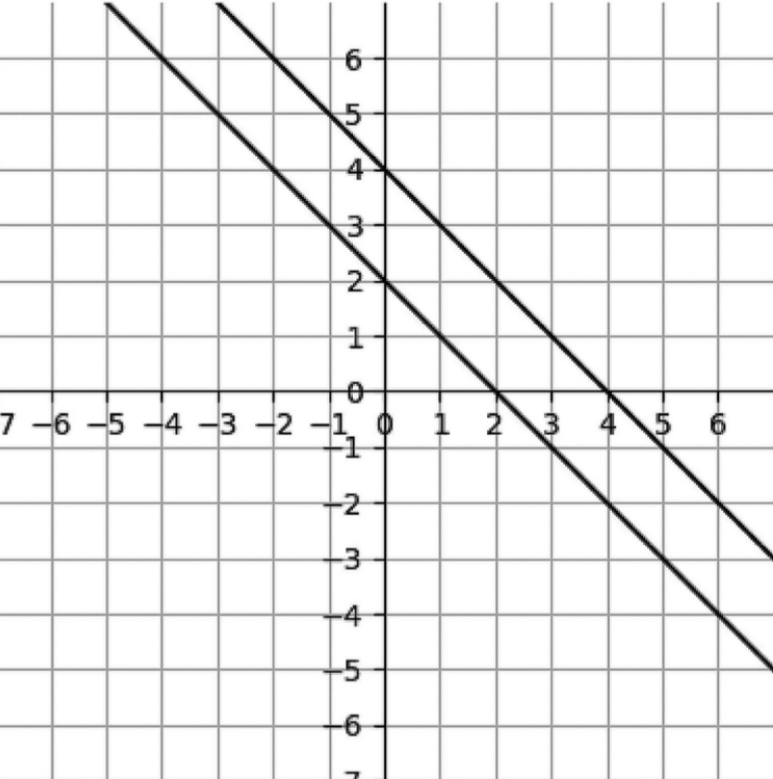
• 불능(inconsistent): 해를 구할 수 없는 상태로서, 계수 행렬 \(\mathbf{A}=\begin{bmatrix}\mathbf{a}_{1} & \mathbf{a}_{2} & \cdots & \mathbf{a}_{P}\end{bmatrix}^{T}\) 가 선형 종속이고, 동시에 \(\mathbf{b}\) 가 선형 독립인 경우

  

  \[\begin{gathered} \mathrm{rank}(\mathbf{A})<P \ \text{and} \ \mathbf{b} \notin \mathrm{span}(\{\mathbf{a}_{1},\cdots,\mathbf{a}_{P}\}) \Rightarrow \nexists \mathbf{x} \in \mathbb{R}^{P}:\mathbf{A}\mathbf{x}=\mathbf{b} \end{gathered}\]

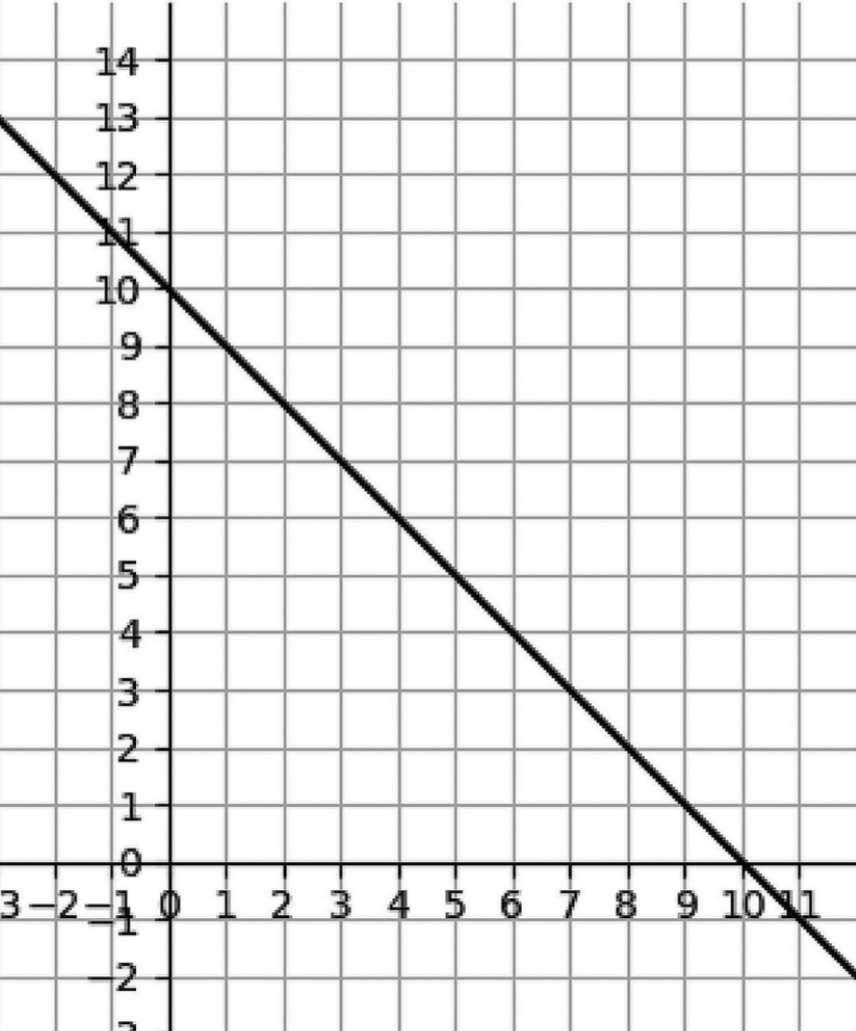
• 부정(indeterminate): 해가 무수히 많아 하나로 정할 수 없는 상태로서, 계수 행렬 \(\mathbf{A}=\begin{bmatrix}\mathbf{a}_{1} & \mathbf{a}_{2} & \cdots & \mathbf{a}_{P}\end{bmatrix}^{T}\) 가 선형 종속이고, 동시에 \(\mathbf{b}\) 도 선형 종속인 경우

  

  \[\begin{gathered} \mathrm{rank}(\mathbf{A})<P \ \text{and} \ \mathbf{b} \in \mathrm{span}(\{\mathbf{a}_{1},\cdots,\mathbf{a}_{P}\}) \Rightarrow \exists^{\infty} \mathbf{x} \in \mathbb{R}^{P}:\mathbf{A}\mathbf{x}=\mathbf{b} \end{gathered}\]