Linear Transformation

Linear Transformation

---

• 선형 변환(Linear Transformation): 행렬 $\mathbf{A} \in \mathbb{R}^{N \times P}$ 은 벡터 공간 $\mathbb{R}^{P}$ 에서 $\mathbb{R}^{N}$ 으로의 선형 사상자(Linear Map)임

  \[L: \mathbb{R}^{P} \to \mathbb{R}^{N}, \quad L(\mathbf{x}):= \mathbf{A}\mathbf{x}\]
  • $L(\mathbf{v}+\mathbf{w})=L(\mathbf{v})+L(\mathbf{w})$
  • $L(\alpha \mathbf{v})=\alpha L(\mathbf{v})$

Example

---

• 단위 행렬 \(\mathbf{I} \in \mathbb{R}^{2}\) 는 벡터 공간의 기저 벡터 \(\mathbf{e}_{1},\mathbf{e}_{2}\) 들의 집합임

  \[\begin{aligned} \mathbf{I} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} \mathbf{e}_{1} & \mathbf{e}_{2} \end{bmatrix} \end{aligned}\]

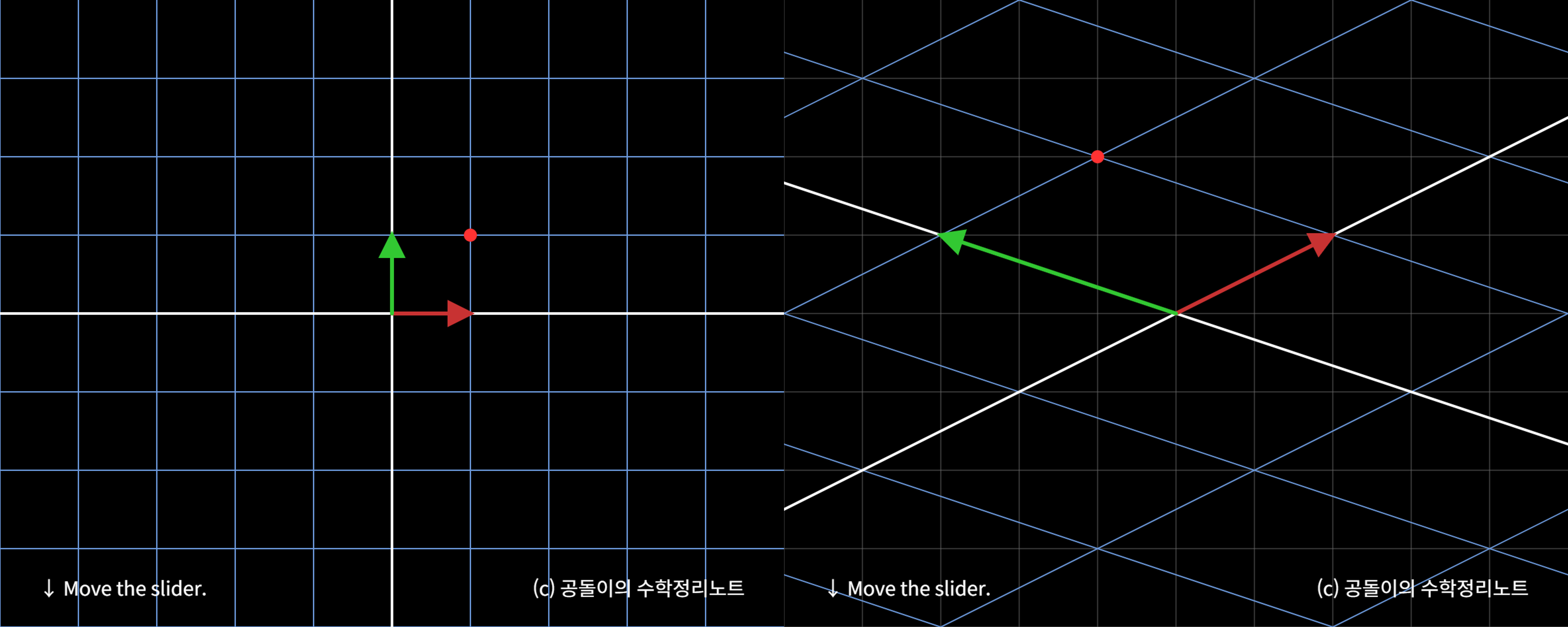
• 벡터 \(\mathbf{x} \in \mathbb{R}^{2}\) 는 \(\begin{bmatrix}1 \\0\end{bmatrix}\) 를 \(X\) 축 기저로, \(\begin{bmatrix}0 \\1\end{bmatrix}\) \(Y\) 축 기저로 취하는 좌표계에서 원점으로부터 \(X\) 축으로 \(x_{1}\) 단위, \(Y\) 축으로 \(x_{2}\) 단위 만큼 이동한 좌표임

  \[\begin{aligned} \mathbf{x} &=\begin{bmatrix}1 \\ 1\end{bmatrix} =\begin{bmatrix}1 & 0\\ 0 &1\end{bmatrix} \begin{bmatrix}1 \\ 1\end{bmatrix} =\begin{bmatrix}1 \\ 0\end{bmatrix} \cdot 1 + \begin{bmatrix}0 \\ 1\end{bmatrix} \cdot 1 \end{aligned}\]

• 행렬 $\mathbf{A}$ 는 \(X\) 축 기저 벡터를 \(\mathbf{a}_{1}\) 로, \(Y\) 축 기저 벡터를 \(\mathbf{a}_{2}\) 로 변환함

  \[\mathbf{A} =\begin{bmatrix}2 & -3\\ 1 & 1\end{bmatrix} =\begin{bmatrix}\mathbf{a}_{1} & \mathbf{a}_{2}\end{bmatrix}, \quad \begin{aligned} \mathbf{a}_{1} &=\begin{bmatrix}2 & 1 \end{bmatrix}^{T},\\ \mathbf{a}_{2} &=\begin{bmatrix}-3 & 1 \end{bmatrix}^{T} \end{aligned}\]

• 선형 변환 \(\mathbf{A}\mathbf{x}\) 는 벡터 \(\mathbf{x}\) 를 \(\mathbf{e}_{1},\mathbf{e}_{2}\) 를 기저로 취하는 죄표계에서 \(\mathbf{a}_{1},\mathbf{a}_{2}\) 를 기저로 취하는 좌표계로 사상함

  \[\begin{aligned} \mathbf{A}\mathbf{x} &= \begin{bmatrix}2 & -3\\ 1 & 1\end{bmatrix} \begin{bmatrix}1 \\ 1\end{bmatrix} =\begin{bmatrix}2 \\ 1\end{bmatrix} \cdot 1 + \begin{bmatrix}-3 \\ 1\end{bmatrix} \cdot 1 \end{aligned}\]

Special Transformation

---

• 회전 변환 행렬(Rotation Matrix): 반시계 방향으로 $\theta^{\circ}$ 회전하는 선형 변환

  \[\begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix}\]

• 크기 변환 행렬(Scaling Matrix): $X$ 축 단위를 $\alpha$ 배, $Y$ 축 단위를 $\beta$ 배 늘리는 선형 변환

  \[\begin{bmatrix} \alpha & 0 \\ 0 & \beta \end{bmatrix}\]

• 전단 변환 행렬(Shearing Matrix): 각 축의 기저 벡터를 변형시키는 선형 변환

  • Horizontal Shearing: \(X\) 축의 기저 벡터는 그대로, \(Y\) 축의 기저 벡터는 \(\begin{bmatrix} \beta \\1 \end{bmatrix}\) 으로 변형함

    \[\begin{bmatrix} 1 & \beta\\ 0 & 1 \end{bmatrix}\]

  • Vertical Shearing: \(Y\) 축의 기저 벡터는 그대로, \(X\) 축의 기저 벡터는 \(\begin{bmatrix} 1\\ \beta \end{bmatrix}\) 으로 변형함

    \[\begin{pmatrix} 1&0\\s&1 \end{pmatrix}\]

  • Arbitrary Shearing: \(X\) 축의 기저 벡터는 \(\begin{bmatrix} 1 \\ \alpha \end{bmatrix}\) 으로, \(Y\) 축의 기저 벡터는 \(\begin{bmatrix} \beta \\ 1 \end{bmatrix}\) 으로 변형함

    \[\begin{bmatrix} 1 & \beta\\ \alpha & 1 \end{bmatrix}\]

Determinant

---

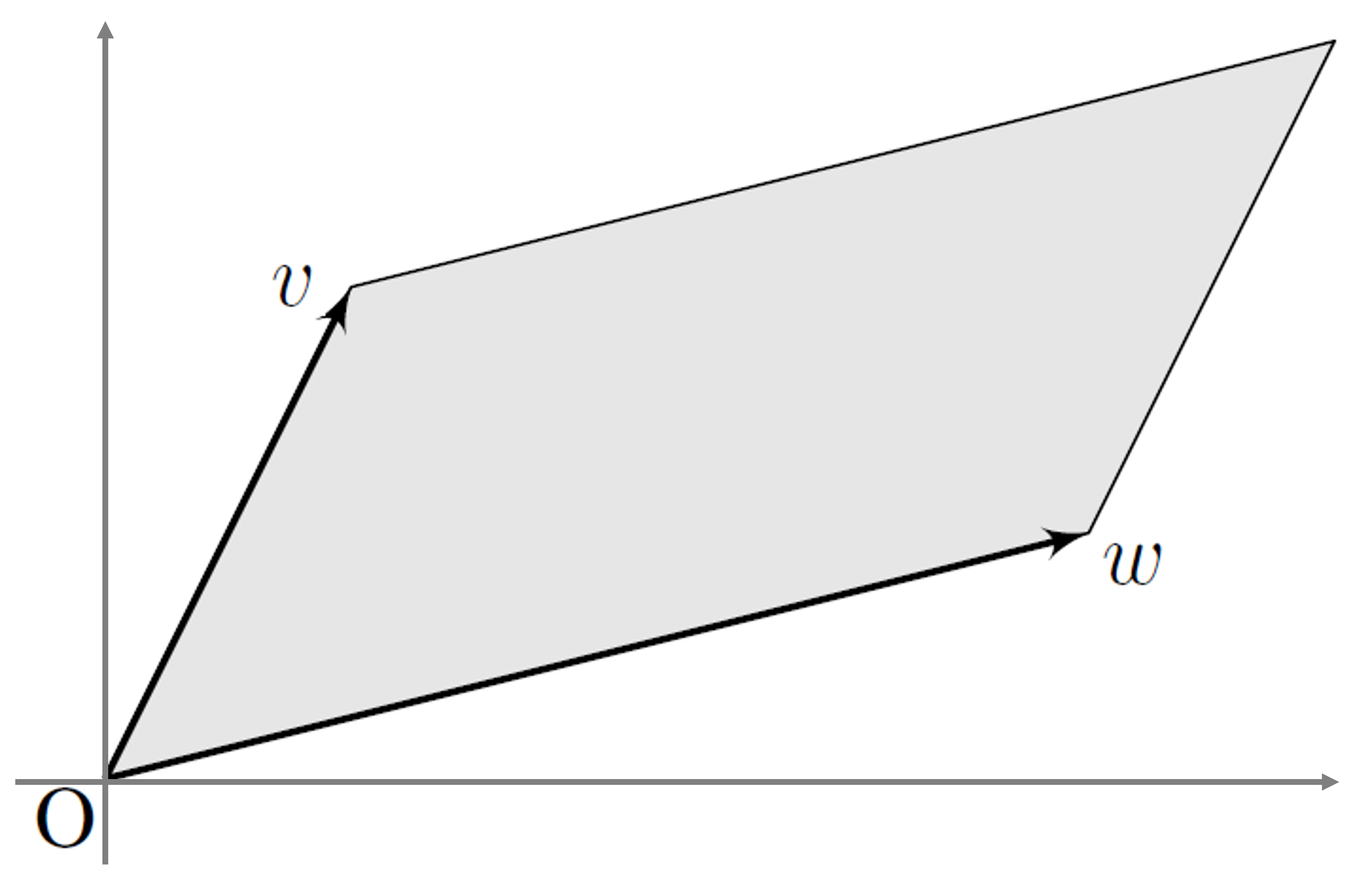
• 행렬식(Determinant): 정방행렬 \(\mathbf{A} \in \mathbb{R}^{N \times N}\) 으로 선형 변환함에 따른 좌표계 단위 면적(혹은 부피)의 변화량

  

  \[\begin{aligned} \vert\mathrm{det}(\mathbf{A}) \vert &= \Vert\mathbf{a}_{1}\Vert \cdot \Vert\mathbf{a}_{2}\Vert \cdot \sin{\theta} \end{aligned}\]
• 연산 규칙:
  • $\mathrm{det}(\alpha)=\alpha$
  • $\mathrm{det}(\alpha \mathbf{A})=\alpha^{n} \cdot \mathrm{det}(\mathbf{A})$
  • $\mathrm{det}(\mathbf{I})=1$
  • $\mathrm{det}(\mathbf{A})=\mathrm{det}(\mathbf{A}^{T})$
  • $\mathrm{det}(\mathbf{A}^{-1})=\mathrm{det}(\mathbf{A})^{-1}$
  • $\mathrm{det}(\mathbf{AB})=\mathrm{det}(\mathbf{A}) \cdot \mathrm{det}(\mathbf{B})$
  • \(\mathrm{det}(\begin{bmatrix}\mathbf{a}_{i} & \mathbf{a}_{j}\end{bmatrix}) = - \mathrm{det}(\begin{bmatrix}\mathbf{a}_{j} & \mathbf{a}_{i}\end{bmatrix})\) \(\quad\)
  • \(\mathrm{det}\left(\begin{bmatrix}\alpha \mathbf{a}_{i} \\ \mathbf{a}_{j}\end{bmatrix}\right)=\alpha \cdot \mathrm{det}\left(\begin{bmatrix}\mathbf{a}_{i} \\ \mathbf{a}_{j}\end{bmatrix}\right)\) \(\quad\)
• $\mathrm{det}(\mathbf{A})=0, \quad \mathbf{A} \in \mathbb{R}^{N \times N}$:
  • $\mathrm{rank}(\mathbf{A}) < N$
  • \(\mathrm{span}(\{\mathbf{a}_{1},\cdots,\mathbf{a}_{N}\}) \ne \mathbb{R}^{N}\) \(\quad\)
  • $\nexists \mathbf{A}^{-1}$
• $\mathrm{det}(\mathbf{A}) \ne 0, \quad \mathbf{A} \in \mathbb{R}^{N \times N}$:
  • $\mathrm{rank}(\mathbf{A}) = N$
  • \(\mathrm{span}(\{\mathbf{a}_{1},\cdots,\mathbf{a}_{N}\}) = \mathbb{R}^{N}\) \(\quad\)
  • $\exists \mathbf{A}^{-1}$

---

Sourse

• https://angeloyeo.github.io/2019/07/15/Matrix_as_Linear_Transformation.html