Logistic Regression Analysis

Prerequisite

---

• 승산(Odds) : 변수 $Y$ 가 반응할 가능성이, 반응하지 않을 가능성보다 몇 배 높은가

  \[\begin{aligned} \text{odds}(Y) &= \frac{P(Y=1)}{1-P(Y=1)} \end{aligned}\]

• 로짓(Logit; Logarithm Odds) : 승산에 로그를 취한 값

  \[\begin{aligned} \text{logit}(Y) &= \ln{\text{odds}(Y)}\\ &= \ln{\frac{P(Y=1)}{1-P(Y=1)}} \end{aligned}\]

• 승산비(Odds Ratio; OR) : 변수 $X$ 가 참일 때 $Y$ 가 반응할 가능성이, $X$ 가 거짓일 때 $Y$ 가 반응할 가능성보다 몇 배 높은가

  \[\begin{aligned} \text{OR}(Y \mid X) &= \frac{\text{odds}(Y \mid X=1)}{\text{odds}(Y \mid X=0)}\\ &= \left[\frac{P(Y=1\mid X=1)}{1-P(Y=1 \mid X=1)}\right] \bigg/ \left[\frac{P(Y=1\mid X=0)}{1-P(Y=1 \mid X=0)}\right] \end{aligned}\]
  • $\text{OR}(Y \mid X) \approx 1$ : $X$ 의 단위 변동이 $Y$ 의 승산에 영향을 미치지 않음
  • $\text{OR}(Y\mid X) < 1$ : $X$ 의 단위 변동이 $Y$ 의 승산과 음의 상관관계에 있음
  • $\text{OR}(Y \mid X) > 1$ : $X$ 의 단위 변동이 $Y$ 의 승산과 양의 상관관게에 있음

Logistic Regression

---

• 로지스틱 회귀 모형(Logistic Regression) : 범주형 반응변수에 대한 회귀 모형

  

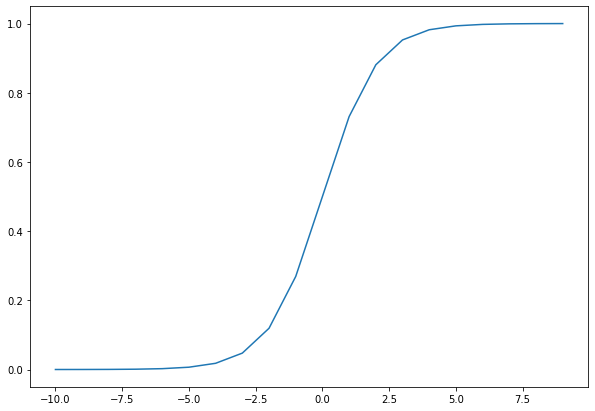
  \[P(y^{(i)}=1) = \frac{1}{1+\exp{\left[-\left(\beta_{0}+\beta_{1} \cdot x^{(i)}\right)\right]}}\]

Logistic Function

• 범주형 반응변수와 회귀식 간 범위 불일치 문제

  • 범주형 반응변수 $Y$ 의 공역

    \[y^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{true}\\ 0 \quad &\text{false} \end{aligned}\end{cases}\]

  • 회귀식의 범위

    \[\begin{aligned} f(x^{(i)}) = \beta_{0} + \beta_{1} \cdot x^{(i)} \in (-\infty,\infty) \end{aligned}\]

  • 반응변수 공역과 회귀식 범위 간 불일치

    \[\begin{aligned} y^{(i)} \ne \beta_{0} + \beta_{1} \cdot x^{(i)} \end{aligned}\]

• 반응변수 재정의를 통한 공역 조정

  • 확률 변환

    \[Y \in \{0,1\} \quad \rightarrow \quad P(Y=1) \in [0,1]\]

  • 승산(odds) 변환

    \[Y \in \{0,1\} \quad \rightarrow \quad \text{odds}(Y) \in [0,\infty)\]

  • 로짓(logit) 변환

    \[Y \in \{0,1\} \quad \rightarrow \quad \text{logit}(Y) \in (-\infty,\infty)\]

• 로지스틱 회귀식 도출

  • 로짓 변환한 반응변수와 회귀식 연결

    \[\begin{aligned} \text{logit}(y^{(i)}) &= \beta_{0} + \beta_{1} \cdot x^{(i)} \end{aligned}\]

  • 반응변수가 참일 확률에 대한 로지스틱 회귀식 도출

    \[\begin{aligned} P(y^{(i)}=1) &= \frac{1}{1+\exp\left[-\left(\beta_{0}+\beta_{1} \cdot x^{(i)}\right)\right]} \end{aligned}\]

$\beta_{1}$ related to Log Odds Ratio

• Logistic Function

  \[\ln{\frac{P(Y=1)}{1-P(Y=1)}} =\beta_0 + \beta_1 \cdot X\]

• $\text{if} \quad X=1$

  \[\begin{aligned} \ln{\frac{P(Y=1 \mid X=1)}{1-P(Y=1 \mid X=1)}} &= \beta_0 + \beta_1 \times 1 \\ &= \beta_0 + \beta_1 \end{aligned}\]

• $\text{if} \quad X=0$

  \[\begin{aligned} \ln{\frac{P(Y=1 \mid X=0)}{1-P(Y=1 \mid X=0)}} &= \beta_0 + \beta_1 \times 0 \\ &= \beta_0 \end{aligned}\]

• $\beta_1$

  \[\begin{aligned} \beta_1 &= \left(\beta_0 + \beta_1\right) - \beta_0\\ &= \ln{\frac{P(Y=1 \mid X=1)}{1-P(Y=1 \mid X=1)}} - \ln{\frac{P(Y=1 \mid X=0)}{1-P(Y=1 \mid X=0)}}\\ &= \ln{\text{odds}(Y \mid X=1)} - \ln{\text{odds}(Y \mid X=0)}\\ &= \ln{\frac{\text{odds}(Y \mid X=1)}{\text{odds}(Y \mid X=0)}}\\ &= \ln{\text{OR}(Y \mid X)} \end{aligned}\]

Maximum Liklihood Estimator

• Liklihood Function

  \[\begin{aligned} \mathcal{L}(\theta) &= \prod_{i:y=1}{P(x_{i} \mid \theta)} \cdot \prod_{j:y=0}{1-P(x_{j} \mid \theta)} \end{aligned}\]
  • $\prod_{i:y=1}{P(x_{i} \mid \theta)}$ : $\theta$ 조건부 $Y=1$ 인 관측치들이 발생할 확률
  • $\prod_{j:y=0}{1-P(x_{j} \mid \theta)}$ : $\theta$ 조건부 $Y=0$ 인 관측치들이 발생할 확률

• Maximum Liklihood Estimator

  \[\begin{aligned} \hat{\theta} &= \text{arg} \max_{\theta}{\mathcal{L}(\theta)}\\ &= \text{arg} \max_{\theta}{\prod_{i:y=1}{P(x_{i} \mid \theta)} \cdot \prod_{j:y=0}{1-P(x_{j} \mid \theta)}}\\ &= \text{arg} \max_{\theta}{\sum_{i:y=1}{P(x_{i} \mid \theta)} + \sum_{j:y=0}{P(x_{j} \mid \theta)}} \end{aligned}\]