Monte Carlo Simulation

Monte Carlo Simulation

---

• 몬테-카를로 시뮬레이션(Monte-Carlo Simulation): 복잡한 시스템이나 수학적 문제의 결과를 예측하기 위해 확률적 샘플링을 사용하는 방법

example $\Pi$

---

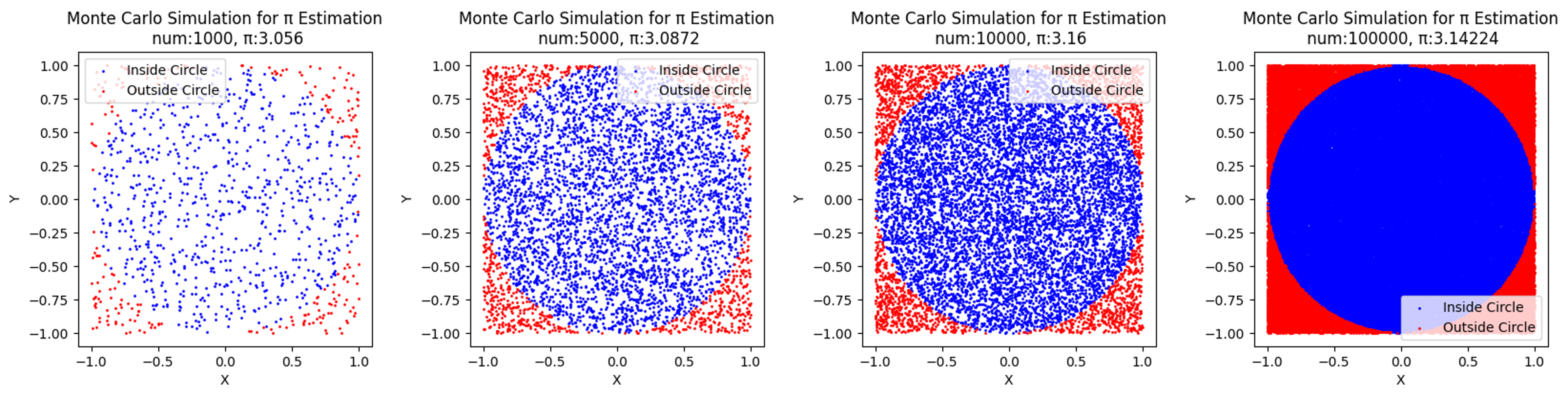
한 변의 길이가 2인 정사각형 내부에 점을 무작위로 찍었을 때, 그 점이 정사각형에 내접하는 원의 내부에 위치할 확률 실험을 전개하여, 원주율 $\pi$ 를 추론하시오.

• 좌표평면 상에서 주어진 조건을 만족하는 원:
  • 정의 \(C = \{ (x, y) \mid x^2 + y^2 = r^2 \}\)
  • 면적 $\pi r^2 = \pi \quad (\because 2r=2)$
• 좌표평면 상에서 주어진 조건을 만족하는 정사각형:
  • 정의 \(R = \{ (x, y) \mid -1 \le x \le 1, -1 \le y \le 1\}\)
  • 면적 $(2r)^2=4$

• 정사각형 내부에 점을 무작위로 찍었을 때, 점이 원 내부에 위치할 가능성:

  \[\begin{aligned} P((x,y) \in C) &=\frac{N_{circle}}{N} =\displaystyle\frac{\pi r^2}{(2r)^2} \end{aligned}\]
  • $N$ : 실행 횟수
  • $N_{circle}$ : 성공 횟수(원 내부에 위치한 횟수)

• 몬테-카를로 시뮬레이션을 통한 $\pi$ 추론값 도출:

  

  • 실행 횟수(num)가 증가할수록 $\pi$ 의 추론값이 $3.141592\cdots$ 에 근접해감

Rejection Sampling

---

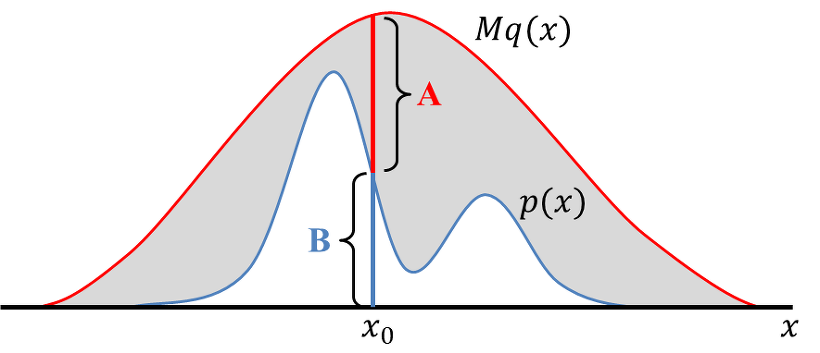
• 기각 샘플링(Rejection Sampling) : 제안 분포로부터 추출한 관측치를 기각하는 과정을 반복하여 제안 분포를 목표 분포와 유사한 형태로 만드는 방법

• Target Dist.:

  \[\begin{aligned} p(\theta \mid \mathcal{D}) \propto p(\mathcal{D} \mid \theta) \cdot p(\theta) \end{aligned}\]

• Proposed Dist.:

  \[\begin{aligned} q(\theta) \end{aligned}\]
  • $q(\theta)$ must be similar in location and distribution to $p(\theta \mid \mathcal{D})$
  • $p(\theta \mid \mathcal{D}) \le M \cdot q(\theta) \quad \text{for} \quad \forall \theta$

• Rejection Rule:

  \[\begin{aligned} \text{Accept} \quad \phi \quad \text{if} \quad u \le \frac{p(\phi \mid \mathcal{D})}{M \cdot q(\phi)} \quad \text{where} \quad u \sim \text{Uniform}(0,1) \end{aligned}\]