Multi Armed Bandits

What? Multi-Armed Bandits

---

• Multi-Armed Bandits Problem : 보상 확률을 알 수 없는 여러 선택지 중 하나를 선택하는 문제

  

  $n$ 개의 슬롯 머신이 각각 특정한 확률분포를 따르는 보상을 돌려준다고 하자. 즉, 슬롯 머신이 돌려주는 보상 금액은 동일하되, 보상 받을 확률은 다르다. 단, 슬롯 머신의 보상 확률은 알려져 있지 않다. 어떤 슬롯 머신을 고르는 것이 이득일까?

• A/B Test vs. MAB

  

  • A/B Test : 탐색 후 그 결과를 100% 활용하는 불연속적인(Discrete) 방법

    $n$ 개의 집단에 $n$ 개의 선택지를 노출하여 순수하게 새로운 가능성을 탐색(Exploration)한 후, 의사결정이 완료된 후에는 채택된 선택지를 모든 집단에 노출하여 활용함(Exploitation)

  • MAB : 탐색과 활용을 동시에 수행하는 연속적인(Continuous) 방법

    고객의 피드백을 실시간으로 반영하며 각 선택지의 보상 확률을 갱신함으로써 열등한 선택지는 비교적 적게 노출하고 우월한 선택지는 비교적 많이 노출함

• Selection Issue : Exploration-Exploitation Trade-off

  

  만약 적당히 좋은 결과를 돌려주는 슬롯 머신을 찾아냈다면, 그 결과를 유지하기 위해 그 슬롯 머신을 활용할 것인가(Exploitation) 아니면 더 좋은 결과를 얻을 수 있다는 희망으로 다른 슬롯 머신을 탐색할 것인가(Exploration)?

  • 탐색(Exploration) : 다양한 슬롯 머신들을 선택하면서 보상이 어느 정도 도출되는지 탐색하는 과정
  • 활용(Exploitation) : 수집된 정보를 바탕으로 보상 확률이 높은 슬롯 머신을 선택하는 과정

Selection Algorithms

---

• Loss Function for MAB is Total Regret

  \[\begin{aligned} \mathcal{R}(T) &= \sum_{t=1}^{T}{\left[\theta_{opt}-\theta_{B(t)}\right]}\\ &= T \cdot \theta_{opt} - \sum_{t=1}^{T}{\theta_{B(t)}} \end{aligned}\]
  • $B(t)$ : $t$ 번째 시점에서 선택한 슬롯 머신
  • $P_{B(t)}$ : $t$ 번째 시점에서 선택한 슬롯 머신의 보상 확률 분포
  • $\theta_{B(t)} \sim P_{B(t)}$ : $t$ 번째 시점에서 선택한 슬롯 머신의 보상 확률
  • $\theta_{opt}$ : 최적 슬롯 머신의 보상 확률

Bayes Selection; Thompson Sampling

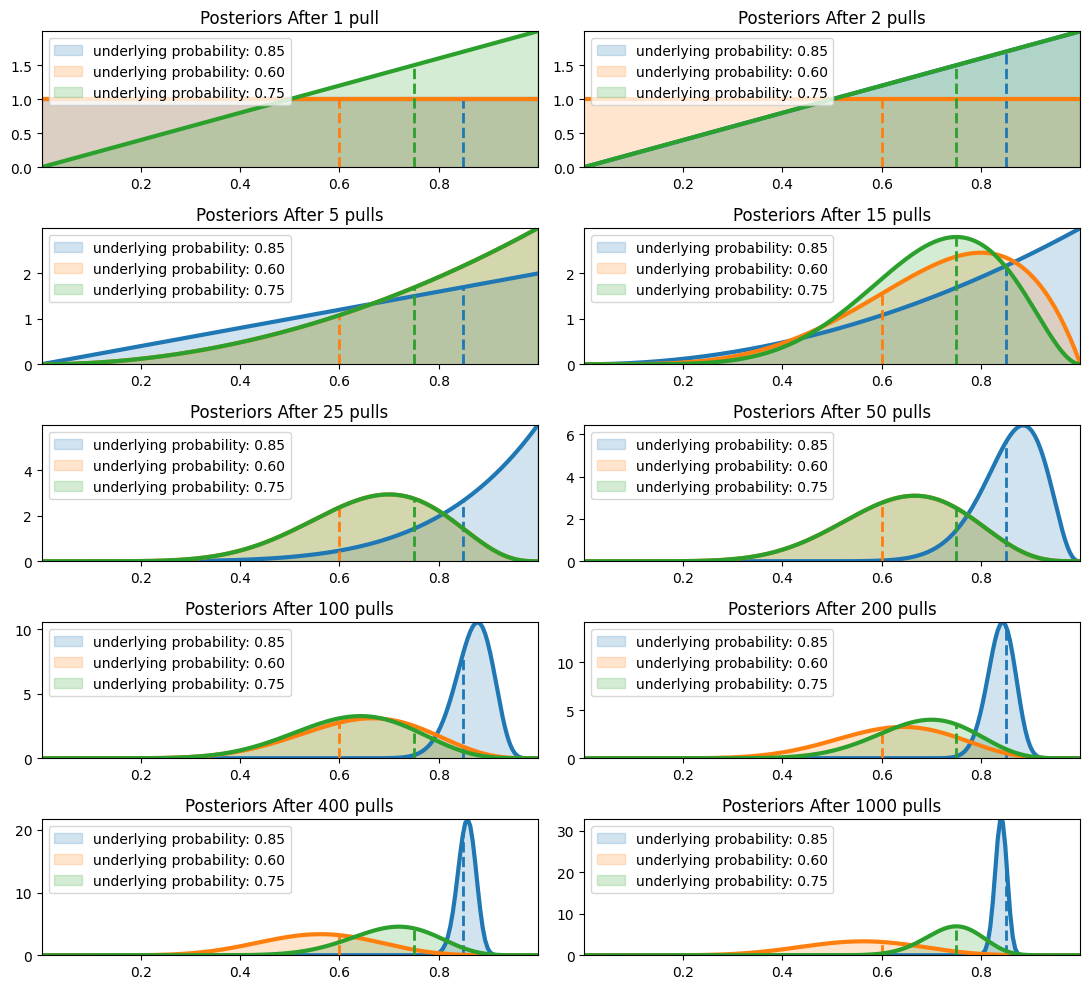
1. 모든 슬롯 머신의 보상 확률에 대하여 사전 확률 분포 설정

   \[\begin{aligned} X \mid \theta &\sim \text{Bin}(n,\theta)\\ \therefore \theta &\sim \text{Beta}(\alpha_0,\beta_0) \end{aligned}\]

2. 보상 확률이 가장 높은 슬롯 머신 선택

   \[B(t)=\text{arg}\max_{a}{\theta_{a}}\]

3. 보상 관찰 후 해당 슬롯 머신의 사후 확률 분포 갱신

   \[\begin{aligned} \theta_{B(t)} \mid X &\sim \text{Beta}(\alpha, \beta)\\ \alpha &= \alpha_0 + X\\ \beta &= \beta_0 - n + X \end{aligned}\]

Extra Selection Algorithms

• Greedy : $t-1$ 번째 시점까지 탐색한 정보를 토대로 기대 보상이 가장 큰 슬롯 머신만을 활용하는 전략

  \[\begin{aligned} B(t) &= \text{arg}\max_{a}{Q(a;t)}\\ &= \text{arg}\max_{a}{\frac{\sum_{i=1}^{t-1}{\tau_{i} \cdot \mathbb{I}\left[B(i)=a\right]}}{\sum_{i=1}^{t-1}{\mathbb{I}\left[B(i)=a\right]}}} \end{aligned}\]
  • $\tau_{i}$ : $i$ 번째 시점에서 받은 보상
  • $\mathbb{I}\left[B(i)=a\right]$ : Indicate Function

• $\varepsilon$-Greedy : $\varepsilon$ 의 확률로 새로운 슬롯 머신을 탐색하는 전략

  \[B(t) = \begin{cases}\begin{aligned} Q(a;t) \quad & \text{with probability} \; 1-\varepsilon\\ \text{random} \quad & \text{with probability} \; \varepsilon \end{aligned}\end{cases}\]
  • $Q(a;t)$ : Exploitation Term
  • $\text{random}$ : Exploration Term

• UCB(Upper Confidence Bound) : 승률이 높은 슬롯 머신을 활용하면서, 승률의 불확실성이 높은 슬롯 머신을 탐색하는 전략

  \[B(t) =\text{arg}\max_{a}{\left[Q(a;t) + c \cdot \sqrt{\frac{\ln{t}}{\sum_{i=1}^{t-1}{\mathbb{I}\left[B(i)=a\right]}}}\right]}\]
  • $Q(a;t)$ : Exploitation Term
  • $\sqrt{\displaystyle\frac{\ln{t}}{\sum_{i=1}^{t-1}{\mathbb{I}\left[B(i)=a\right]}}}$ : Exploration Term
  • $c$ : Exploration Constant

---

이미지 출처

• https://multithreaded.stitchfix.com/blog/2020/08/05/bandits/
• https://link.springer.com/article/10.1007/s10489-023-04955-0?fromPaywallRec=false