Multiple Linear Regression Analysis

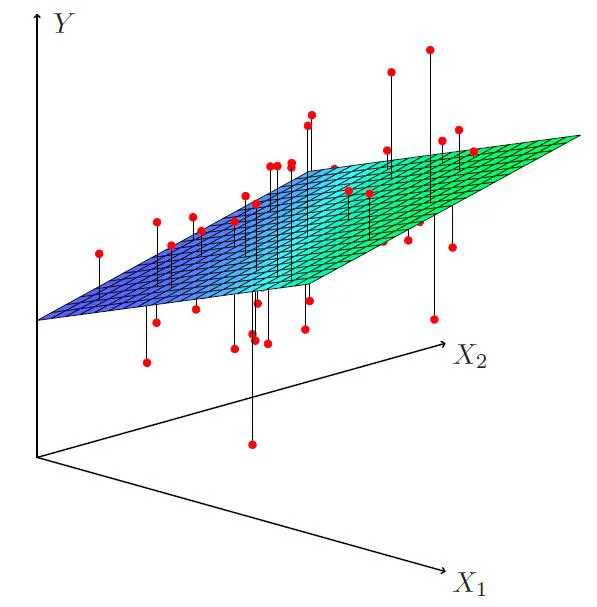
What? Multiple Linear Regression

---

• 정의 : 설명변수가 여러 개인(Multi-Variate) 선형 회귀 모형(Linear Regression Model)

  

  \[y^{(k)}=\beta_{0}+\beta_{1}x_{1}^{(k)}+\beta_{2}x_{2}^{(k)}+\cdots+\beta_{p}x_{p}^{(k)}+\varepsilon^{(k)}\]

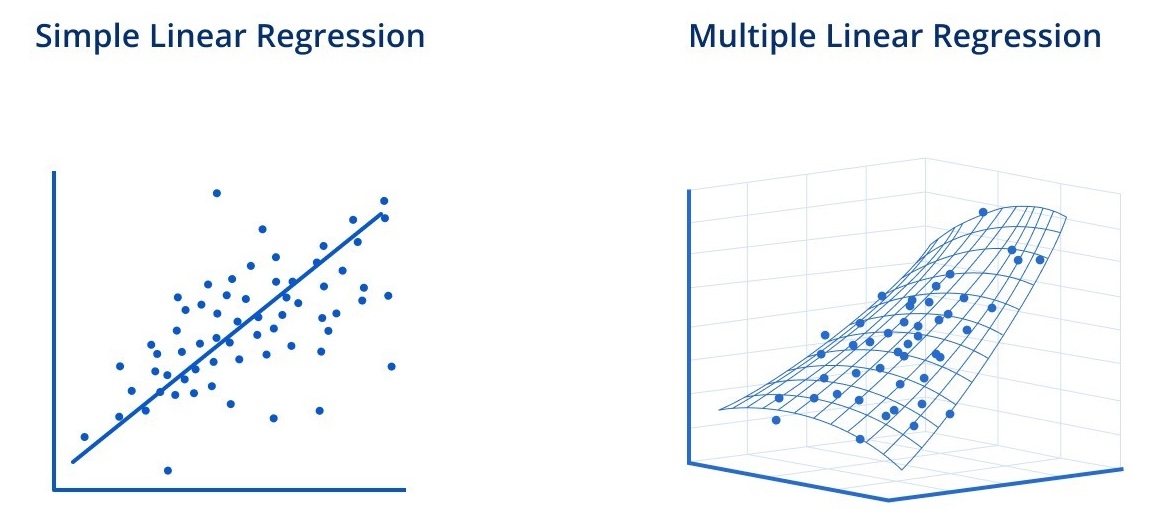
• VS. Simple Linear Regression

  

  • Simple Linear Regression

    \[\begin{aligned} \text{Sales}^{(k)} &=\beta_{0}+\beta_{1} \cdot \text{TV}^{(k)}+\varepsilon^{(k)}\\ \text{Sales}^{(k)} &=\beta_{0}+\beta_{2} \cdot \text{Radio}^{(k)}+\varepsilon^{(k)}\\ \text{Sales}^{(k)} &=\beta_{0}+\beta_{3} \cdot \text{News}^{(k)}+\varepsilon^{(k)} \end{aligned}\]

    회귀계수 $\beta_{i}$ 은 다른 요인($X_{j \ne i}$)들의 변화에 따른 매출($\text{Sales}$)의 변동성을 통제하지 않은 상태에서 추정되었다. 때문에 해당 요인($X_{i}$)과 다른 요인들 간 상관관계가 있을 경우, $\beta_{i}$ 은 다른 요인들의 변화가 매출에 미치는 영향력을 포함하게 된다. 따라서 $\beta_{i}$ 은 $X_{i}$ 가 $\text{Sales}$ 에 미치는 순수한 영향력이라 볼 수 없다.

  • Multiple Linear Regression

    \[\text{Sales}^{(k)}=\beta_{0}+\beta_{1} \cdot \text{TV}^{(k)}+\beta_{2} \cdot \text{Radio}^{(k)}+\beta_{3} \cdot \text{News}^{(k)}+\varepsilon^{(k)}\]

    회귀계수 $\beta_{i}$ 은 다른 요인($X_{j \ne i}$)들의 변화에 따른 매출($\text{Sales}$)의 변동성을 통제한 상태에서 추정되었다. 따라서 $\beta_{i}$ 은 $X_{i}$ 가 $\text{Sales}$ 에 미치는 순수한 영향력이라 볼 수 있다.

Normal Equation

---

• 정규방정식(Normal Equation) : 최소자승법에 기초하여 추정한 가중치 벡터

  \[\begin{aligned} \hat{\overrightarrow{\beta}} &= \text{arg} \min_{\overrightarrow{\beta}}{RSS}\\ &= (\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\overrightarrow{y} \end{aligned}\]
• 정규방정식 도출 과정

  • 변수 갯수가 $P$ 이고 관측치 갯수가 $N$ 인 다중 선형 회귀 모형을 선형대수로 표현하면 다음과 같음

    \[\overrightarrow{\hat{y}} = \mathbf{X}\hat{\overrightarrow{\beta}}\]
    • $\mathbf{X}_{N \times P}$ : Design Matrix

  • $RSS$ 도출

    \[\begin{aligned} RSS &= \left\Vert \overrightarrow{y} - \overrightarrow{\hat{y}} \right\Vert^2\\ &= (\overrightarrow{y}^T - \overrightarrow{\beta}^T \mathbf{X}^T)(\overrightarrow{y} - \mathbf{X}\overrightarrow{\beta})\\ &= \overrightarrow{y}^T \overrightarrow{y} - \overrightarrow{y}^T \mathbf{X} \overrightarrow{\beta} - \overrightarrow{\beta}^T \mathbf{X}^T \overrightarrow{y} + \overrightarrow{\beta}^T \mathbf{X}^T \mathbf{X} \overrightarrow{\beta} \end{aligned}\]

  • $\because \overrightarrow{y}^T \mathbf{X} \overrightarrow{\beta} = \left(\overrightarrow{\beta}^T \mathbf{X}^T \overrightarrow{y}\right)^T = \overrightarrow{\beta}^T \mathbf{X}^T \overrightarrow{y}$

    \[RSS = \overrightarrow{y}^T \overrightarrow{y} - 2 \overrightarrow{\beta}^T \mathbf{X}^T \overrightarrow{y} + \overrightarrow{\beta}^T \mathbf{X}^T \mathbf{X} \overrightarrow{\beta}\]

  • $RSS$ 를 $\overrightarrow{\beta}$ 에 대하여 편미분

    \[\begin{aligned} \frac{\partial}{\partial \overrightarrow{\beta}} RSS &= -2 \mathbf{X}^T \overrightarrow{y} + 2 \mathbf{X}^T \mathbf{X} \overrightarrow{\beta}\\ &= 0 \quad (\because \min_{\overrightarrow{\beta}}{RSS}) \end{aligned}\]

  • $\overrightarrow{\beta}$ 에 대하여 정리

    \[\begin{aligned} \hat{\overrightarrow{\beta}} &= (\mathbf{X}^{T}\mathbf{X})^{-1}\mathbf{X}^{T}\overrightarrow{y}\\ &= \text{arg} \min_{\overrightarrow{\beta}}{RSS} \end{aligned}\]

• 회귀계수의 해석

  설명변수 $X_{i}$ 의 회귀계수 $\beta_{i}$ 는 다른 모든 설명변수가 일정할 때 $X_{i}$ 가 $1$ 단위 변화함에 따른 $Y$ 변화 단위의 추정치이다. 즉, 다른 모든 설명변수에 대하여 변동이 없는 상태에서, $X_{i}$ 가 $1$ 단위 변화했을 때 $Y$ 가 $\beta_{i}$ 만큼 변화할 것이라 추정된다.

회귀계수의 유의성 검정: F-검정

---

• 정의 : 반응변수에 대한 설명변수들의 설명력이 통계적으로 유의한가에 관한 검정

• 귀무가설과 대립가설 설정
  • $H_{0}: \quad \beta_1=\beta_2 =\cdots =\beta_p=0$
  • $H_{1}: \quad$ 적어도 하나의 $i$ 에 대하여 $\beta_{i} \ne 0$

• 검정통계량 도출

  \[F = \frac{ESS/p}{RSS/(n-p-1)} \sim F(p, n-p-1)\]

  • 회귀변동(Explained Sum of Square; ESS) : 모형에 의해 설명되는 반응변수의 변동성

    \[ESS=TSS-RSS\]

  • 총변동(Total Sum of Square; TSS) : 반응변수의 총 변동성

    \[\begin{aligned} TSS &= \left\Vert \overrightarrow{y} - \overline{y} \right\Vert^2\\ &= \sum{\left(y^{(i)}-\overline{y} \right)^2} \end{aligned}\]

  • 잔차변동(Residual Sum of Square) : 모형에 의해 설명되지 않는 반응변수의 변동성

    \[\begin{aligned} RSS &= \left\Vert \overrightarrow{y} - \overrightarrow{\hat{y}} \right\Vert^2\\ &= \sum{\left(y^{(i)}-\hat{y}^{(i)}\right)^2} \end{aligned}\]

부분 유의성 검정

Occam’s Razor

Entities should not be multiplied beyond necessity.

• 정의 : 설명변수 추가에 따른 부분적 효과의 통계적 유의성에 관한 검정

• 모형 예시
  • $y=\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \varepsilon$
  • $y=\beta_0 + \beta_1 X_1 + \beta_2 X_2 + \beta_3 X_3 + \beta_4 X_4 + \varepsilon$
• 귀무가설과 대립가설 설정
  • $H_{0}: \quad \beta_3=\beta_4=0$
  • $H_{1}: \quad \beta_{3} \ne 0 \quad \text{or} \quad \beta_{4} \ne 0$

• 검정통계량 도출

  \[F = \frac{(RSS_{0}-RSS)/q}{RSS/(n-p-1)} \sim F(q, n-p-1)\]

  • $RSS$ : 설명변수 $X_{3}, X_{4}$ 를 추가한 모형에 의해 설명되지 않는 반응변수의 변동성

    \[\begin{aligned} RSS &= \sum{\left[y^{(i)}-\left(\beta_0 + \beta_1 x^{(i)}_1 + \beta_2 x^{(i)}_2 + \beta_3 x^{(i)}_3 + \beta_4 x^{(i)}_4 \right) \right]^2} \end{aligned}\]

  • $RSS_{0}$ : 설명변수 $X_{3}, X_{4}$ 를 추가하지 않은 모형에 의해 설명되지 않는 반응변수의 변동성

    \[\begin{aligned} RSS_{0} &= \sum{\left[y^{(i)}-\left(\beta_0 + \beta_1 x^{(i)}_1 + \beta_2 x^{(i)}_2 \right) \right]^2} \end{aligned}\]
  • $n$ : 관측치 갯수
  • $p$ : 총 설명변수 갯수
  • $q$ : 검정 대상 설명변수($X_{3}, X_{4}$) 를 제외한 설명변수의 갯수

---

이미지 출처

• https://www.linkedin.com/pulse/understanding-linear-regression-basics-divyesh-sonar-snv4c/