MLP based Latent Factor Models

Summarize Embedding Method

Type	How to	Pos	Neg
ID Embedding	사용자, 아이템 ID 임베딩을 통해 벡터 생성	사용자, 아이템의 고유한 특징 포착 가능	맥락 정보 부재로 인해 최적화 어려움
History Embedding	상호작용 이력을 기반으로 벡터 생성	사용자 행동 패턴, 아이템 구매 패턴 포착 가능	상호작용에 지나치게 의존하여 고유한 특징 포착 어려움
Dual Embedding	ID Embedding 과 History Embedding 결합	-	-
Semi-Dual Embedding	사용자, 아이템 중 한 측면에만 History Embedding 추가	-	-
Distance Embedding	ID Embedding 시 삼각 부등식을 만족하도록 거리 학습	-	-

ID Embedding Method: NCF

---

• Matrix Factorization based Latent Factor Model : 내적(Dot Product) 을 활용하는 단순 선형 접근법은 사용자와 아이템 간 상호작용 및 각각의 잠재 표현을 충분히 학습할 수 없음

• NeuMF : 선형성을 학습하는 행렬 분해 기반 모형과 비선형성을 학습하는 신경망 알고리즘 기반 모형을 결합함으로써 선형성과 비선형성을 모두 포착함

  • Neural Collaborative Filtering(2017)

How to Modeling

• GMF(Generalized Matrix Factorization) : 아다마르 곱(Element-wise Product)을 활용하여 사용자와 아이템 간 선형 상호작용 및 각각의 일반화된 잠재 표현 학습

  \[\begin{aligned} \mathbf{Y}_{\text{GMF}} &= \mathbf{P}_{\text{GMF}} \odot \mathbf{Q}_{\text{GMF}} \end{aligned}\]

• MLP(Multi-Layer Perceptron) : 벡터 결합(Vector Concatenation)과 신경망 알고리즘(Neural Network Algorithm)을 활용하여 사용자와 아이템 간 비선형 상호작용 및 각각의 복잡한 잠재 표현 학습

  \[\begin{aligned} \mathbf{Y}_{\text{MLP}} &= \text{MLP}\left[\mathbf{P}_{\text{MLP}} \oplus \mathbf{Q}_{\text{MLP}}\right] \end{aligned}\]

• NeuMF : 선형성과 비선형성을 결합하여 최종 예측값을 도출함

  \[\begin{aligned} \mathbf{Y} &= \sigma\left[\mathbf{Y}_{\text{MLP}} \oplus \mathbf{Y}_{\text{MLP}}\right] \end{aligned}\]

History Embedding Method: DeepCF

---

• Representation Learning based Collaborative Filtering : 사용자와 아이템을 공통의 잠재 공간에 사상하여 내적(Dot Product) 을 통해 유사도를 측정함
  • 내적은 선형성을 가정하므로 상호작용의 비선형성을 학습할 수 없음
  • 내적은 잠재요인 차원 간 독립성을 가정하므로 차원 간 상호작용을 학습할 수 없음
  • 내적은 모든 차원의 비중을 동일하게 취급하므로 차원 간 중요도에 차등을 둘 수 없음
• Matching Function Learning based Collaborative Filtering : 벡터 결합(Vector Concatenation)과 신경망 알고리즘(Neural Network Algorithm) 을 통해 사용자와 아이템 쌍의 복잡한 매칭 함수를 학습함
  • 사용자와 아이템 간 단순 선형 유사성이나 각각의 주요 패턴을 포착하여 일반화된 표현을 학습하기에 어려움
  • 파라미터 수가 기하급수적으로 증가하므로 데이터 희박성에 따른 차원의 저주 발생
• DeepCF(Deep Collaborative Filtering) : 표현 학습과 매칭 함수 학습을 결합함으로써 저랭크 표현 학습 효율성을 달성하는 동시에 사용자와 아이템 간 상호작용에 대한 풍부한 표현력을 확보함
  • DeepCF: A Unified Framework of Representation Learning and Matching Function Learning in Recommender System(2019)

How to Modeling

• Representation Learning : Dimension Reduction

  \[\begin{aligned} \mathbf{Y}_{\text{RL}} &= \text{MLP}_{\text{ReLU}}\left[\mathbf{R}\right] \odot \text{MLP}_{\text{ReLU}}\left[\mathbf{R}^{T}\right] \end{aligned}\]
  • \(\mathbf{R} \in \mathbb{R}^{M \times N}\) : User-Item Interaction Matrix
  • \(\mathbf{P}_{\text{RL}}=\text{MLP}_{\text{ReLU}}\left(\mathbf{R}\right) \in \mathbb{R}^{M \times K}\) : User-Latent Factor Matrix of Representation Learning
  • \(\mathbf{Q}_{\text{RL}}=\text{MLP}_{\text{ReLU}}\left(\mathbf{R}^{T}\right) \in \mathbb{R}^{N \times K}\) : Item-Latent Factor Matrix of Representation Learning
  • \(\mathbf{Y}_{\text{RL}} \in \mathbb{R}^{(M \times N) \times K}\) : Predictive Vector of Representation Learning

• Matching Function Learning : Linear Transformation

  \[\begin{aligned} \mathbf{Y}_{\text{ML}} &= \text{MLP}_{\text{ReLU}}\left[\mathbf{P}_{\text{ML}} \oplus \mathbf{Q}_{\text{ML}}\right] \end{aligned}\]
  • \(\mathbf{P}_{\text{ML}} = \mathbf{W}^{(P)} \cdot \mathbf{R} \in \mathbb{R}^{M \times K}\) : User-Latent Factor Matrix of Matching Function Learning
  • \(\mathbf{Q}_{\text{ML}} = \mathbf{W}^{(Q)} \cdot \mathbf{R}^{T} \in \mathbb{R}^{N \times K}\) : Item-Latent Factor Matrix of Matching Function Learning
  • \(\mathbf{Y}_{\text{RL}} \in \mathbb{R}^{(M \times N) \times K}\) : Predictive Vector of Matching Function Learning

• Fusion

  \[\begin{aligned} \mathbf{Y} &= \sigma\left[\mathbf{Y}_{\text{RL}} \oplus \mathbf{Y}_{\text{ML}}\right] \end{aligned}\]

Dual Embedding Method: DNCF

---

• DELF(Dual-Embedding based Latent Factor Model)
  • ID Embedding : 사용자, 아이템의 ID만을 활용하므로 사용자 행동 패턴이나 아이템 구매 패턴을 유추할 만한 맥락 정보가 부족함
  • History Embedding : 사용자와 아이템의 고유한 정체성, 예컨대 사용자의 독립적인 선호나 아이템의 독립적 특성보다는 과거 어떤 아이템, 사용자와 상호작용했는지에 지나치게 의존함
  • 이중 임베딩(Dual-Embedding)을 결합하지 않고 독립적으로 학습하여 최종 표현을 생성하므로 각각의 한계점을 서로 보완하는 표현력을 기대하기 어려움
• DNCF(Dual-embedding based Neural Collaborative Filtering) : 이중 임베딩을 사용하되, 두 임베딩을 결합하여 학습함으로써 사용자, 아이템 표현을 개선함
  • Dual-embedding based Neural Collaborative Filtering for Recommender Systems(2021)

How to Modeling

• ID based Embedding

  \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u}&=\text{Embedding}\left[\overrightarrow{\mathbf{z}}_{u}\right] \in \mathbb{R}^{K}\\ \overrightarrow{\mathbf{q}}_{i}&=\text{Embedding}\left[\overrightarrow{\mathbf{z}}_{i}\right] \in \mathbb{R}^{K} \end{aligned}\]
  • $\overrightarrow{\mathbf{z}}_{u}$ : ID One-Hot Vector of User $i$
  • $\overrightarrow{\mathbf{z}}_{i}$ : ID One-Hot Vector of Item $j$
  • $\overrightarrow{\mathbf{p}}_{u}$ : ID Embedding Vector of User $i$
  • $\overrightarrow{\mathbf{q}}_{i}$ : ID Embedding Vector of Item $j$

• Interaction based Embedding

  \[\begin{aligned} \overrightarrow{\mathbf{m}}_{u} &=\text{AGG}\left[\left\{\overrightarrow{\mathbf{h}}_{j} \mid j \in \mathcal{R}_{u}^{+}\right\}\right] \in \mathbb{R}^{K}\\ &=\frac{1}{\sqrt{\vert \mathcal{R}_{u}^{+}\vert}}\mathbf{W}^{(P)} \cdot \mathbf{R}_{u,:}\\ \overrightarrow{\mathbf{n}}_{i} &=\text{AGG}\left[\left\{\overrightarrow{\mathbf{h}}_{v} \mid v \in \mathcal{R}_{i}^{+}\right\}\right] \in \mathbb{R}^{K}\\ &=\frac{1}{\sqrt{\vert \mathcal{R}_{i}^{+}\vert}}\mathbf{W}^{(Q)} \cdot \mathbf{R}_{:,i} \end{aligned}\]
  • $\mathbf{R}_{u,:}$ : Multi-Hot Vector of User $u$ @ User-Item Interaction Matrix
  • $\mathbf{R}_{:,i}$ : Multi-Hot Vector of Item $i$ @ User-Item Interaction Matrix
  • $\overrightarrow{\mathbf{m}}_{u}$ : ID Embedding Vector of User $u$
  • $\overrightarrow{\mathbf{n}}_{i}$ : ID Embedding Vector of Item $i$
• Embedding Combination

  • User Embedding Combination:

    \[\begin{aligned} \overrightarrow{\mathbf{x}}_{u} &=\overrightarrow{\mathbf{p}}_{u} \oplus \overrightarrow{\mathbf{m}}_{u} \in \mathbb{R}^{2K} \end{aligned}\]

  • Item Embedding Combination:

    \[\begin{aligned} \overrightarrow{\mathbf{y}}_{i} &=\overrightarrow{\mathbf{q}}_{i} \oplus \overrightarrow{\mathbf{n}}_{i} \in \mathbb{R}^{2K} \end{aligned}\]

• Neural Collaborative Filtering and Predict

  \[\begin{aligned} \hat{r}_{u,i} &= \sigma\Big[\text{MLP}_{\text{ReLU}}\left[\overrightarrow{\mathbf{x}}_{u} \oplus \overrightarrow{\mathbf{y}}_{i}\right]\Big] \end{aligned}\]

Semi-Dual Embedding Method: DRNet

---

• Previous Research
  • User based Collaborative Filtering : 선호 패턴이 유사한 사용자 간 연관성을 학습할 수 있지만, 아이템 특성을 명시적으로 표현할 수 없음
  • Item based Collaborative Filtering : 구매 패턴이 유사한 아이템 간 연관성을 학습할 수 있지만, 사용자 선호를 명시적으로 표현할 수 없음
  • Latent Factor Model : 사용자와 아이템의 고유성을 명시적으로 표현할 수 있지만, 희박성(Sparsity)이 높을 경우 표현력을 신뢰할 수 없고, 특정 아이템과 사용자의 과거 행동 간 연관성을 반영하지 못함
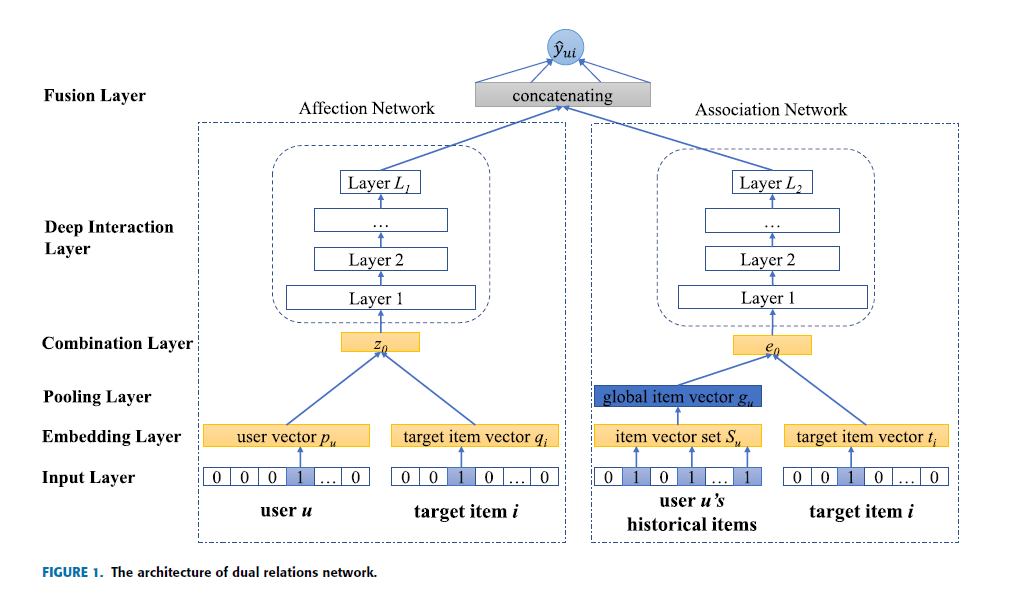
• DRNet(Dual Relation Net-work) : Latent Factor Model 과 Item based Collaborative Filtering 을 결합하여 사용자-아이템 관계와 아이템-아이템 관계를 동시에 모델링함으로써 개인화 추천 정확도를 높이면서도 데이터 희박성 문제에 대한 강건성을 도모함
  • Dual Relations Network for Collaborative Filtering(2020)

How to Modeling

• Affection Network : Modeling User-Item Relation

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i}^{\text{Affection}} &= \text{MLP}_{\text{ReLU}}\left[\overrightarrow{\mathbf{p}}_{u} \odot \overrightarrow{\mathbf{q}}_{i}\right] \end{aligned}\]

• Association Network : Modeling Item-Item Relation

  • Global Item Vector of User $u$:

    \[\begin{aligned} \overrightarrow{\mathbf{g}}_{u} &= \text{ATTN}\left[\overrightarrow{\mathbf{v}}_{i}, \overrightarrow{\mathbf{s}}^{(u)}_{j}, \overrightarrow{\mathbf{s}}^{(u)}_{j}\right] \in \mathbb{R}^{K} \end{aligned}\]
    • $i$ : Target Item
    • $j^{\forall} \in \mathbf{R}_{u}^{+} \setminus i$ : Interaction Item of User $u$
    • $\overrightarrow{\mathbf{v}}_{i} \in \mathbb{R}^{K}$ : Target Item Vector @ Association Network
    • $\overrightarrow{\mathbf{s}}^{(u)}_{j} \in \mathbb{R}^{K}$ : Historical Item Vector of User $u$

  • Deep Interaction:

    \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u,i}^{\text{Association}} &= \text{MLP}_{\text{ReLU}}\left[\overrightarrow{\mathbf{g}}_{u} \odot \overrightarrow{\mathbf{v}}_{i}\right] \end{aligned}\]

• Fusion

  \[\begin{aligned} r_{u,i} &= \sigma\left[\overrightarrow{\mathbf{z}}_{u,i}^{\text{Affection}} \oplus \overrightarrow{\mathbf{z}}_{u,i}^{\text{Association}} \right] \end{aligned}\]

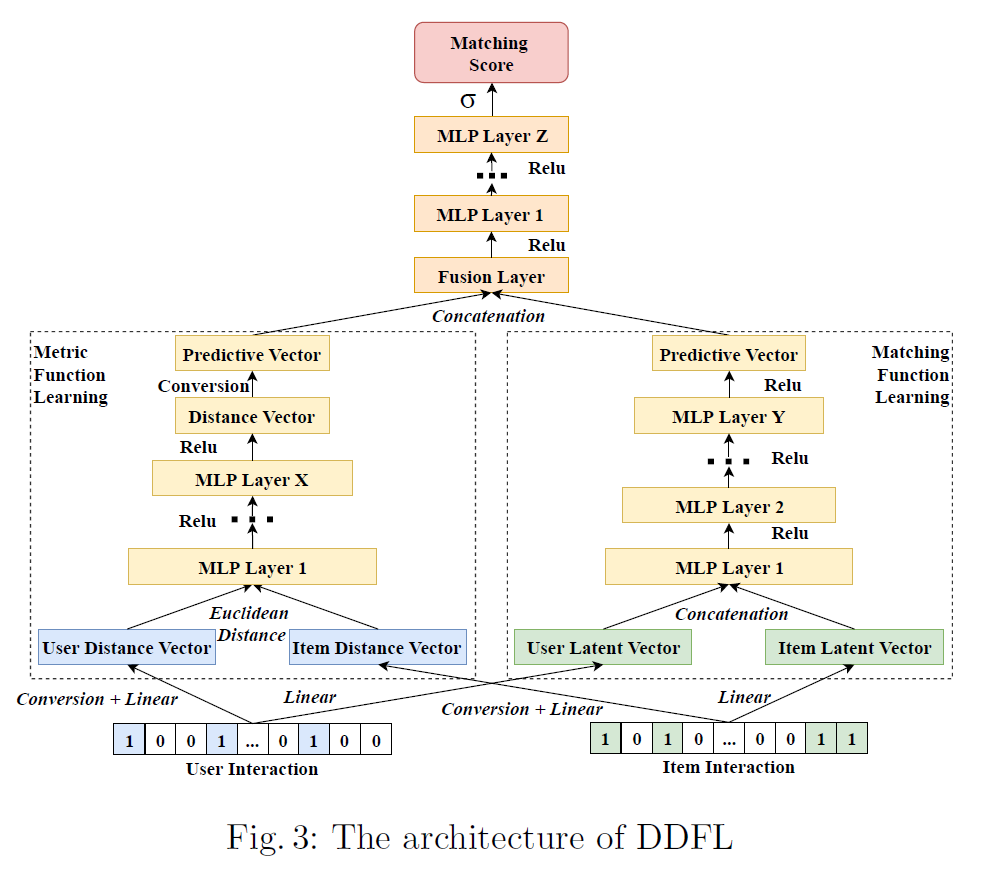
Distance Embedding Method: DDFL

---

• Representation Learning based Collaborative Filtering : 내적(Dot Product)을 활용한 유사도 계산은 삼각 부등식(Triangular Inequality)을 만족하지 못함

  • 삼각 부등식(Triangular Inequality) : 세 점 사이의 거리에 대한 제한 조건으로서, $A$ 와 $C$ 사이 거리는 $A$ 에서 $B$, 그리고 $B$ 에서 $C$ 로 우회하는 거리보다 크거나 같아야 함

    \[\begin{aligned} \text{d}\left[A,C\right] \le \text{d}\left[A,B\right] + \text{d}\left[B,C\right] \end{aligned}\]

  • 즉, 사용자 $u$ 가 아이템 $i$ 를 직접적으로 선호하는 정도는, 사용자 $u$ 가 아이템 $j$ 를 선호하는 정도 및 아이템 $i$ 와 $j$ 간 유사한 정도의 합보다 작거나 같아야 함

    \[\begin{aligned} \overrightarrow{\mathbf{p}}_{u} \cdot \overrightarrow{\mathbf{q}}_{i} \le \overrightarrow{\mathbf{p}}_{u} \cdot \overrightarrow{\mathbf{q}}_{j} + \overrightarrow{\mathbf{q}}_{i} \cdot \overrightarrow{\mathbf{q}}_{j} \end{aligned}\]
• DDFL(Deep Dual Function Learning-based Model) : 히스토리 임베딩(History Embedding)에서 표현 학습과 매칭 함수 학습을 결합하는 대신, 거리 함수 학습(MeFL)과 매칭 함수 학습(MaFL)을 결합함으로써 삼각 부등식이 위배됨에 따른 비합리적 추천 결과를 보완함
  • DDFL: A Deep Dual Function Learning-Based Model for Recommender Systems(2020)

How to Modeling

• MeFL(Metric Function Learning) : 사용자, 아이템 표현 학습 시 삼각 부등식을 고려함으로써 합리적 추천 결과를 도모함

  • Conversion Transformation:

    \[\begin{aligned} y_{u,i}&=\alpha\left(1-r_{u,i}\right) \end{aligned}\]
    • $r_{u,i} \in \mathbf{R}$ is Implicit Feedback

  • Linear Transformation:

    \[\begin{aligned} \mathbf{P}^{\text{MeFL}}&= \mathbf{W}_{\text{MeFL}}^{(P)} \cdot \mathbf{Y} \in \mathbb{R}^{M \times K}\\ \mathbf{Q}^{\text{MeFL}}&= \mathbf{W}_{\text{MeFL}}^{(P)} \cdot \mathbf{Y}^{T} \in \mathbb{R}^{N \times K} \end{aligned}\]

  • Calculate Euclidean Distance:

    \[\begin{aligned} \overrightarrow{\mathbf{d}}_{u,i} = \begin{bmatrix} \left(p^{\text{MeFL}}_{u,1}-q^{\text{MeFL}}_{i,1}\right)^{2} & \left(p^{\text{MeFL}}_{u,2}-q^{\text{MeFL}}_{i,2}\right)^{2} & \cdots & \left(p^{\text{MeFL}}_{u,K}-q^{\text{MeFL}}_{i,K}\right)^{2} \end{bmatrix} \end{aligned}\]

  • Metric Function Predictive Vector:

    \[\begin{aligned} \overrightarrow{\mathbf{z}}^{\text{MeFL}}_{u,i} &= \text{MLP}_{\text{ReLU}}\left[\overrightarrow{\mathbf{d}}_{u,i}\right] \end{aligned}\]

• MaFL(Matching Function Learning)

  • Linear Transformation:

    \[\begin{aligned} \mathbf{P}^{\text{MaFL}}&= \mathbf{W}_{\text{MaFL}}^{(P)} \cdot \mathbf{R} \in \mathbb{R}^{M \times K}\\ \mathbf{Q}^{\text{MaFL}}&= \mathbf{W}_{\text{MaFL}}^{(Q)} \cdot \mathbf{R}^{T} \in \mathbb{R}^{N \times K} \end{aligned}\]

  • Matching Function Predictive Vector:

    \[\begin{aligned} \overrightarrow{\mathbf{z}}^{\text{MaFL}}_{u,i} &= \text{MLP}_{\text{ReLU}}\left[\overrightarrow{\mathbf{p}}_{u} \oplus \overrightarrow{\mathbf{q}}_{i}\right] \end{aligned}\]

• Fusion

  \[\begin{aligned} \hat{r}_{u,i} &= \sigma\Bigg(\text{MLP}_{\text{ReLU}}\left[\overrightarrow{\mathbf{z}}^{\text{MeFL}}_{u,i} \oplus \overrightarrow{\mathbf{z}}^{\text{MaFL}}_{u,i}\right]\Bigg) \end{aligned}\]