Optimizer
Based on the lecture “Intro. to Deep Learning (2023-2)” by Prof. Seong Man An, Dept. of Data Science, The Grad. School, Kookmin Univ.
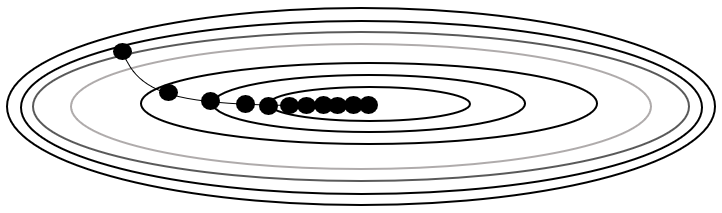
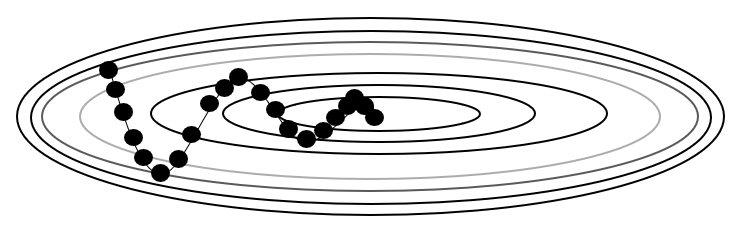
Gradient Descent
-
그라디언트(Gradient) : 다변수 함수에 대하여 모든 방향으로의 순간변화율 벡터
\[\begin{aligned} \nabla{f(x_{1},x_{2},\cdots,x_{n})} &= \begin{pmatrix} \displaystyle\frac{\partial f(x^{\forall})}{\partial x_{1}}\\ \displaystyle\frac{\partial f(x^{\forall})}{\partial x_{2}}\\ \vdots\\ \displaystyle\frac{\partial f(x^{\forall})}{\partial x_{n}}\\ \end{pmatrix} \end{aligned}\] -
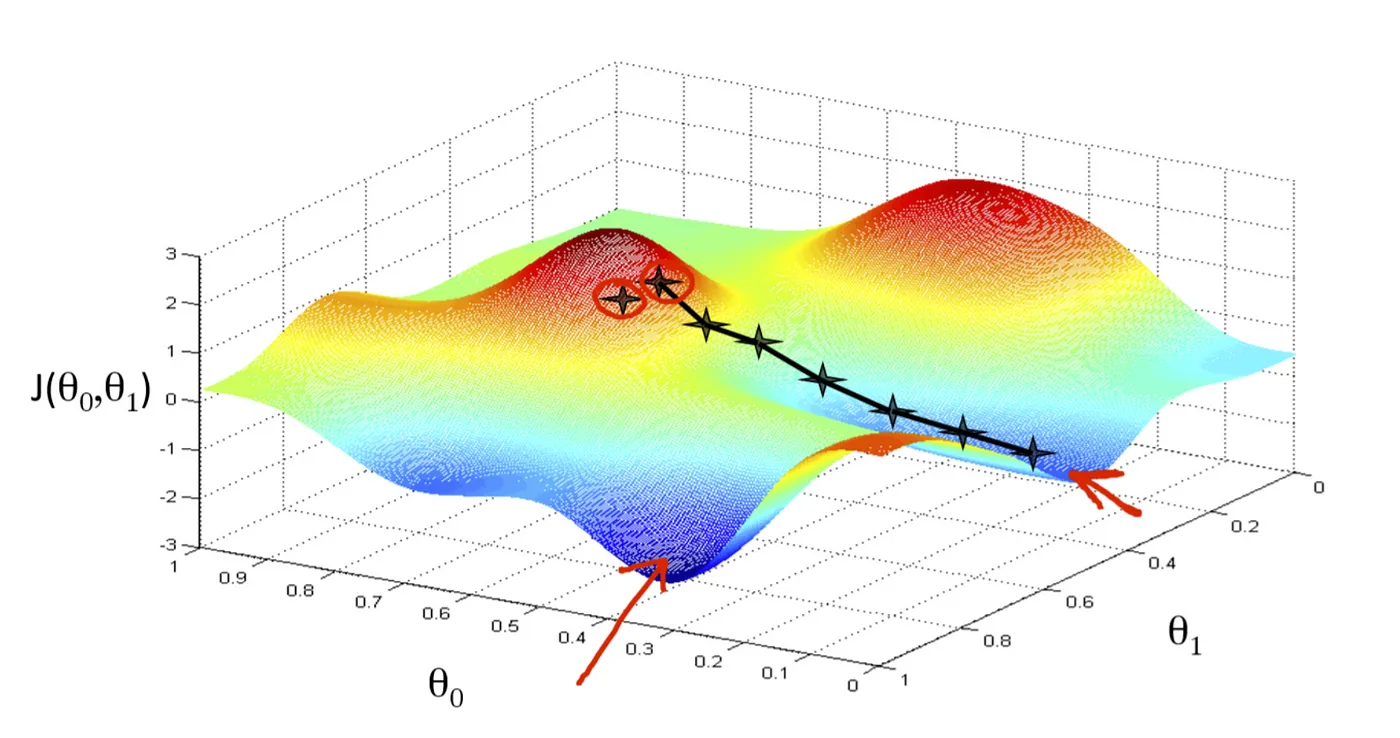
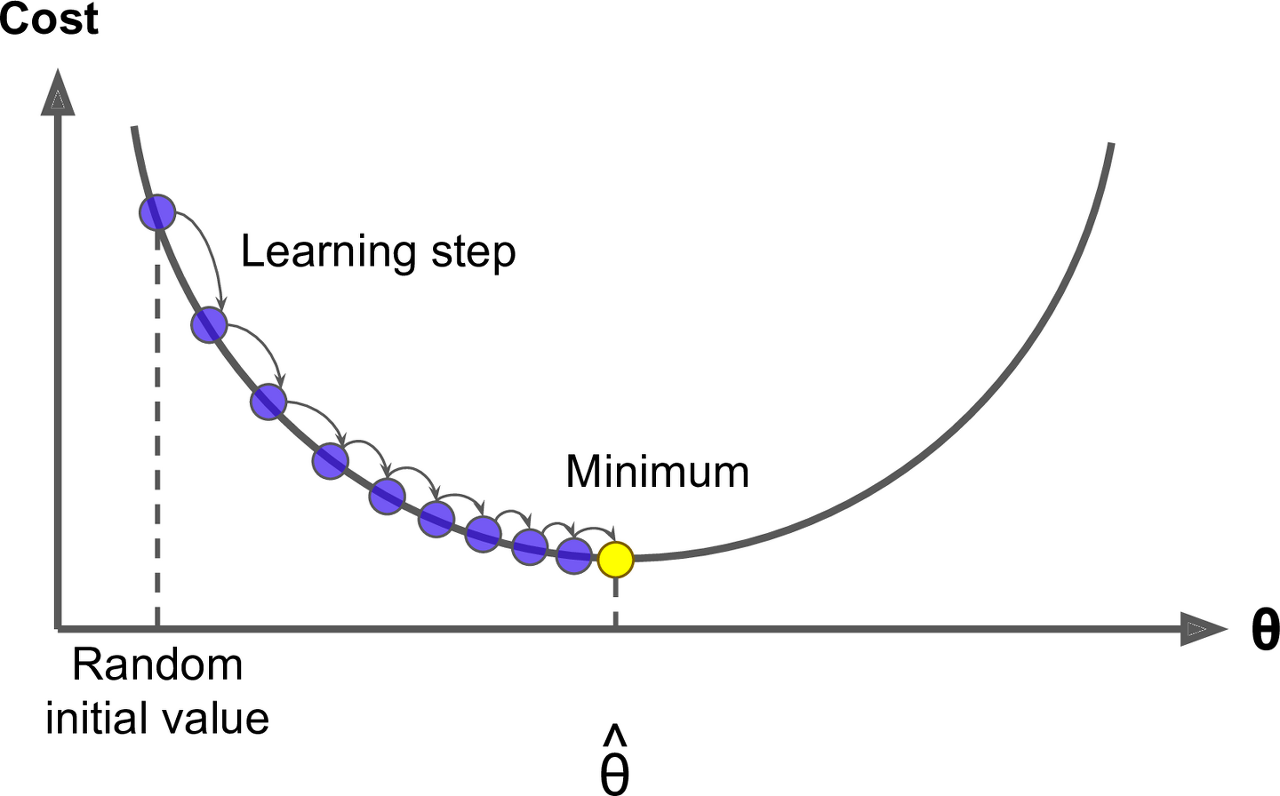
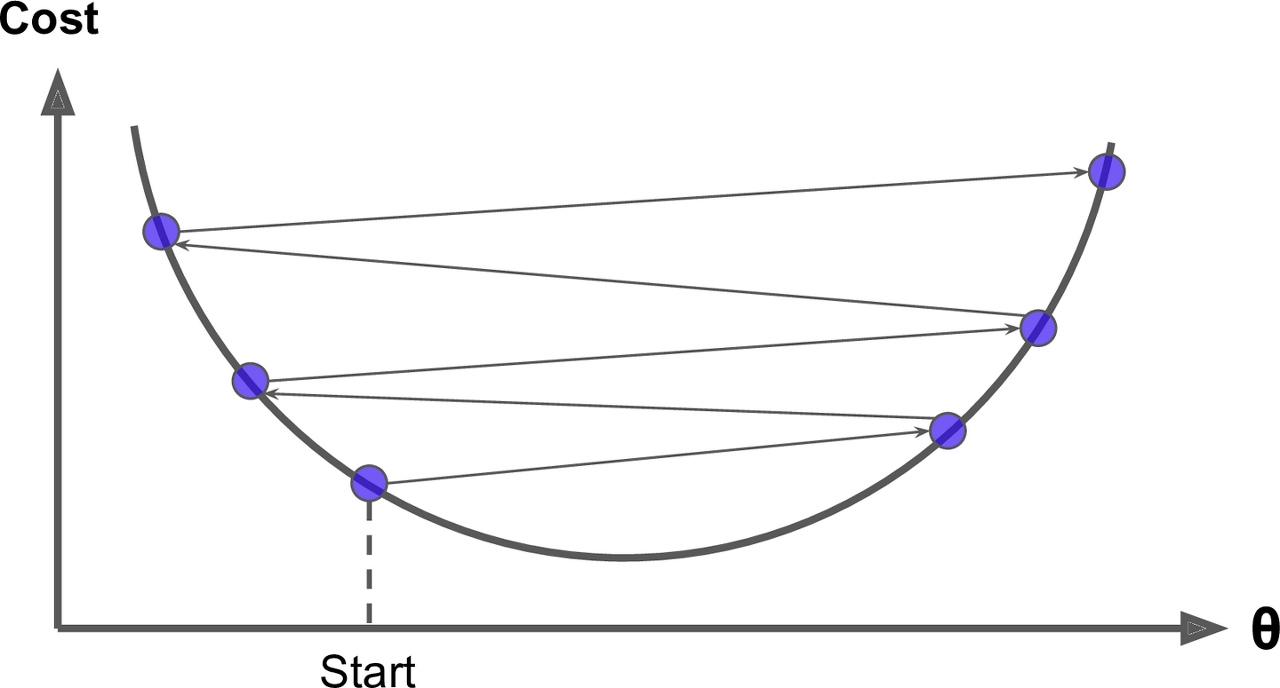
경사하강법(Gradient Descent) : 손실 함수의 도함수(그라디언트)를 최소화하는 가중치를 추정하는 방법
-
절차
- 파라미터 $\overrightarrow{w}$ 의 초기 아규먼트 설정
- 현재 아규먼트 \(\overrightarrow{w}_{prev}\) 에서 손실 함수의 그라디언트 \(\nabla{Loss(\overrightarrow{w}_{prev})}\) 계산
- 현재의 아규먼트에서 음의 방향으로 \(\alpha \times \nabla{Loss(\overrightarrow{w}_{prev})}\) 만큼 이동하여 새로운 아규먼트 \(\overrightarrow{w}_{new}\) 적용
- ②, ③을 반복하여 손실 함수를 최소화하는 지점 탐색
-
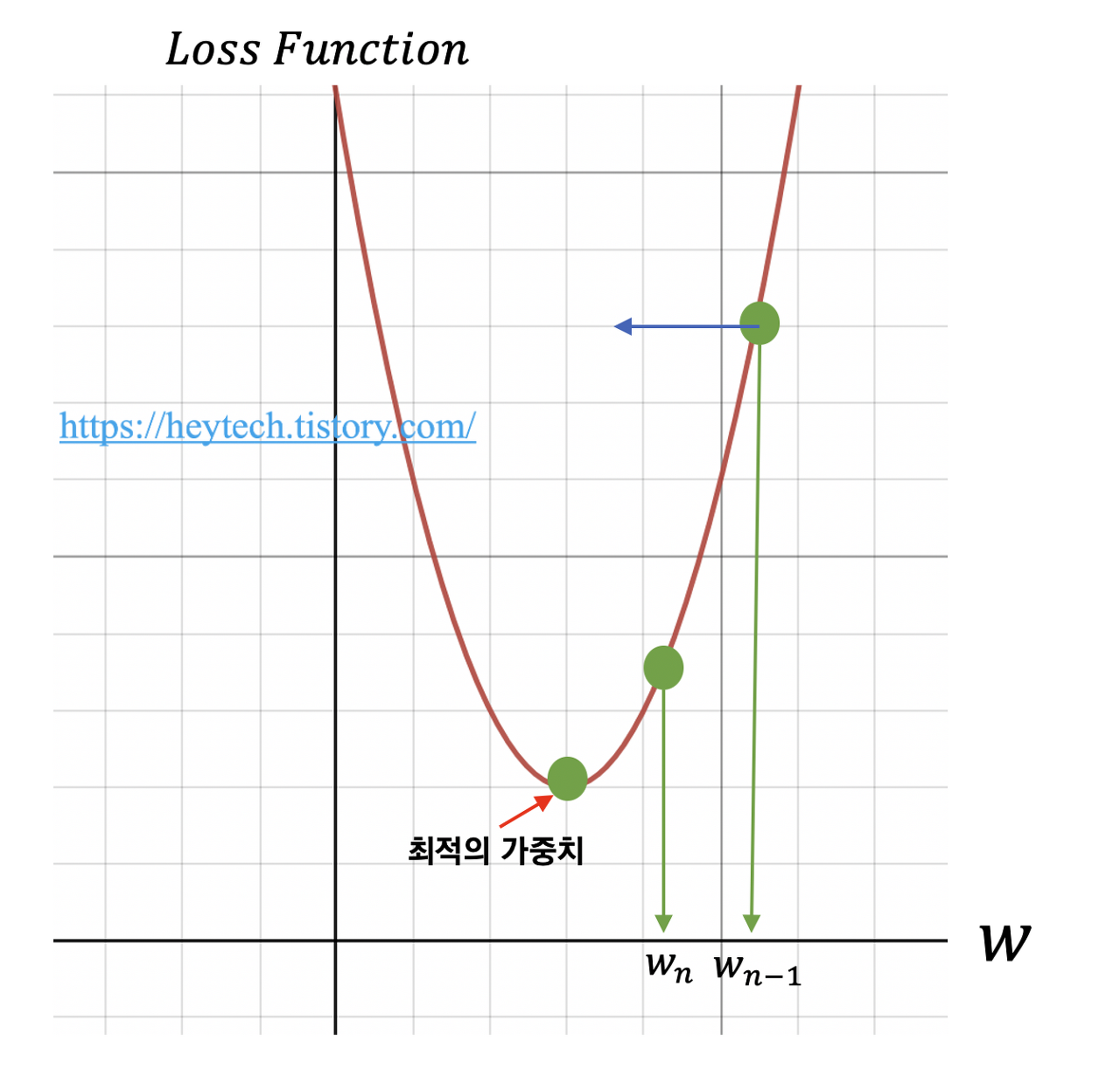
아규먼트 갱신 규칙
\[\begin{aligned} \overrightarrow{w}_{new} &= \overrightarrow{w}_{prev} - \alpha \times \nabla{Loss(\overrightarrow{w}_{prev})} \end{aligned}\] -
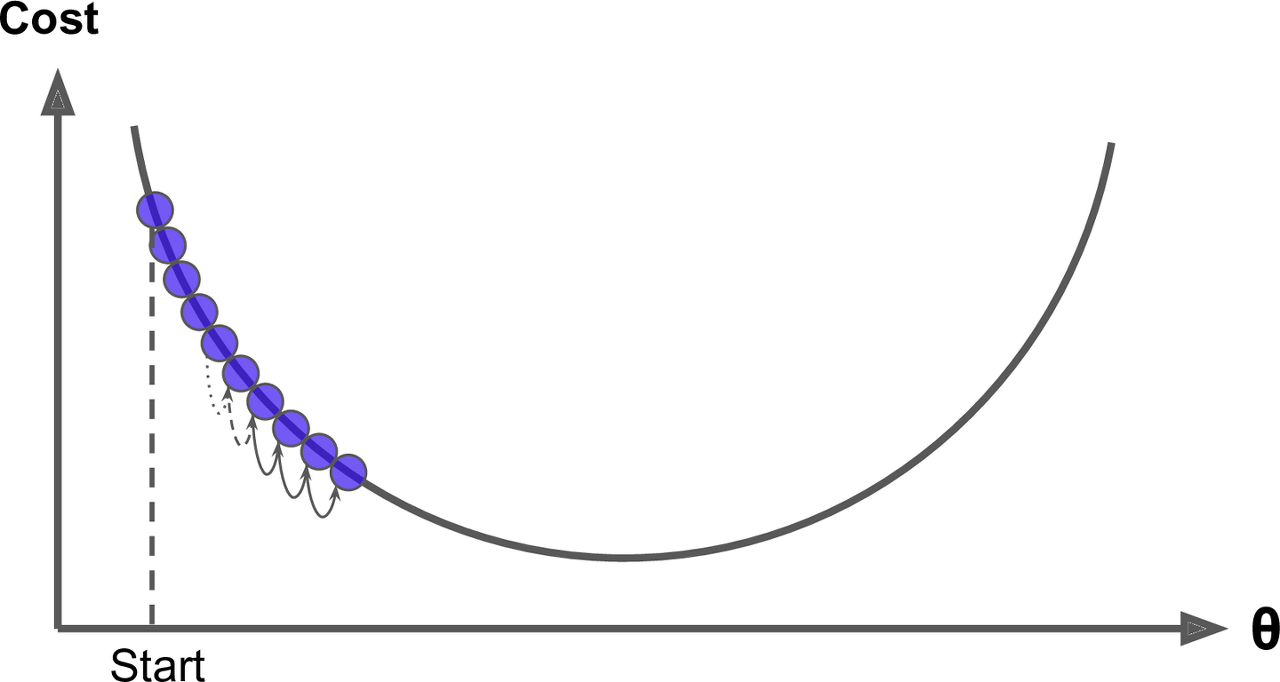
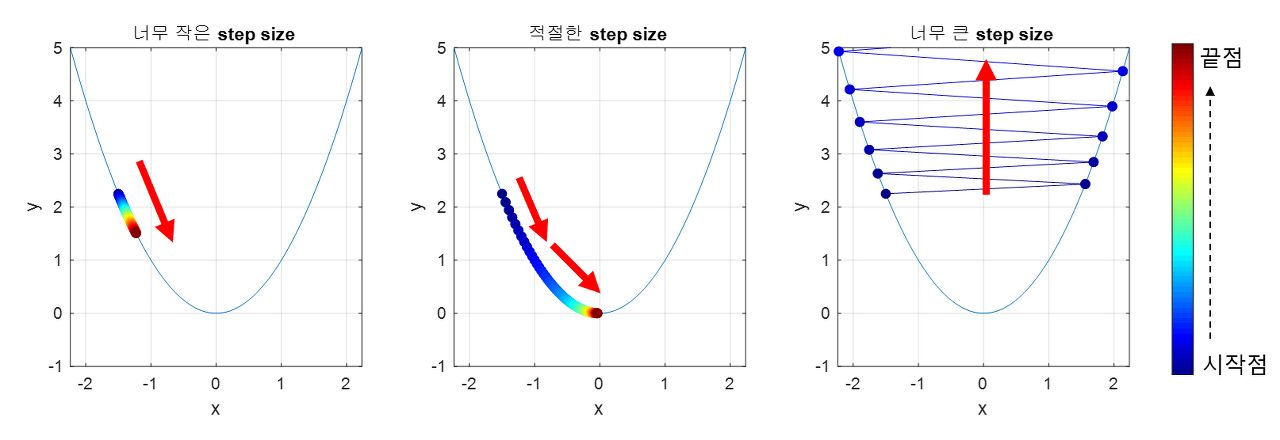
학습률(Learning Rate) : 손실 함수에 대하여 그 극소점을 탐색하기 위한 아규먼트 갱신 보폭
Example: three-layer model
Forward Propagation Process
-
손실 $e$ 를 다음과 같이 정의하자
\[\begin{aligned} e &= \text{Loss}(\hat{y})\\ &= \hat{y} - y \end{aligned}\]- $\hat{y}$ : 예측값
- $y$ : 실제값
-
$n$ 개의 계층으로 구성된 모델의 예측값 $\hat{y}$ 은 다음과 같음
\[\hat{y} = f_{n} \circ g_{n} \circ f_{n-1} \circ g_{n-1} \circ \cdots \circ f_{1} \circ g_{1}(x)\]-
$x$ : 입력값
-
$f_{i}(x)$ : $i$ 번째 계층의 활성화 함수
-
$g_{i}(x)=w_{i} \cdot x + b_{i}$ : $i$ 번째 계층의 순입력 함수
- $w_{i}$ : $i$ 번째 계층의 가중치
- $b_{i}$ : $i$ 번째 계층의 편향으로서 편의상 $0$ 이라고 가정함
-
-
$3$ 개의 계층으로 구성된 모델의 손실 $e$ 를 다음과 같이 서술할 수 있음
\[\begin{aligned} e &= h_{3} - y\\ &= f_{3}(z_{3}) - y\\ &= f_{3}(g_{3}(h_{2})) - y\\ &= f_{3}(w_{3} \cdot h_{2}) - y\\ &= f_{3}(w_{3} \cdot f_{2}(z_{2})) - y\\ &= f_{3}(w_{3} \cdot f_{2}(g_{2}(h_{1}))) - y\\ &= f_{3}(w_{3} \cdot f_{2}(w_{2} \cdot h_{1})) - y\\ &= f_{3}(w_{3} \cdot f_{2}(w_{2} \cdot f_{1}(z_{1}))) - y\\ &= f_{3}(w_{3} \cdot f_{2}(w_{2} \cdot f_{1}(g_{1}(h_{0})))) - y\\ &= f_{3}(w_{3} \cdot f_{2}(w_{2} \cdot f_{1}(w_{1} \cdot h_{0}))) - y \end{aligned}\]- $z_{i}=g_{i}(h_{i-1})$ : $i$ 번째 계층의 순입력 함수 값
- $h_{i}=f_{i}(z_{i})$ : $i$ 번째 계층의 활성화 함수 값
- $h_{0} = x$ : 입력값
Backward Propagation Process
-
손실 $e$ 를 $1$ 번째 계층 가중치 $w_{1}$ 에 대하여 미분하면 다음과 같음
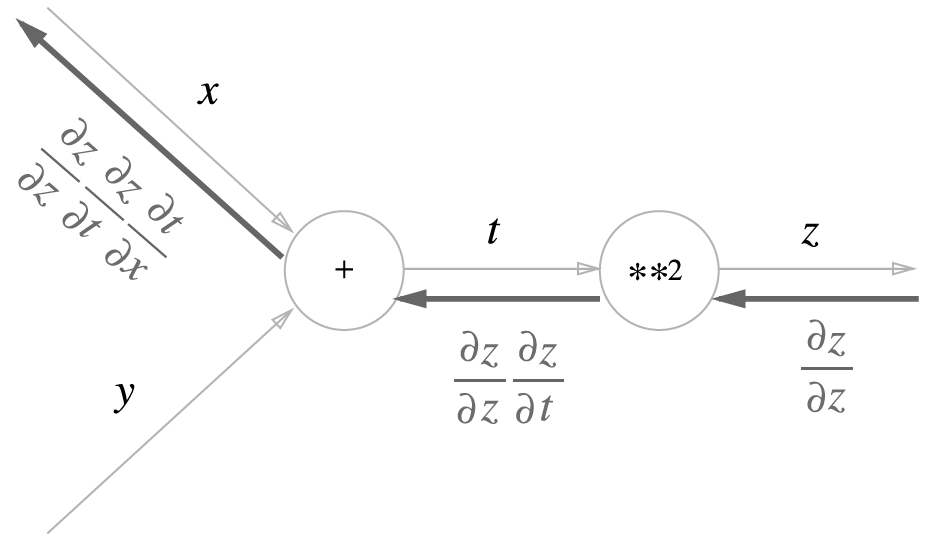
\[\begin{aligned} \frac{\partial e}{\partial w_{1}} &= \frac{\partial e}{\partial\not{h_{3}}} \cdot \frac{\partial\not{h_{3}}}{\partial\not{z_{3}}} \cdot \frac{\partial\not{z_{3}}}{\partial\not{h_{2}}} \cdot \frac{\partial\not{h_{2}}}{\partial\not{z_{2}}} \cdot \frac{\partial\not{z_{2}}}{\partial\not{h_{1}}} \cdot \frac{\partial\not{h_{1}}}{\partial\not{z_{1}}} \cdot \frac{\partial\not{z_{1}}}{\partial w_{1}} \end{aligned}\] -
위 수식의 각 항목을 다음과 같이 일반화할 수 있음
\[\begin{aligned} \frac{\partial e}{\partial h_{n}} &= \frac{\partial(h_{n}-y)}{\partial h_{n}}\\ &= 1\\\\ \frac{\partial h_{i}}{\partial z_{i}} &= \frac{\partial f_{i}(z_{i})}{\partial z_{i}}\\ &= f^{\prime}_{i}(z_{i})\\\\ \frac{\partial z_{i}}{\partial h_{i-1}} &= \frac{\partial g_{i}(h_{i-1})}{\partial h_{i-1}}\\ &= \frac{\partial (w_{i} \cdot h_{i-1})}{\partial h_{i-1}}\\ &= w_{i}\\\\ \frac{\partial z_{i}}{\partial w_{i}} &= \frac{\partial g_{i}(h_{i-1})}{\partial w_{i}}\\ &= \frac{\partial (w_{i} \cdot h_{i-1})}{\partial w_{i}}\\ &= h_{i-1} \end{aligned}\] -
손실 $e$ 를 $k$ 번째 계층 가중치 $w_{k}$ 에 대하여 미분한 값을 다음과 같이 일반화할 수 있음
\[\begin{aligned} \frac{\partial e}{\partial w_{k}} &= h_{k-1} \times (w_{n} \cdot w_{n-1} \cdots w_{k+1}) \times \{f^{\prime}_{n}(z_{n}) \cdot f^{\prime}_{n-1}(z_{n-1}) \cdots f^{\prime}_{k}(z_{k})\}\\ &= h_{k-1} \times \displaystyle\prod^{n}_{i=k+1}{w_i} \times \displaystyle\prod^{n}_{i=k}{f^{\prime}_{i}(z_{i})} \end{aligned}\]- $h_{k-1}$ : $k-1$ 번째 계층 출력값이자 $k$ 번째 계층 입력값
- $\displaystyle\prod^{n}_{i=k+1}{w_i}$ : 출력층에서부터 $k+1$ 번째 계층까지 가중치 곱
- \(\displaystyle\prod^{n}_{i=k}{f^{\prime}_{i}(z_{i})}\) : 출력층에서부터 $k$ 번째 계층까지 활성화 함수 값 곱
-
경사하강법에 의해 갱신된 $k$ 번째 계층의 가중치 $(w_{k})_{new}$ 는 다음과 같음
\[\begin{aligned} (w_{k})_{new} &= w_{k} - \eta \times \frac{\partial e}{\partial w_{k}}\\ &= w_{k} - \eta \times h_{k-1} \displaystyle\prod^{n}_{i=k+1}{w_i} \cdot \displaystyle\prod^{n}_{i=k}{f^{\prime}_{i}(z_{i})} \end{aligned}\]
Type
경사하강법 각 항목의 의미
\[w_{t} =w_{t-1} - \eta \times \frac{\partial e_{t-1}}{\partial w_{t-1}}\]-
$\eta$ : 학습률(Learning Rate)로서 갱신 크기
-
$\displaystyle\frac{\partial e_{t-1}}{\partial w_{t-1}}$ : 가중치에 대한 손실의 변화율 벡터로서 갱신 방향
갱신 크기 중심
-
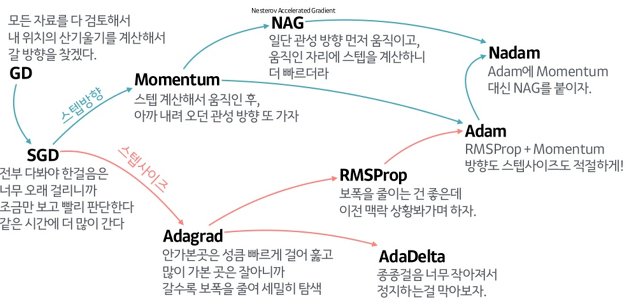
\[\begin{aligned} w_{t} &= w_{t-1} - \frac{\eta}{\sqrt{h_{t}}} \times \frac{\partial e_{t-1}}{\partial w_{t-1}}\\ h_{t} &= h_{t-1} + \frac{\partial e_{t}}{\partial w_{t}} \odot \frac{\partial e_{t}}{\partial w_{t}} \end{aligned}\]Adagrad: 갱신 크기를 결정함에 있어 이전까지 갱신 규모를 반영함-
$h_{t-1}$ : 이전까지 갱신 규모
-
$\displaystyle\frac{\partial e_{t}}{\partial w_{t}} \odot \displaystyle\frac{\partial e_{t}}{\partial w_{t}}$ : 현 시점 갱신 규모 추정치
-
-
\[\begin{aligned} w_{t} &= w_{t-1} - \frac{\eta}{\sqrt{h_{t}}} \times \frac{\partial e_{t-1}}{\partial w_{t-1}}\\ h_{t} &= \rho \cdot h_{t-1} + (1 - \rho) \cdot \frac{\partial e_{t}}{\partial w_{t}} \odot \frac{\partial e_{t}}{\partial w_{t}} \end{aligned}\]RMSProp: 갱신 크기를 결정함에 있어 이전까지 갱신 규모를 지수가중이동평균하여 반영함- $\rho$ : 붕괴 계수
갱신 방향 중심
-
\[\begin{aligned} w_{t} &= w_{t-1} - m_{t}\\ m_{t} &= \eta \cdot \frac{\partial e_{t-1}}{\partial w_{t-1}} + \gamma \cdot m_{t-1} \end{aligned}\]Momentum: 갱신 방향을 결정함에 있어 $m_{t-1}$ 을 $\gamma$ 만큼 반영함- $m_{t-1}$ : 직전 시점 갱신 방향
- $\gamma$ : 관성 계수
이미지 출처
- https://towardsdatascience.com/an-intuitive-explanation-of-gradient-descent-83adf68c9c33