Principal Component Analysis

Prerequisite

---

Projection

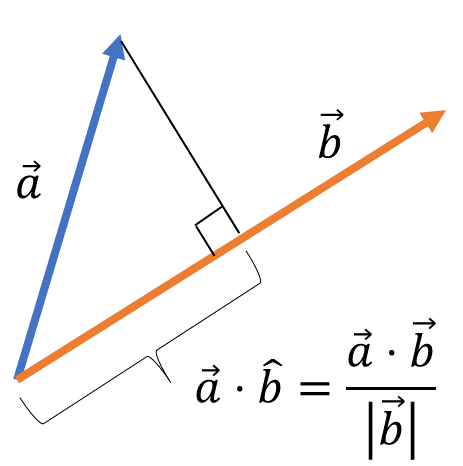
• 벡터 $\overrightarrow{a}$ 를 벡터 $\overrightarrow{b}$ 에 정사영했을 때, 정사영 벡터 $\text{proj}_{\overrightarrow{b}}(\overrightarrow{a})$ 는 다음과 같음

  \[\begin{aligned} \cos{90^{\circ}} &= \frac{(\overrightarrow{a}-p\overrightarrow{b})^{T}\overrightarrow{b}}{\Vert \overrightarrow{a}\Vert \cdot \Vert\overrightarrow{b}\Vert}\\ &= 0\\ \therefore \text{proj}_{\overrightarrow{b}}(\overrightarrow{a}) &= p\overrightarrow{b}\\ &= \left(\frac{\overrightarrow{a}^{T}\overrightarrow{b}}{\Vert\overrightarrow{b}\Vert^{2}}\right)\overrightarrow{b} \end{aligned}\]
  • $p=\displaystyle\frac{\overrightarrow{a}^{T}\overrightarrow{b}}{\Vert\overrightarrow{b}\Vert^{2}}$ : 정사영 벡터의 크기
  • $\overrightarrow{b}$ : 정사영 벡터의 방향

Covariance Matrix

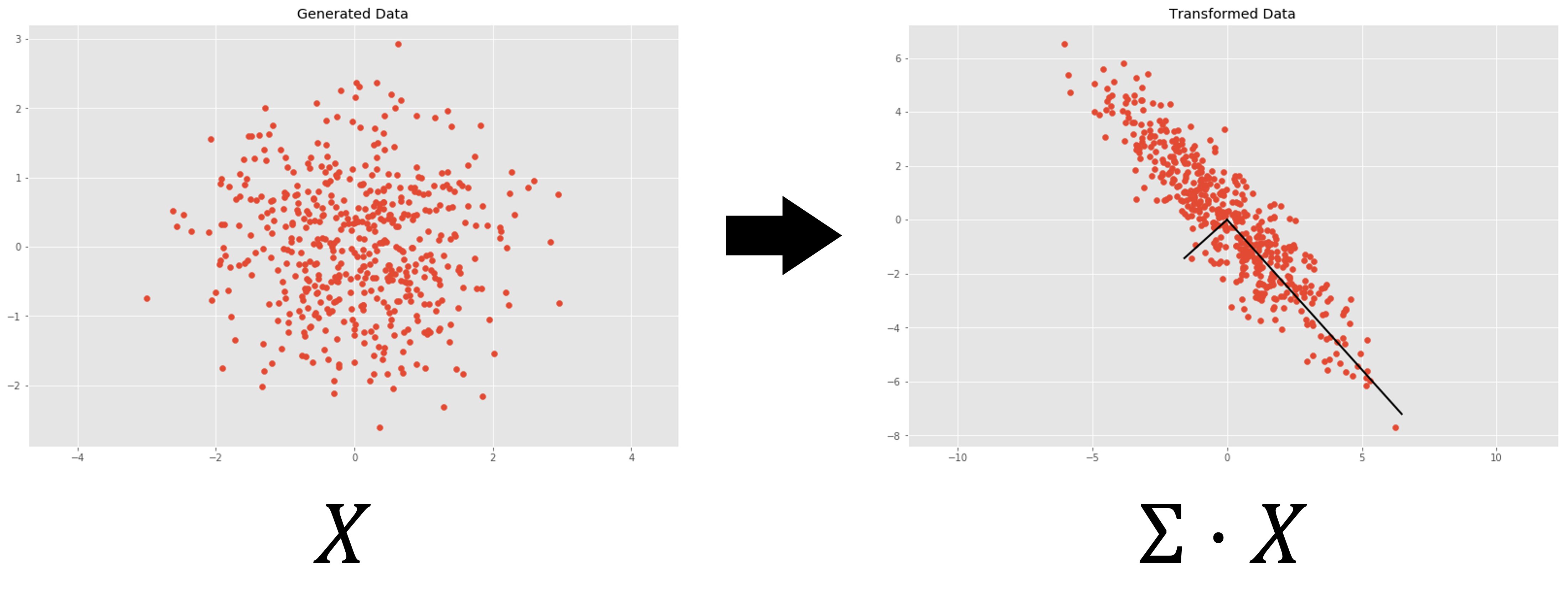
• 공분산(Covariance) : 두 확률변수의 선형관계를 나타내는 지표로서, 두 확률변수의 편차(관측치와 평균 사이 거리)를 곱한 값의 평균

  \[\sigma_{XY} = \frac{1}{N}\sum_{i=1}^{N}(X_{i}-\mu_X)(Y_{i}-\mu_Y)\]

• 공분산행렬(Covariance Matrix) : $n$ 개 변수들 간 공분산을 나열한 $n \times n$ 정방행렬

  \[\Sigma= \begin{matrix} & \overrightarrow{A} & \overrightarrow{B} & \overrightarrow{C} \\ \overrightarrow{A} & \sigma_{A}^2 & \sigma_{AB} & \sigma_{AC} \\ \overrightarrow{B} & \sigma_{BA} & \sigma_{B}^2 & \sigma_{BC} \\ \overrightarrow{C} & \sigma_{CA} & \sigma_{CB} & \sigma_{C}^2 \end{matrix}\]

Linear Transformation

• 행렬 $\mathbf{X}$ 을 통한 선형변환은 어떤 좌표를 \(\begin{pmatrix}1\\0\end{pmatrix},\begin{pmatrix}0\\1\end{pmatrix}\) 를 기저로 사용하는 2차원 좌표계에서 \(\overrightarrow{x}_{1},\overrightarrow{x}_{2}\) 를 기저로 사용하는 2차원 좌표계로 변환하는 것을 의미함

  \[\begin{aligned} \mathbf{X} &= \begin{pmatrix} 1&3\\-2&0 \end{pmatrix}\\ &= \begin{pmatrix} \overrightarrow{x}_{1}&\overrightarrow{x}_{2} \end{pmatrix} \end{aligned}\]

• 벡터 $\overrightarrow{v}$ 는 \(\begin{pmatrix}1\\0\end{pmatrix},\begin{pmatrix}0\\1\end{pmatrix}\) 를 기저로 사용하는 2차원 좌표계의 좌표 $(-1,2)$ 를 나타냄

  \[\begin{aligned} \overrightarrow{v} &= \begin{pmatrix} 1\\-2 \end{pmatrix}\\ &= -1\begin{pmatrix}1\\0\end{pmatrix} + 2\begin{pmatrix}0\\1\end{pmatrix}\\ \end{aligned}\]

• $\mathbf{X}$ 를 통한 선형 변환 결과 \(\overrightarrow{v}\) 는 \(\overrightarrow{x}_{1},\overrightarrow{x}_{2}\) 를 기저로 사용하는 2차원 좌표계의 좌표 $(-1,2)$ 로 변환되었음

  \[\begin{aligned} \mathbf{X}\cdot\overrightarrow{v} &= \begin{pmatrix} 1&3\\-2&0 \end{pmatrix} \cdot \begin{pmatrix} 1\\-2 \end{pmatrix}\\ &= \begin{pmatrix}-5\\2\end{pmatrix}\\ &= -1\overrightarrow{x}_{1} + 2\overrightarrow{x}_{2} \end{aligned}\]

Eigen-Vector

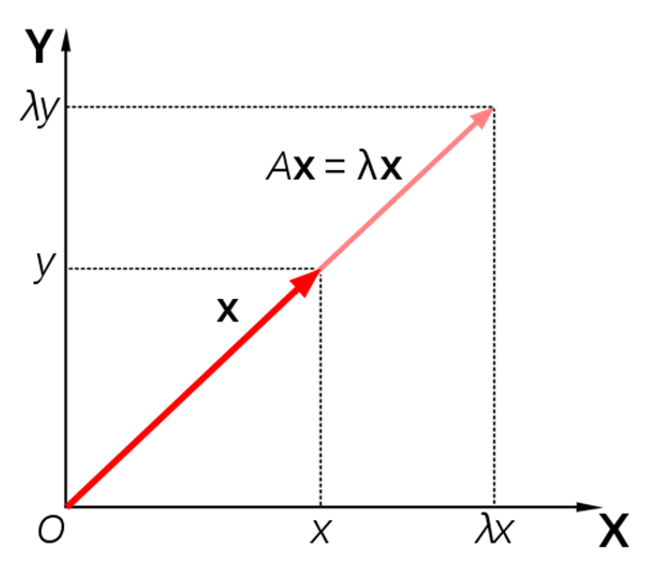
• 고유벡터(Eigen-Vector; $\overrightarrow{v}$) : 정방행렬 $A_n$ 으로 선형변환했을 때, 그 방향은 변하지 않고 단지 크기만 변하는 $\overrightarrow{0}$ 이 아닌 벡터

  \[\begin{aligned} \begin{pmatrix} a_{11}&a_{12}&\cdots&a_{1n}\\ a_{21}&a_{22}&\cdots&a_{1n}\\ \vdots&\vdots&\ddots&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn} \end{pmatrix} \begin{pmatrix} v_{1} \\ v_{2} \\ \vdots \\ v_{n} \end{pmatrix} = \lambda \begin{pmatrix} v_{1} \\ v_{2} \\ \vdots \\ v_{n} \end{pmatrix} \Leftrightarrow A_{n \times n} \overrightarrow{v} = \lambda \overrightarrow{v} \end{aligned}\]

• 고유값(Eigen-Value; $\lambda$) : 고유벡터의 선형변환 전 크기 대비 선형변환 후 크기의 비율

Principal Component Analysis

---

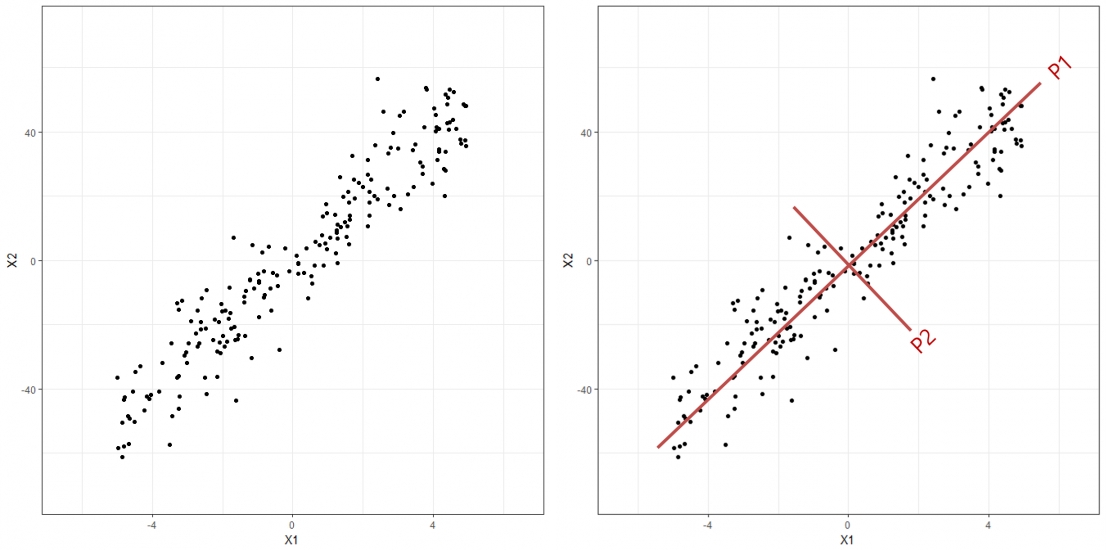
• 주성분 분석(Principal Component Analysis; PCA) : 고차원 데이터에 대하여, X의 방향적 분포를 가장 잘 설명하는 새로운 저차원 직교 좌표를 학습하는 기법

  

  • 주성분(Principal Component; PC) : 새로운 저차원 직교 좌표

• 방법 : 관측치 간 상대적 특성을 잘 보존하는 성분들을 추출함

  

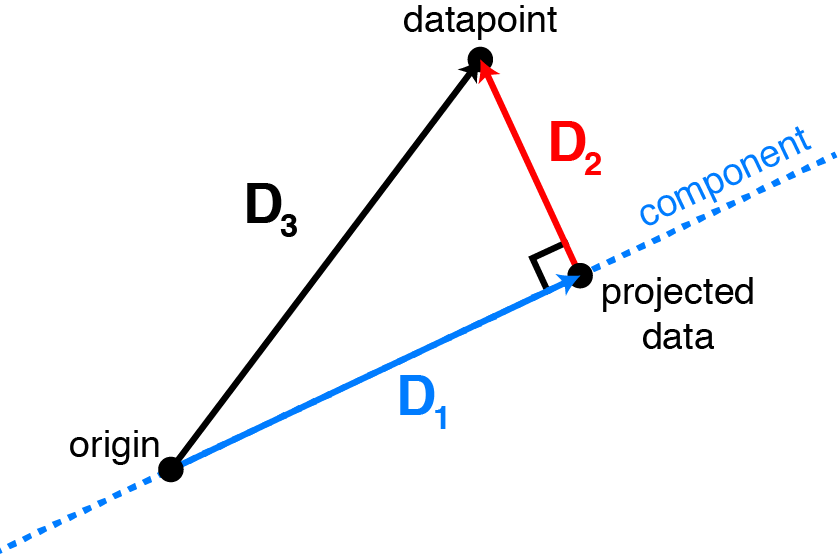
  • $\text{component}$ : 주성분 벡터 $\overrightarrow{w}$
  • $\text{datapoint}$ : 관측치 벡터 $\overrightarrow{x}\in \mathbf{X}$
  • $\text{projected data}$ : 주성분 벡터에 대한 관측치 벡터의 정사영 벡터 $\text{proj}_{\overrightarrow{w}}(\overrightarrow{x})$
  • $D_{1}$ : 관측치 벡터에 대하여 보존하는 정보로서 분산
  • $D_{2}$ : 관측치 벡터에 대하여 유실하는 정보
  • $D_{3}$ : 관측치 벡터의 본래 정보

How to Extract

---

• 관측치 행렬 $X_{N \times P}$ 를 단위벡터 $\overrightarrow{w}$ 에 정사영한다고 하자

  \[\begin{aligned} proj_{\overrightarrow{w}}(\mathbf{X}) &= \frac{<\mathbf{X},\overrightarrow{w}>}{\Vert w \Vert ^2}\cdot\overrightarrow{w}\\ &= (\overrightarrow{w}^{T}\mathbf{X})\cdot\overrightarrow{w} \quad (\because \Vert w \Vert=1) \end{aligned}\]
  • $\overrightarrow{w}$ : 정사영 벡터의 방향
  • $\overrightarrow{w}^{T}\mathbf{X}$ : 정사영 벡터의 크기

• $\overrightarrow{w}$ 에 정사영된 관측치들의 분산 $\mathbf{V}$ 은 다음과 같음

  \[\begin{aligned} \mathbf{V} &= \frac{1}{n}(\overrightarrow{w}^{T}\mathbf{X})(\overrightarrow{w}^{T}\mathbf{X})^{T}\\ &= \frac{1}{n}(\overrightarrow{w}^{T}\mathbf{X}\mathbf{X}^{T}\overrightarrow{w})\\ &= \overrightarrow{w}^{T}\Sigma\overrightarrow{w} \end{aligned}\]
  • $\Sigma=\displaystyle\frac{1}{n}\mathbf{X}\mathbf{X}^{T}$ : 관측치 행렬 $X$ 의 공분산 행렬

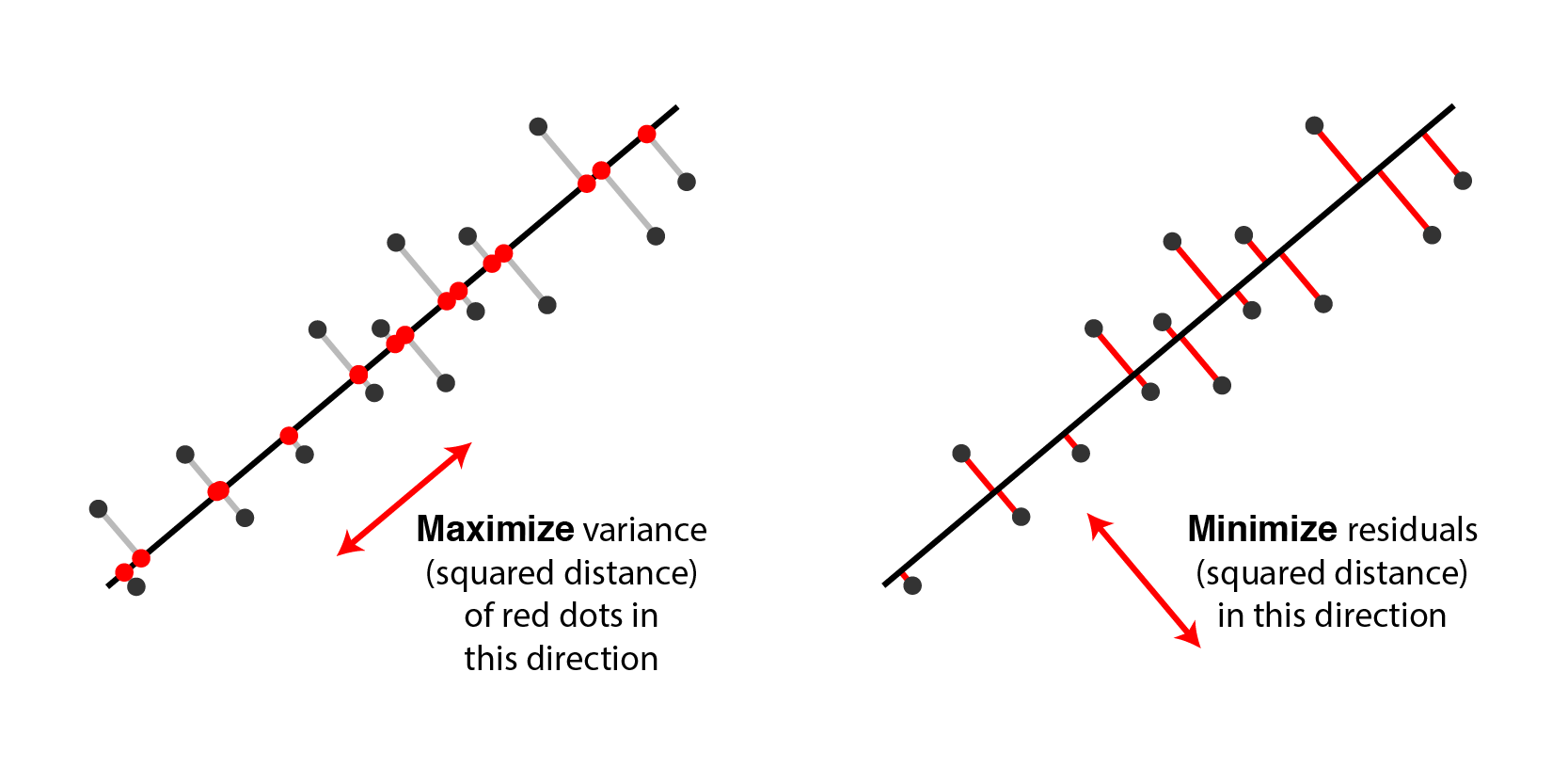
• $\mathbf{V}$ 을 최대화하는 $\overrightarrow{w}$ 를 채택한다고 하자

  \[\hat{\overrightarrow{w}} = \text{arg} \max_{\overrightarrow{w}}{\overrightarrow{w}^{T}\Sigma\overrightarrow{w}} \quad \text{s.t.} \quad \overrightarrow{w}^{T}\overrightarrow{w}=1\]

• 라그랑주 승수법에 기초하여 $\hat{\overrightarrow{w}}$ 도출

  \[\begin{aligned} L(\overrightarrow{w},\lambda) &= \overrightarrow{w}^{T}\Sigma\overrightarrow{w}-\lambda(\overrightarrow{w}^{T}\overrightarrow{w}-1)\\ \frac{\partial L(\overrightarrow{w},\lambda)}{\overrightarrow{w}} &= 0\\ \therefore (\Sigma-\lambda\mathbf{I})\hat{\overrightarrow{w}} &=0 \end{aligned}\]

• $\mathbf{V}$ 를 최대화하는 주성분 $\overrightarrow{w}$ 은 $\mathbf{X}$ 의 공분산 행렬 $\Sigma$ 의 고유벡터임

  \[\begin{aligned} \Sigma &= \mathbb{V}\mathbb{\Lambda}\mathbb{V}^{-1},\\ \mathbb{V} &= \begin{pmatrix}\overrightarrow{w}_{1}&\overrightarrow{w}_{2}&\cdots&\overrightarrow{w}_{p}\end{pmatrix}\\ \mathbb{\Lambda} &= \text{diag}(\lambda_{1},\lambda_{2},\cdots,\lambda_{p}) \end{aligned}\]

Explanatory Power

---

• 주성분 벡터의 고유값 : 관측치 행렬 $\mathbf{X}$ 에 대하여 주성분 벡터에 대한 정사영 벡터 간 분산

  \[\begin{aligned} \mathbf{V} &= \frac{1}{n}(\overrightarrow{w}^{T}\mathbf{X})(\overrightarrow{w}^{T}\mathbf{X})^{T}\\ &= \frac{1}{n}\overrightarrow{w}^{T}\mathbf{X}\mathbf{X}^{T}\overrightarrow{w}\\ &= \overrightarrow{w}^{T}\Sigma\overrightarrow{w}\\ &= \hat{\overrightarrow{w}}^{T}\lambda\hat{\overrightarrow{w}} \quad (\because \Sigma\hat{\overrightarrow{w}}-\lambda\hat{\overrightarrow{w}}=0)\\ &= \lambda \quad (\because \overrightarrow{w}^{T}\overrightarrow{w}=1) \end{aligned}\]

• 주성분 벡터의 설명력 : 관측치 행렬 $\mathbf{X}_{N \times P}$ 에 대하여 생성 가능한 $P$ 개의 주성분 벡터 고유값 합계 대비 해당 주성분 벡터 고유값 비율

  \[\frac{\lambda_{k}}{\sum_{i=1}^{p}{\lambda_{i}}}\]

---

이미지 출처

• http://alexhwilliams.info/itsneuronalblog/2016/03/27/pca/