Partial Derivative

Partial Derivative

---

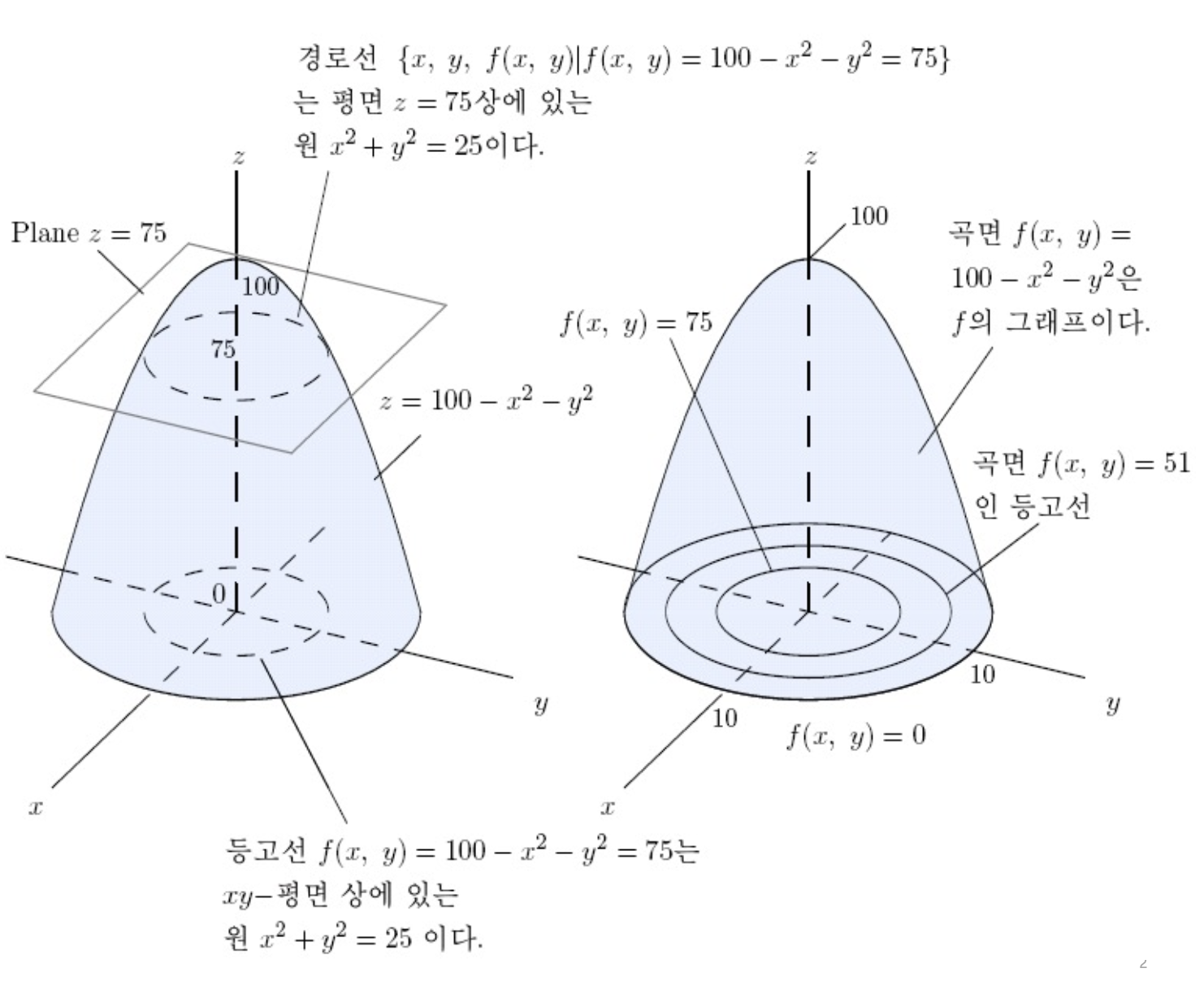
• 2변수함수 \(y=f(x,z)\) 는 $XYZ$-공간에서의 곡면임

  

  \[\begin{aligned} \left\{(x,y,z) \mid (x,z) \in D(f)\right\} \end{aligned}\]

• 편미분(Partial Derivative): 다변수함수 $y=f(x,z)$ 에 대하여, 변수 $x$ 를 제외한 다른 변수들을 상수로 고정하였을 때, $x$ 의 단위 변화에 따른 $y$ 의 순간변화율

  \[\begin{aligned} \frac{\partial}{\partial x}f(x,z) &= \lim_{\Delta x \to 0}{\frac{f(x+\Delta x,z)-f(x,z)}{\Delta x}} \end{aligned}\]

• 고계편도함수(Partial Derivative Function): 다변수함수에 대하여 그 편도함수의 편도함수

  • 1계편도함수:

    \[\begin{aligned} f_{X}(x,z) &= \frac{\partial}{\partial x}f(x,z)\\ f_{Z}(x,z) &= \frac{\partial}{\partial z}f(x,z) \end{aligned}\]

  • 2계편도함수:

    \[\begin{aligned} (f_{X})_{X} &= f_{XX}(x,z) = \frac{\partial^{2}}{\partial x^{2}}f(x,z)\\ (f_{Z})_{Z} &= f_{ZZ}(x,z) = \frac{\partial^{2}}{\partial z^{2}}f(x,z)\\ (f_{X})_{Z} &= f_{XZ}(x,z) = \frac{\partial^{2}}{\partial x \partial z}f(x,z)\\ (f_{Z})_{X} &= f_{ZX}(x,z) = \frac{\partial^{2}}{\partial z \partial x}f(x,z) \end{aligned}\]

• 헤시안 행렬(Hessian Matrix): 다변수함수의 고계편도함수를 표현한 행렬

  \[\begin{aligned} D^{2}f(x,z) &:=\begin{bmatrix} f_{XX} & f_{XZ}\\ f_{XZ} & f_{ZZ} \end{bmatrix} \end{aligned}\]

• 그라디언트(Gradient): $N$ 변수함수 $y=f(x_{1},x_{2},\cdots,x_{N})$ 에 대하여 각 변수에 대한 일계편도함수로 구성된 벡터

  

  \[\begin{aligned} \nabla f &= \begin{bmatrix} \displaystyle\frac{\partial f}{\partial x_{1}} & \displaystyle\frac{\partial f}{\partial x_{2}} & \cdots & \displaystyle\frac{\partial f}{\partial x_{N}} \end{bmatrix}^{T} \end{aligned}\]
  • \(\nabla f \vert_{(x_{1},x_{2},\cdots,x_{n})}\) 는 점 \((x_{1},x_{2},\cdots,x_{n})\) 에서 \(f\) 의 값이 가장 가파르게 증가하는 방향임

Critical Point

---

• 임계점(Critical Point) : 함수의 1계편도함수 값이 $0$ 이거나 존재하지 않는 지점

  \[\begin{aligned} f_{X} = 0, \quad f_{Z} = 0 \end{aligned}\]

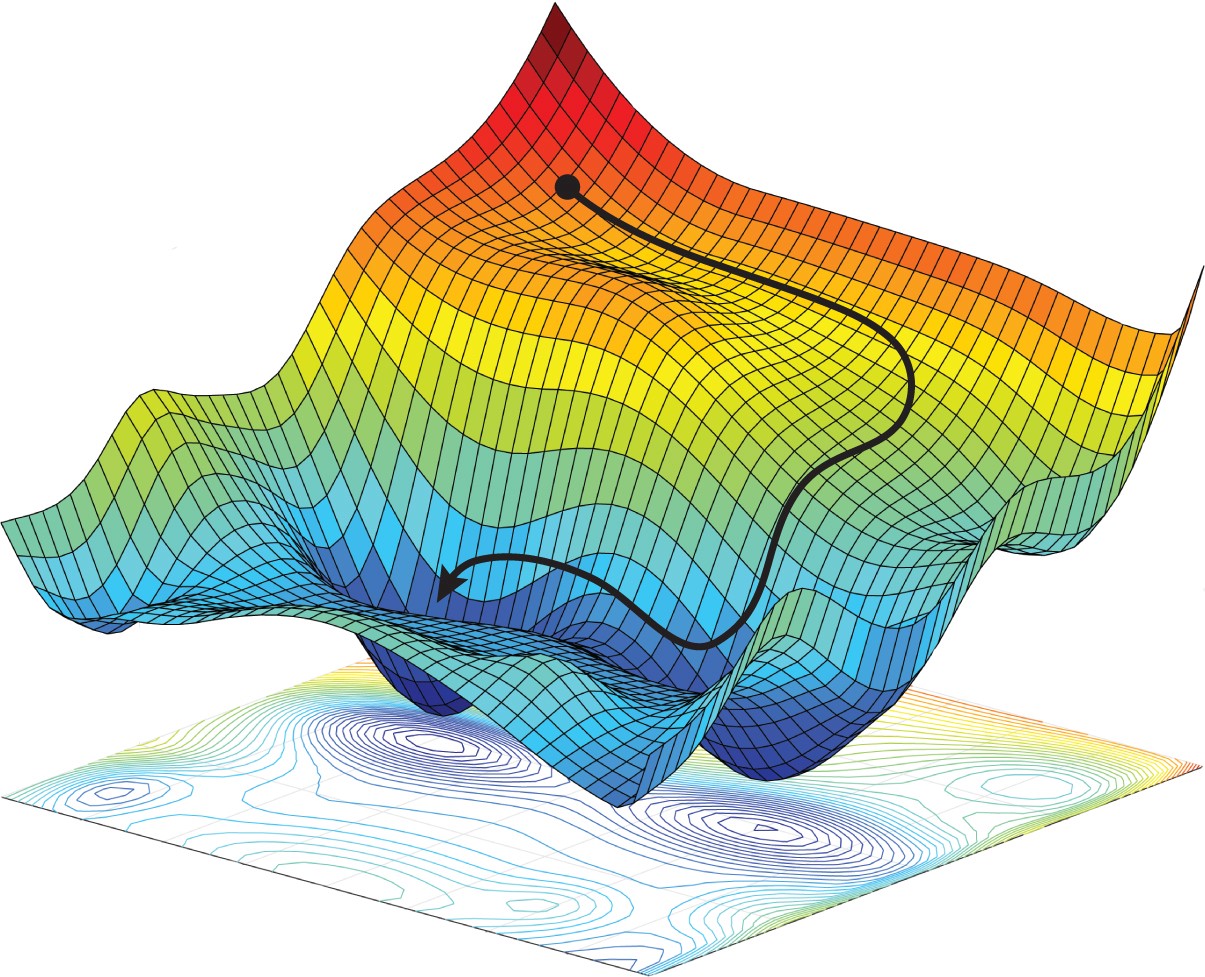
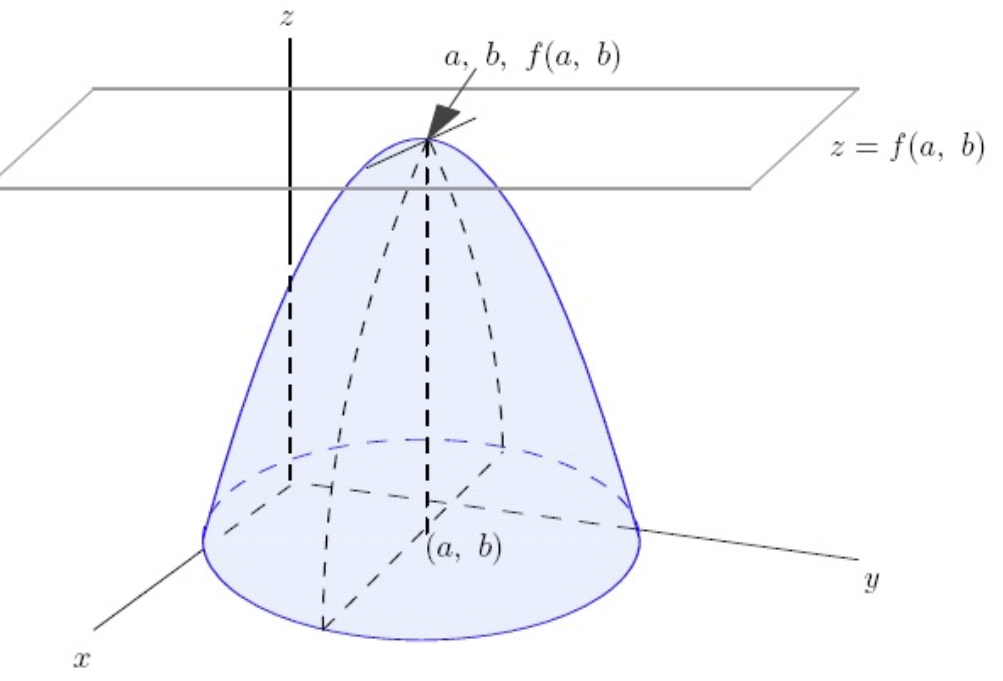
• 극점(Local Extremum Point) : 임계점 중에서 극값을 갖는 지점으로서, $f$ 의 임계점 $(a,b)$ 의 모든 열린 근방 $(x,z)$ 에 대하여 다음 중 하나만을 만족하는 경우

  

  \[\begin{cases} f(a,b) \leq f(x,z) \quad &\text{maximum}\\ f(a,b) \geq f(x,z) \quad &\text{minimum} \end{cases}\]

• 안장점(Saddle Point) : 임계점 중에서 극값을 갖지 않는 점으로서, 어떤 측면에서는 극소값이 되고, 동시에 다른 측면에서는 극대값이 되는 지점

  

  \[\begin{aligned} f(a,b) \leq f(x,z) \quad \text{and} \quad f(a,b) \geq f(x,z) \end{aligned}\]

• 헤시안 행렬식 값에 따른 극값 판별:

  \[\begin{aligned} \Delta &= \mathrm{det}(D^{2}f(x,z)\vert_{(a,b)})\\ &= f_{XX}(x,b)\vert_{x=a} \cdot f_{ZZ}(a,z)\vert_{z=b}-f^{2}_{XZ}(x,z)\vert_{(a,b)} \end{aligned}\]
  • $\Delta = 0$: 극값의 존재 여부를 결정할 수 없음
  • $\Delta < 0$: $(a,b)$ 에서 안장점을 가짐
  • $\Delta > 0$: $(a,b)$ 에서 극값을 가짐