Prior Determination

Prior Determination

---

• 사전 확률 분포의 결정은 모델링의 일부임

  모형이 적합한 이후에는 사후 확률 분포를 살펴보아야 하고, 이치에 맞는지 확인해야 한다. 만일 사후 확률 분포가 이치에 맞지 않는다면 모형에 포함되지 않은 사전 정보가 추가로 필요하다는 것을 의미한다. 그리고 이전에 사용한 사전 확률 분포의 가정에 위배된다는 것을 의미한다. 그래서 이전으로 돌아가 사전 확률 분포가 외부 정보와 조화되도록 변경하는 것이 적절하다. (Andrew Gelman)

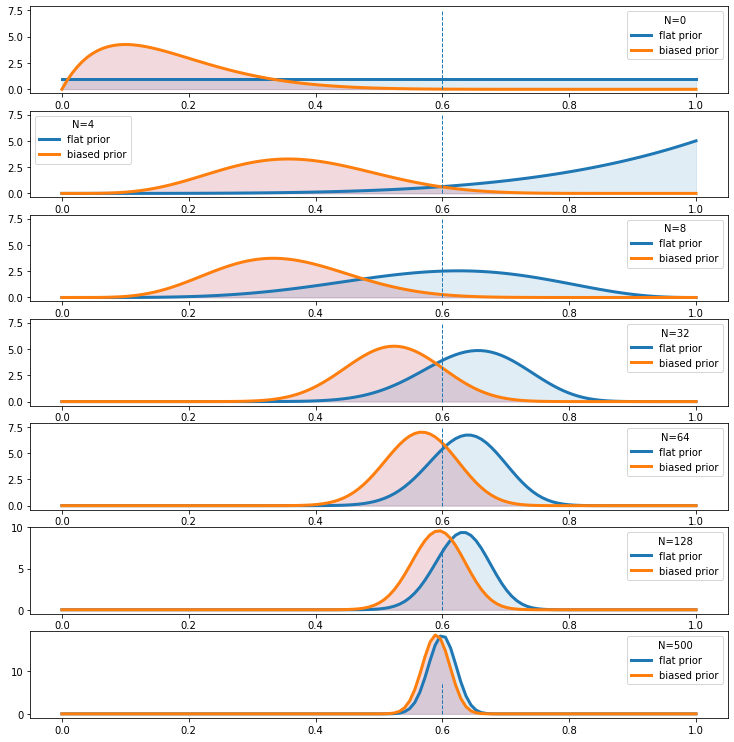
• 관측치 갯수($N$)가 많아질수록 사전 확률 분포의 영향력이 약화됨

  

  동전의 미래 행위에 대한 당신의 견해가 이웃 사람의 견해와 크게 다르더라도, 당신의 견해와 이웃 사람의 견해는 일상적으로 실험적인 던지기의 긴 연속에 베이즈의 정리를 적용하여 변형되어 거의 구별할 수 없게 될 것이다(Edwards, Lindman, and Savage, 1963, p.197). 즉, 다양한 신념들은 충분한 근거가 주어지면 간주관적으로 수렴하며, 이 일치를 객관적 신념 상태로 해석할 수 있다.

Non-Informative Dist.

---

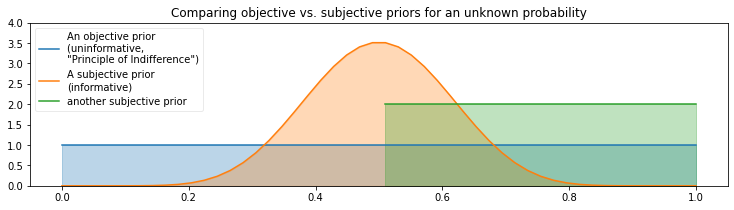
• Principle of Indifference : 가능한 모수 공간에서 특별히 어떤 값을 선호하지 않는 원칙에 따라, 관측치가 사후분포에 미치는 영향력을 최대화하는 방법

  무차별의 원리가 주장하는 것은 만약 우리의 관심의 대상이 여러 가지 대안 중 어느 것보다 더 예측할 만한 어떠한 알려진 이유가 없다면 그러한 지식에 상대적으로 이러한 대안 각각에 대한 주장들은 동일한 확률을 갖는다는 점이다(Keynes, 1921, p.42).

  \[\begin{aligned} X \mid \theta &\sim \text{Binomial}(n,\theta)\\ \theta &\sim \text{Uniform}(0,1) \end{aligned}\]

Transformation Variant of Flat Prior Dist.

• 모수 $\theta$ 가 균등 분포 $\text{Uniform}(0,1)$ 를 따르는 객관적인 사전확률이라고 하자

  \[\theta \sim \text{Uniform}(0,1)\]

• 모수 $\theta$ 를 $\log{\displaystyle\frac{\theta}{1-\theta}}$ 로 변수 변환한 $\psi$ 는 로지스틱 분포 $\text{Logistic}(0,1)$ 을 따르게 됨

  \[\begin{aligned} \psi &= g(\theta)\\ &= \log{\frac{\theta}{1-\theta}}\\ \\ \theta &= g^{-1}(\psi)\\ &= \frac{\text{exp}(\psi)}{1+\text{exp}(\psi)}\\ \\ f_{\psi}(\psi) &= f_{\theta}(g^{-1}(\psi)) \times \left\vert \frac{\text{d}}{\text{d} \psi}g^{-1}(\psi)\right\vert \\ &= 1 \times \left\vert \frac{\text{d}}{\text{d} \psi}g^{-1}(\psi) \right\vert \quad (\because \theta \sim \text{Uniform}(0,1))\\ &= \frac{\text{exp}(\psi)}{(1+\text{exp}(\psi))^{2}}\\ \\ \therefore \psi &\sim \text{Logistic}(0,1) \end{aligned}\]

• 즉, 모수 $\theta$ 의 변수 변환에 의하여 사전분포의 객관성이 상실되었음

  • 변환 전 : $\theta \sim \text{Uniform}(0,1)$

    

  • 변환 후 : $\psi \sim \text{Logistic}(0,1)$

    

Jacobian Change of Variables

• 자코비안 변수 변환(Jacobian Change of Variables) : 기본 변수 $\overrightarrow{\theta}$, 변환 변수 $\overrightarrow{\psi}=g(\overrightarrow{\theta})$ 및 그 밀도 함수 $f$ 에 대하여, 다음을 만족하는 변수 변환 방법

  \[\begin{aligned} f_{\psi}\left(\psi\right) &=f_{\theta}\left(\theta\right) \cdot \left\vert \frac{1}{\text{det}\left(\mathbb{J}\right)} \right\vert\\ \overrightarrow{\theta} &= \begin{pmatrix} \theta_{1} & \theta_{2} & \cdots & \theta_{n} \end{pmatrix}\\ \overrightarrow{\psi} &= \begin{pmatrix} \psi_{1} & \psi_{2} & \cdots & \psi_{m} \end{pmatrix} \end{aligned}\]

  • 자코비안 행렬(Jacobian Matrix; $\mathbb{J}$) : 다변수 벡터 값 함수의 모든 편미분을 모아 만든 행렬

    \[\begin{aligned} \mathbb{J} = \frac{\partial \psi}{\partial \theta} = \begin{pmatrix} \displaystyle\frac{\partial \psi_1}{\partial \theta_1} & \displaystyle\frac{\partial \psi_1}{\partial \theta_2} & \cdots & \displaystyle\frac{\partial \psi_1}{\partial \theta_n}\\ \displaystyle\frac{\partial \psi_2}{\partial \theta_1} & \displaystyle\frac{\partial \psi_2}{\partial \theta_2} & \cdots & \displaystyle\frac{\partial \psi_2}{\partial \theta_n}\\ \vdots & \vdots & \ddots & \vdots\\ \displaystyle\frac{\partial \psi_m}{\partial \theta_1} & \displaystyle\frac{\partial \psi_m}{\partial \theta_2} & \cdots & \displaystyle\frac{\partial \psi_m}{\partial \theta_n} \end{pmatrix} \end{aligned}\]

• 변환 변수 $\psi=g(\theta)$ 가 기본 변수에 대하여 (확률) 밀도의 불변성을 보장한다고 하자

  \[\begin{aligned} P(a \le \theta \le b) &= P(g(a) \le \psi \le g(b))\\ \int_{a}^{b}{f_{\theta}(\theta)d\theta} &= \int_{g(a)}^{g(b)}{f_{\psi}(\psi)d\psi} \end{aligned}\]

• 기본 변수의 단위당 밀도와 변환 변수의 단위당 밀도가 동일함

  \[f_{\theta}(\theta) \cdot \Delta\theta =f_{\psi}(\psi) \cdot \Delta\psi\]

• $\because \Delta\psi=\displaystyle\frac{\Delta\psi}{\Delta\theta} \cdot \Delta\theta$

  \[\begin{aligned} f_{\psi}(\psi) \cdot \Delta\psi &= f_{\psi}(\psi) \cdot \left(\frac{\Delta\psi}{\Delta\theta} \cdot \Delta\theta\right)\\ &= f_{\theta}(\theta) \cdot \Delta\theta \end{aligned}\]

• 따라서 자코비안 변수 변환은 밀도의 불변성을 보장함

  \[\begin{aligned} f_{\psi}(\psi) \cdot \left(\frac{\Delta\psi}{\Delta\theta} \cdot \Delta\theta\right) &= f_{\theta}(\theta) \cdot \Delta\theta\\ f_{\psi}(\psi) \cdot \left\vert \frac{\Delta\psi}{\Delta\theta} \right\vert &= f_{\theta}(\theta)\\ \therefore f_{\psi}(\psi) &= f_{\theta}(\theta) \cdot \left\vert \frac{\Delta\theta}{\Delta\psi} \right\vert \end{aligned}\]

Jeffreys Priors

• Jeffreys Priors : 모수 공간에 대해 불변성을 보장함으로써 변수 변환 후에도 객관성을 보존하는 사전분포

  \[\pi_{J}(\theta) \propto \sqrt{\mathbf{I}(\theta)}\]

  • $\sqrt{\mathbf{I}(\theta)}$ : Fisher Information

    \[\begin{aligned} \mathbf{I}(\theta) = \mathbb{E}\left[\frac{\text{d}^{2}}{\text{d}\theta^{2}}\log{\mathcal{L}(\theta)}\right] = \mathbb{E}\left[\left(\frac{\partial \log{\mathcal{L}(\theta)}}{\partial \theta}\right)^{2}\right] \end{aligned}\]

• 변수 $\theta$ 에 대한 확률분포가 그 피셔 정보의 자승근에 비례하도록 정의되었다고 하자

  \[p(\theta) \propto \sqrt{I(\theta)}\]

• 함수 $g$ 를 통해 변수 $\theta$ 를 변수 $\psi$ 로 변환한다고 하자

  \[\psi = g(\theta)\]

• 변환 변수 $\psi$ 의 확률분포 또한 그 피셔 정보의 자승근에 비례하게 됨

  \[p(\psi) \propto \sqrt{I(\psi)}\]

• 미분 법칙에 의해 다음이 성립함

  \[\frac{\partial \log{\mathcal{L}(\psi)}}{\partial \psi} =\frac{\partial \log{\mathcal{L}(\theta)}}{\partial \theta} \cdot \frac{\partial \theta}{\partial \psi}\]

• 변환 변수 $\psi$ 의 피셔 정보 $I(\psi)$ 는 다음과 같음

  \[\begin{aligned} I(\psi) &=\mathbb{E}\left[\left(\frac{\partial \log{\mathcal{L}(\theta)}}{\partial \theta} \cdot \frac{\partial \theta}{\partial \psi} \right)^{2}\right]\\ &=\mathbb{E}\left[\left(\frac{\partial \log{\mathcal{L}(\theta)}}{\theta}\right)^{2}\right] \cdot \left(\frac{d\theta}{d\psi}\right)^{2}\\ &=I(\theta) \cdot \left(\frac{d\theta}{d\psi}\right)^{2} \end{aligned}\]

• 따라서 변환 변수 $\psi$ 의 확률분포는 기본 변수 $\theta$ 의 확률분포의 형태를 유지하되,
  자코비안 행렬식 $\left\vert \displaystyle\frac{d\theta}{d\psi} \right\vert$ 로 보정된 양상을 띠게 됨

  \[\begin{aligned} p(\psi) &\propto \sqrt{I(\psi)}\\ &= \sqrt{I(\theta) \cdot \left(\frac{d\theta}{d\psi}\right)^{2}}\\ &= \sqrt{I(\theta)} \cdot \left\vert \frac{d\theta}{d\psi} \right\vert \end{aligned}\]

Empirical Bayes

---

• 실증적 베이즈(Empirical Bayes): 사전 확률 분포를 빈도주의적으로 접근하여 추정하는 방법으로서, 사전 정보가 많지 않지만 관측치가 풍부한 경우 유용하나, 사전 정보가 관측하기 이전에 정의되어야 한다는 원칙에 위배됨

  그러므로 하나의 의견이 주어지면, 우리는 진위에 근거하여 그것을 칭찬하거나 책망할 수 있을 뿐이다. 특정한 형태의 습관이 주어지면 우리는 습관이 산출하는 신념도가 그것이 진리로 이끄는 실제 비율에 근접하거나 멀어지는가에 따라서 칭찬하거나 책망할 수 있다. 그렇다면 우리는 의견을 산출하는 습관들을 칭찬하거나 책망하는 것으로부터 파생적으로 의견들을 칭찬하거나 책망할 수 있다(Ramsey, 1926, p.51).

• example General Model

  \[\begin{aligned} X_{i} \mid \theta &\sim N(\theta, 5^2)\\ \theta &\sim N(\mu, \sigma^2) \end{aligned}\]

• Objective Prior:

  \[\theta \sim N(0, 100^2)\]

• Subjective Prior:

  \[\theta \sim N(\mu_{0}, \sigma_{0}^{2})\]

• Empirical Bayes:

  \[\theta \sim N\left(\frac{1}{N}\sum_{i=1}^{N}{X_i}, \frac{1}{N-1}\sum_{i=1}^{N}{(X_i-\mu)^2}\right)\]

Conjugate Priors

---

• 켤레 사전 분포(Conjugate Priors): 관측치 $X$ 와 그 확률분포 \(\mathcal{L}_{\alpha}\) 에 대하여, 다음의 조건을 만족하는 사전확률분포 \(\pi_{\beta}\) 가 존재하는 경우, \(\pi_{\beta}\) 를 \(\mathcal{L}_{\alpha}\) 의 켤레 사전 분포(Conjugate Prior Dist.)라고 함

  \[\begin{aligned} \pi_{\beta^{\prime}}(\theta \mid X) \propto \mathcal{L}_{\alpha}(\theta) \cdot \pi_{\beta}(\theta) \end{aligned}\]
  • $\mathcal{L}_{\alpha}(\theta)$ : 모수 $\theta$ 의 우도 함수
  • $\pi_{\beta}(\theta)$ : 모수 $\theta$ 의 사전 확률
  • $\pi_{\beta^{\prime}}(\theta \mid X)$ : 모수 $\theta$ 의 사후 확률
  • $\alpha,\beta,\beta^{\prime}$ : 모수들의 집합

• 예시

  Likelihood	Prior	Posterior
  $\text{Bernoulli}(\theta)$	$\text{Beta}(\alpha, \beta)$	$\text{Beta}\Big(\alpha + n \cdot \bar{x}, \beta + n\cdot(1-\bar{x})\Big)$
  $\text{Poisson}(\lambda)$	$\text{Gamma}(\alpha, \beta)$	$\text{Gamma}(\alpha+ n \cdot \bar{x}, \beta+n)$
  $\text{Multinomial}(\theta)$	$\text{Dirichlet}(\alpha)$	$\text{Dirichlet}(\alpha+n \cdot \bar{x})$
  $N(\mu, \sigma^2)$ $\text{known} \; \sigma^2$	$N(\mu_0, \sigma_0^2)$	$N\Bigg( \displaystyle\frac{\displaystyle\frac{\mu_0}{\sigma_0^2} + \frac{n \cdot \bar{x}}{\sigma^2}}{\displaystyle\frac{1}{\sigma_0^2} + \displaystyle\frac{n}{\sigma^2}}, \displaystyle\frac{1}{\displaystyle\frac{1}{\sigma_0^2} + \frac{n}{\sigma^2}} \Bigg)$
  $N(\mu, \sigma^2)$ $\text{known} \; \mu$	$\text{Inv-Gamma}(\alpha, \beta)$	$\text{Inv-Gamma}\Bigg(\alpha + \displaystyle\frac{n}{2}, \beta + \displaystyle\frac{n \cdot (\bar{x} -\mu)^2}{2}\Bigg)$
  $N(\mu, \Sigma)$ $\text{known} \; \mu$	$\text{Inv-Wishart}(\nu_{0}, S_{0})$	$\text{Inv-Wishart}(\nu_{0}+n, S_{0} + n \cdot \bar{S})$