Prob. Dist. Functions

Discrete Prob. Dist.

---

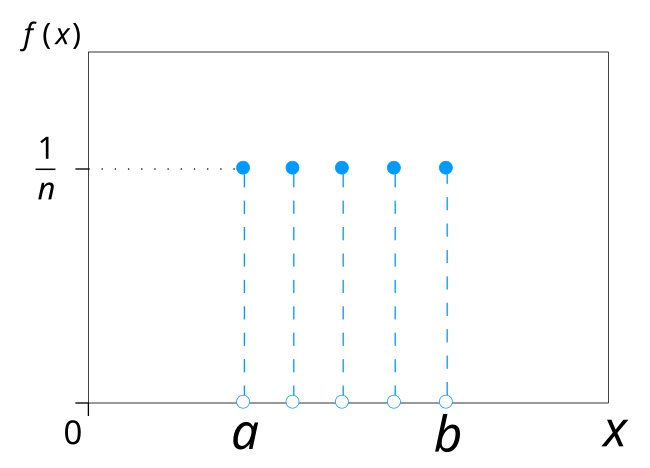
이산 균등 분포(Discrete Uniform Dist.)

• 정의 : 실현 가능한 각각의 결과가 동일한 확률로 발생하는 분포

  \[X \sim \text{DiscreteUniform}(a,b)\]
  • $1,2,3,4,5,6$ 까지 눈금이 있는 주사위를 굴릴 때, 각 눈금이 나올 확률의 분포

• 확률 질량 함수(Prob. Mass Function, PMF)

  \[P(X=k)=\frac{1}{n}\]
  • $X$ : 이산 균등 분포를 따르는 확률변수
  • $k=a,\cdots,b$ : 발생 가능한 결과
  • $n$ : 발생 가능한 결과의 갯수

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=\frac{a+b}{2}\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big]=\frac{(b-a+1)^2-1}{12}\]

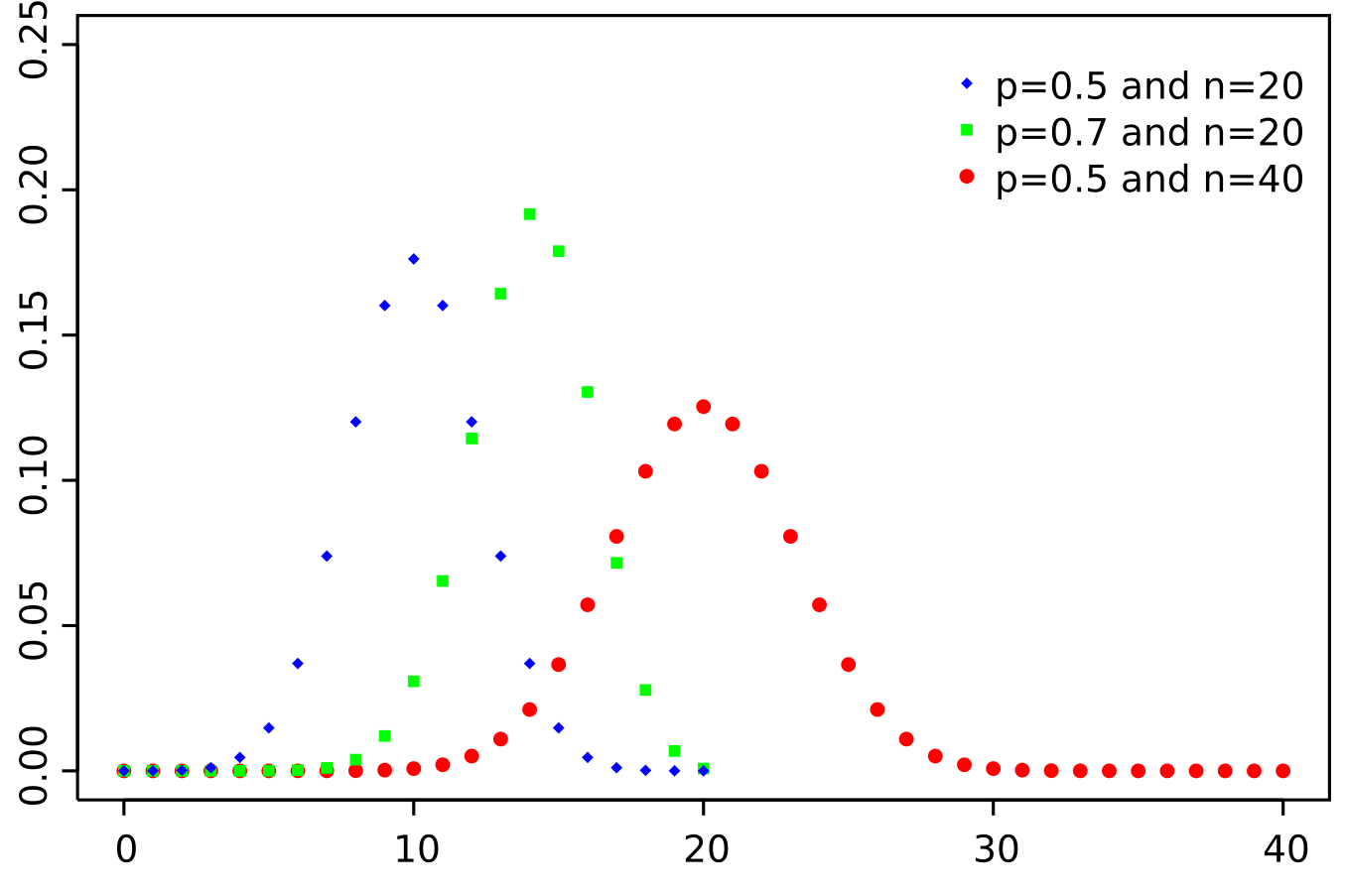
이항 분포(Bi-Nomial Dist.)

• 정의 : 고정된 횟수($n$)의 독립적인 베르누이 시행에서 성공 횟수를 나타내는 분포

  \[X \sim \text{Bin}(n,p)\]
  • 열 번의 동전 던지기 실험에서 앞면이 나오는 횟수가 특정 값일 확률의 분포

• 확률 질량 함수(Prob. Mass Function, PMF)

  \[P(X=k) = \begin{pmatrix}n\\ k\\ \end{pmatrix} p^{k} \cdot (1-p)^{n-k}\]
  • $X$ : 이항 분포를 따르는 확률변수
  • $k=0,1,2,\cdots,n$ : 성공 횟수
  • $p$ : 성공 가능성
  • $n$ : 베르누이 시행 횟수

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=n \cdot p\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big]=n \cdot p \cdot (1-p)\]

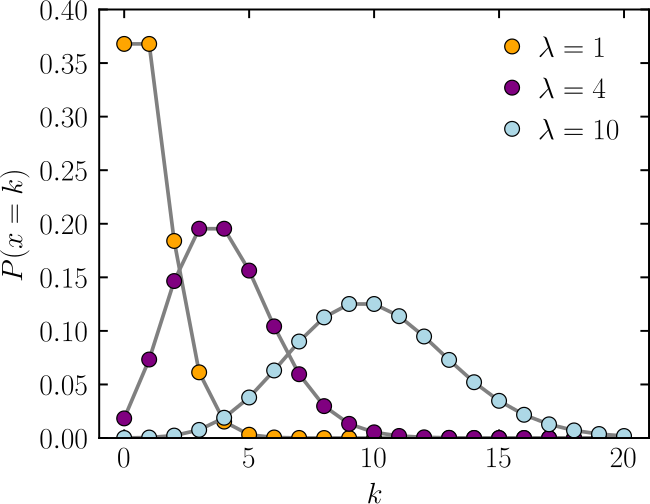
포아송 분포(Poisson Dist.)

• 정의 : 단위 시간 혹은 공간 안에서 사건 발생 횟수를 나타내는 분포

  \[X \sim \text{Poi}(\lambda)\]
  • 한 시간 동안 특정 웹사이트에 접속하는 사용자 수가 특정 값일 확률의 분포

• 확률 질량 함수(Prob. Mass Function, PMF)

  \[P(X=k) = \frac{\lambda^{k}}{k!}\text{exp}(-\lambda)\]
  • $X$ : 포아송 분포를 따르는 확률변수
  • $k=0,1,2,\cdots,n$ : 단위 시간 혹은 공간 안에서 사건 발생 횟수
  • $\lambda$ : 단위 시간 혹은 공간 안에서 평균 사건 발생 횟수

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=\lambda\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big]=\lambda\]

다항 분포(Multi-Nomial Dist.)

• 정의 : 여러 카테고리의 결과가 있는 일련의 실험에서 각 카테고리 결과의 횟수를 나타내는 분포

  \[X \sim \text{Multin}(n;p_1, \cdots, p_k)\]
  • 설문조사에서 예, 아니오, 무응답 응답자 수가 특정 값일 확률을 나타내는 분포

• 확률 질량 함수(Prob. Mass Function, PMF)

  \[P(X_1=x_1, \cdots, X_k=x_k) = {n \choose x_{1} ~ \cdots ~ x_{k}} p_{1}^{x_{1}} \cdots p_{k}^{x_{k}}\]
  • $X$ : 다항 분포를 따르는 확률변수
  • $x_i=0,1,2,\cdots,n$ : $i$ 번째 카테고리의 성공 횟수
  • $p_{i}$ : $i$ 번째 카테고리의 성공 가능성
  • $\sum_{i}{x_{i}}=n$ : 시행 횟수

• 기대값(Expected Value)

  \[\mathbb{E}\big[X_{i}\big]=n \cdot p_{i}\]

• 분산(Variance)

  \[\mathbb{V}\big[X_{i}\big]=n \cdot p_{i} \cdot (1-p_{i})\]

• 공분산(Covariance)

  \[\mathbb{Cov}\big[X_{i},X_{j}\big]=-n \cdot p_{i} \cdot p_{j}\]

Continuous Prob. Dist.

---

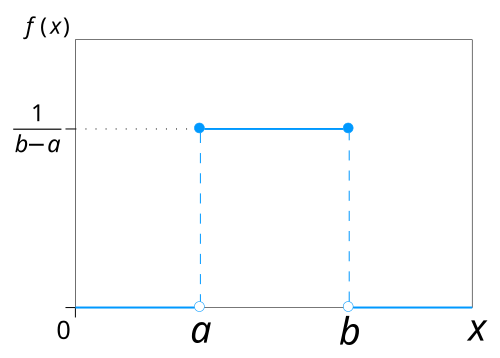
균등 분포(Uniform Dist.)

• 정의 : 주어진 구간에서 모든 값이 일정한 확률을 가지는 분포

  \[X \sim \text{Uniform}(a,b)\]
  • $0$ 과 $1$ 사이의 수를 무작위로 선택할 때, 특정 값이 선택될 확률의 분포

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[P(X=x) = \frac{1}{b-a} \quad \text{for}\;a<x<b\]

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=\frac{a+b}{2}\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big]=\frac{(b-a)^2}{12}\]

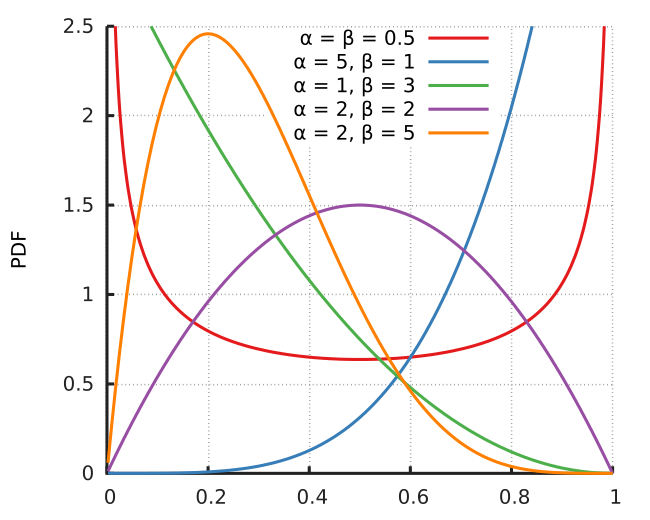
베타 분포(Beta Dist.)

• 정의 : 두 매개변수 $\alpha$ 와 $\beta$ 에 의해 모양이 결정되는, $0$ 과 $1$ 사이의 값에 대한 확률 분포

  \[X \sim \text{Beta}(\alpha,\beta)\]
  • 어떤 사건의 성공 횟수($\alpha$)와 실패 횟수($\beta$)가 주어졌을 때, 해당 사건의 성공 가능성이 특정 값일 확률에 대한 분포

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[P(X=x) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)} x^{\alpha-1} (1-x)^{\beta-1}\]
  • $X$ : 베타 분포를 따르는 확률 변수
  • $x$ : 주로 성공 가능성
  • $\alpha$ : 주로 성공 횟수로서, 클수록 우편향된 형태의 분포가 됨
  • $\beta$ : 주로 실패 횟수로서, 클수록 좌편향된 형태의 분포가 됨

  • $\Gamma(\cdot)$ : 감마 함수

    \[\begin{aligned} \Gamma(n) &= \int_{0}^{\infty}{t^{n-1}e^{-t}}\text{d}t\\ &= (n-1)! \quad \text{s.t.}\;n \in \mathbf{Z}^{+} \end{aligned}\]

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=\frac{\alpha}{\alpha+\beta}\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big]=\frac{\alpha \cdot \beta}{(\alpha+\beta)^2 \cdot (\alpha+\beta+1)}\]

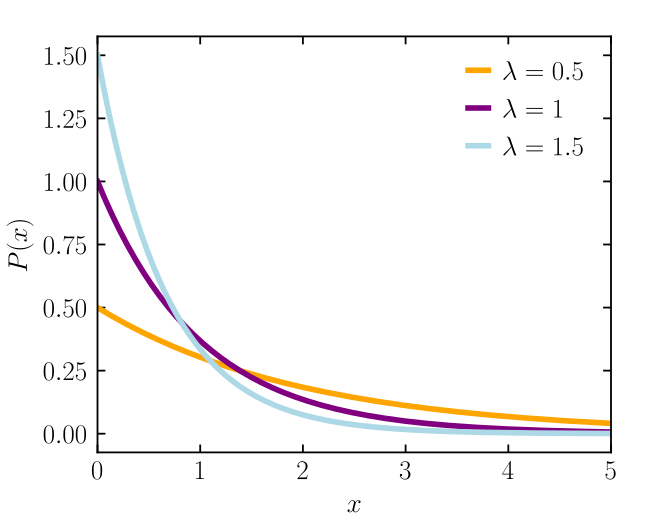
지수 분포(Exponential Dist.)

• 정의 : 단일 사건의 대기 시간을 나타내는 분포

  \[X \sim \text{Exp}(\lambda)\]
  • 특정 버스 정류장에서 버스가 도착할 때까지 대기 시간이 특정 값일 확률에 대한 분포

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[P(X=x) = \lambda \cdot \text{exp}(-\lambda \cdot x)\]
  • $X$ : 지수 분포를 따르는 확률 변수
  • $x$ : 대기 시간
  • $\lambda$ : 단위 시간 당 사건 발생률

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=\frac{1}{\lambda}\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big]=\frac{1}{\lambda^{2}}\]

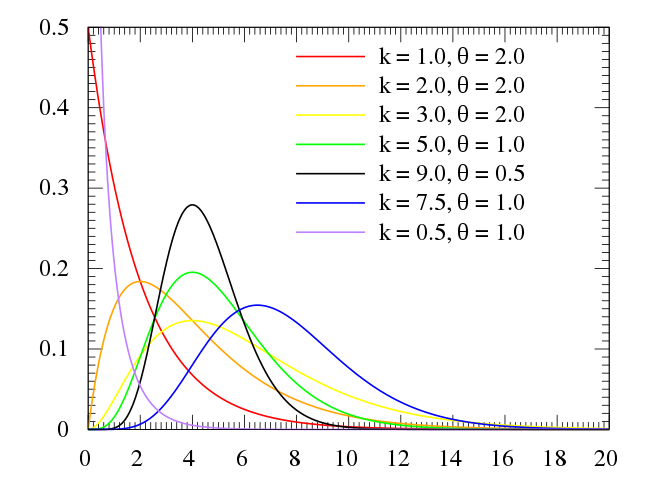
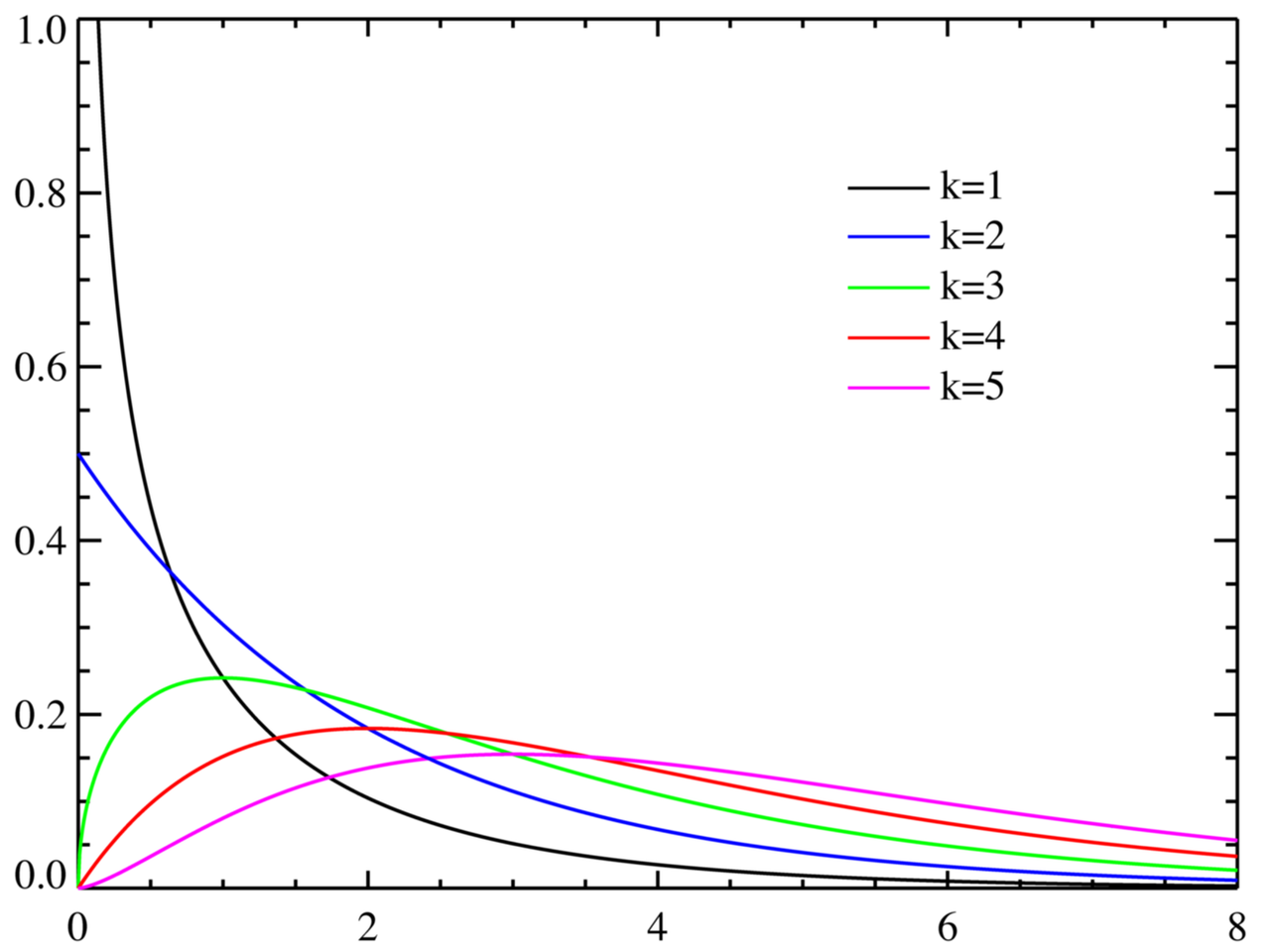
감마 분포(Gamma Dist.)

• 정의 : 여러 지수적 사건의 총 대기 시간을 나타내는 분포

  \[X \sim \text{Gamma}(k, \theta)\]
  • (여러 부품이 결합된) 특정 기계가 고장 나기 전까지 작동하는 시간이 특정 값일 확률 대한 분포

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[P(X=x) = \frac{x^{k-1}\exp\left(-\frac{x}{\theta}\right)}{\theta^{k} \cdot \Gamma(k)}\]
  • $X$ : 감마 분포를 따르는 확률 변수
  • $x > 0$ : 총 대기 시간
  • $k$ : 형태 매개변수로서, 지수적 사건 발생 횟수
  • $\theta$ : 스케일 매개변수로서, 지수적 사건의 평균 대기 시간
  • $\Gamma(\cdot)$ : 감마 함수

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=k \cdot \theta\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big]=k \cdot \theta^{2}\]

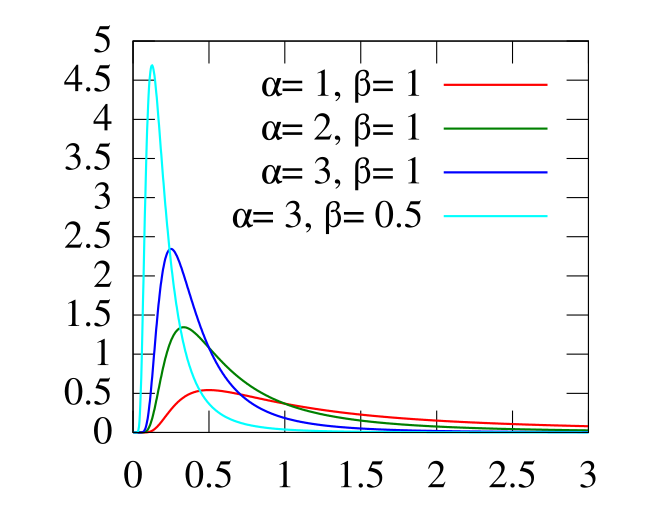
역감마 분포(Inverse-Gamma Dist.)

• 정의 : 감마 분포의 역수를 따르는 확률 분포

  \[\begin{aligned} X &\sim \text{Gamma}(k, \theta)\\ \frac{1}{X} &\sim \text{Inv-Gamma}(k, \theta) \end{aligned}\]
  • 정규 분포 $N(\mu, \sigma^2)$ 의 분산 $\sigma^2$ 에 대한 사전확률분포

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[P(Y=y) = \frac{\theta^{k} \cdot y^{-k-1} \cdot \exp\left(-\frac{\theta}{y}\right)}{\Gamma(k)}\]
  • $Y=\displaystyle\frac{1}{X}$ : 역감마 분포를 따르는 확률 변수
  • $k$ : 형태 매개변수
  • $\theta$ : 스케일 매개변수
  • $\Gamma(\cdot)$ : 감마 함수

• 기대값(Expected Value)

  \[\mathbb{E}\big[Y\big]=\frac{\theta}{k-1} \quad \text{s.t.}\; k>1\]

• 분산(Variance)

  \[\mathbb{V}\big[Y\big]=\frac{\theta^2}{(k-1)^2(k-2)} \quad \text{s.t.}\; k>2\]

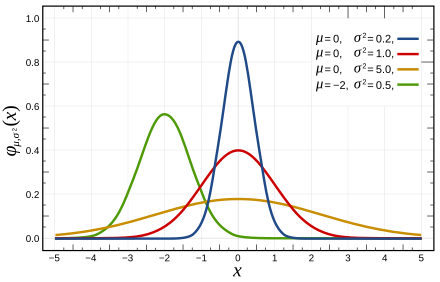
정규 분포(Normal Dist.)

• 정의 : 자연 및 사회 과학에서 발생하는 대부분의 현상을 설명하는 대표적인 분포

  \[X \sim N(\mu, \sigma^2)\]

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[P(X=x) = \frac{1}{\sqrt{2 \pi \sigma}} \exp\left(-\frac{(x-\mu)^2}{2 \sigma^2}\right)\]
  • $\mu$ : 평균
  • $\sigma$ : 표준편차

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=\mu\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big]=\sigma^2\]

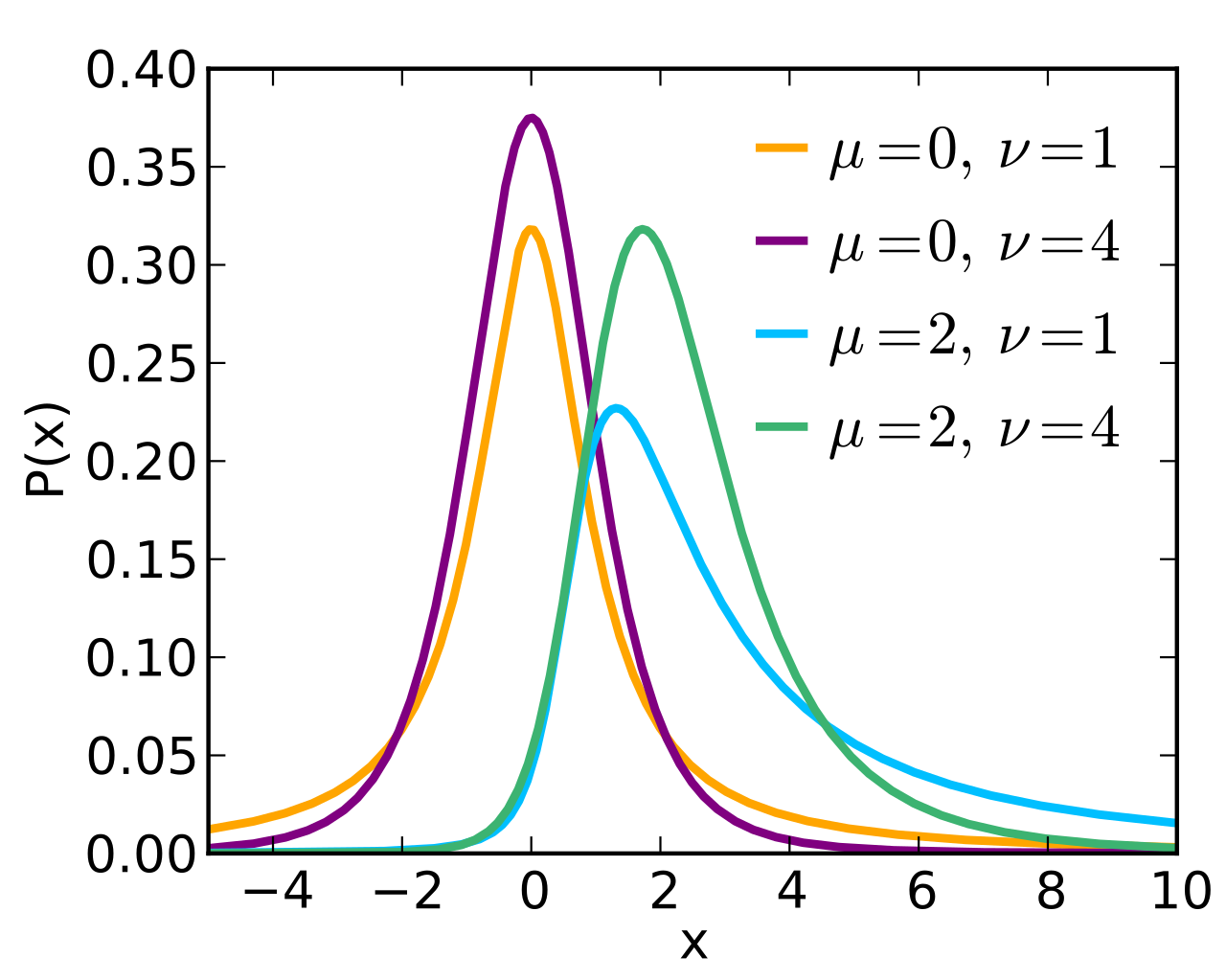
비중심 T-분포(Non-central T-Dist.)

• 정의 : 평균이 $0$ 이 아닌 정규 분포에 기반한 표본 평균의 분포

  \[X \sim t_{\nu}(\delta)\]

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[P(X=x) = \frac{\Gamma\left(\frac{\nu + 1}{2}\right)}{\sqrt{\nu \pi}\Gamma\left(\frac{\nu}{2}\right)}\left(1 + \frac{1}{\nu}\left(\frac{x-\delta}{\sigma}\right)^{2}\right)^{-\frac{\nu+1}{2}}\]
  • $\nu$ : 자유도(Degree of Freedom)
  • $\delta$ : 비중심 매개변수(Non-Centrality Parameter)로서, 분포의 중심
  • $\sigma$ : 스케일 매개변수로서, 표준편차
  • $\Gamma(\cdot)$ : 감마 함수

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big] = \begin{cases}\begin{aligned} &\delta \cdot \frac{\Gamma\left(\frac{\nu-1}{2}\right)}{\sqrt{\frac{\nu}{2}}\Gamma\left(\frac{\nu}{2}\right)} \quad &\text{if}\; \nu > 1\\ &\text{undefined} \quad &\text{if}\; \nu \le 1 \end{aligned}\end{cases}\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big] = \begin{cases}\begin{aligned} &\frac{\nu(1+\delta^2)}{\nu-2}-\left(\delta \cdot \frac{\Gamma\left(\frac{\nu-1}{2}\right)}{\sqrt{\frac{\nu}{2}}\Gamma\left(\frac{\nu}{2}\right)}\right)^2 \quad &\text{if}\; \nu > 2\\ &\infty \quad &\text{if}\; \nu \le 2 \end{aligned}\end{cases}\]

카이제곱 분포(Chi-Squared Dist.)

• 정의 : 표준 정규 분포를 따르는 독립적인 확률변수들의 자승의 합이 특정 값일 확률에 대한 분포

  \[X \sim \chi^{2}(k)\]

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[P(X=x) = \frac{1}{2^{\frac{k}{2}}\cdot \Gamma\left(\frac{k}{2}\right)}x^{\frac{k}{2}-1}\exp(-\frac{x}{2})\]
  • $X$ : 카이제곱 분포를 따르는 확률변수

  • $x > 0$ : $k$ 개의 독립적인 표준 정규 분포 $N(0,1)$ 를 따르는 확률변수 $Z_{i}$ 의 자승의 합

    \[x = \sum_{i=1}^{k}{Z_{i}^{2}} \quad \text{for} \; Z_{i} \sim N(0,1)\]
  • $k$ : 자유도로서 확률변수 $z_{i}$ 의 갯수

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=k\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big]=2k\]

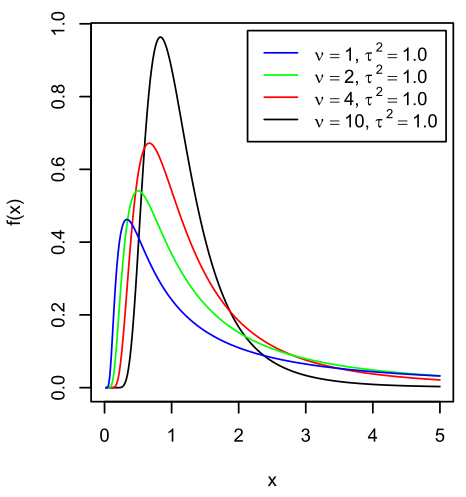
스케일된 역 카이제곱 분포(Scaled Inverse-Chi-Squared Dist.)

• 정의 : 카이제곱 분포의 역수를 따르는 확률 분포

  \[\begin{aligned} X &\sim \chi^{2}(k)\\ \frac{\sigma^2}{X} &\sim \text{Scaled-Inv-}\chi^{2}(k,\sigma^2) \end{aligned}\]

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[P(Y=y) = \frac{1}{\Gamma\left(\frac{k}{2}\right)}\left(\frac{k}{2\sigma^2}\right)^{\frac{k}{2}}y^{-\frac{k}{2}-1}\exp\left(-\frac{k}{2\sigma^2y}\right)\]
  • $Y=\displaystyle\frac{\sigma^2}{X}$ : 스케일된 역카이제곱 분포를 따르는 확률변수
  • $y > 0$
  • $k$ : 자유도
  • $\sigma^2$ : 스케일 매개변수
  • $\Gamma(\cdot)$ : 감마 함수

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=\frac{k \cdot \sigma^2}{k-2} \quad \text{s.t.}\; k>2\]

• 분산(Variance)

  \[\mathbb{V}\big[X\big]=\frac{2 \cdot k^2 \cdot \sigma^4}{(k-2)^2(k-4)} \quad \text{s.t.}\; k>4\]

위샤트 분포(Wishart Dist.)

• 정의 : 양정치 행렬(Positive Definite Matrix)에 대한 확률 분포

  \[X \sim W_{p}(\mathbf{V},n)\]
  • 다변량 정규 분포(Multi-variat Normal Distribution) $N(\mu, \Sigma)$ 의 공분산 행렬 $\Sigma$ 에 대한 사전확률분포

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[\begin{aligned} P(X=\mathbf{X}) &= \frac{1}{2^{\frac{np}{2}} \vert \mathbf{V} \vert ^{\frac{n}{2}}\Gamma_{p}(\frac{n}{2})} \vert \mathbf{X} \vert ^{\frac{n-p-1}{2}}\exp\left(-\frac{1}{2}\text{tr}(\mathbf{V}^{-1}\mathbf{X})\right)\\ \Gamma_{p}\left(\displaystyle\frac{n}{2}\right) &=\pi^{\frac{p(p-1)}{4}}\prod_{i=1}^{p}{\Gamma\left(\displaystyle\frac{n-(i-1)}{2}\right)}\\ \text{tr}(\mathbf{V}^{-1}\mathbf{X}) &=\sum_{i}{(\mathbf{V}^{-1}\mathbf{X})_{ii}} \end{aligned}\]
  • $X$ : 위샤트 분포를 따른 확률변수
  • \(\mathbf{X}=\sum_{i=1}^{n}{\overrightarrow{z}_{i} \cdot \overrightarrow{z}_{i}^{T}}\) : $p \times p$ 양정치 행렬(Positive Definite Matrix)
    • 표준 정규 분포 \(N(0,1)\) 를 따르는 \(p\) 차원 벡터 \(\overrightarrow{z}_{1},\overrightarrow{z}_{2},\cdots,\overrightarrow{z}_{n}\) 생성
    • 외적 \(\overrightarrow{z}_{i} \cdot \overrightarrow{z}_{i}^{T}\) 을 통해 \(p \times p\) 양정치 행렬 \(n\) 개 생성
    • $n$ 개의 $p \times p$ 양정치 행렬을 덧셈하여 $\mathbf{X}$ 생성
  • $n>p-1$ : 자유도로서 $\overrightarrow{z}_{i} \sim N(0,1)$ 갯수

  • $\mathbf{V}>0$ : 양정치 행렬로서, 벡터 $\overrightarrow{z}_{i} \sim N(0,1)$ 간 공분산을 조정함으로써 분포의 형태와 스케일을 결정

  • $\Gamma(\cdot)$ : 감마 함수

• 기대값(Expected Value)

  \[\mathbb{E}\big[X\big]=n \cdot \mathbf{V}\]

• 분산(Variance)

  \[\mathbb{V}\big[X_{ij}\big]=n(\mathbf{V}_{ij}^{2}+\mathbf{V}_{ii}\mathbf{V}_{jj})\]

디리클레 분포(Dirichlet Dist.)

• 정의 : 베타분포의 다변수 확장으로서, 여러 카테고리의 비율에 대한 확률 분포

  \[X \sim \text{Dirichlet}(\alpha_{1}, \cdots, \alpha_{k})\]
  • 각 정당에 대한 투표 비율이 특정 값일 확률에 대한 분포

• 확률 밀도 함수(Prob. Density Function, PDF)

  \[P(X_1=x_1, \cdots, X_k=x_k) = \frac{\Gamma(\alpha_{1}+\cdots+\alpha_{k})}{\Gamma(\alpha_{1}) \cdots \Gamma(\alpha_{k})}x_{1}^{\alpha_{1}-1} \cdots x_{k}^{\alpha_{k}-1}\]
  • $0 \le x_{i} \le 1$ : 전체 카테고리 대비 $i$ 번째 카테고리가 차지하는 비중
  • $\alpha_{i}$ : $i$ 번째 카테고리의 강도
  • $\Gamma(\cdot)$ : 감마 함수

• 기대값(Expected Value)

  \[\mathbb{E}\big[X_{i}\big]=\frac{\alpha_{i}}{\sum_{i}{\alpha_{i}}}\]

• 분산(Variance)

  \[\mathbb{V}\big[X_{i}\big]=\frac{\alpha_{i}(\sum_{i}{\alpha_{i}}-\alpha_{i})}{\left(\sum_{i}{\alpha_{i}}\right)^{2}(\sum_{i}{\alpha_{i}}+1)}\]

• 공분산(Covariance)

  \[\mathbb{V}\big[X_{i},X_{j}\big]=-\frac{\alpha_{i} \cdot \alpha_{j}}{\left(\sum_{i}{\alpha_{i}}\right)^{2}(\sum_{i}{\alpha_{i}}+1)}\]