Producer Theory (1) Output Maximization under Cost Constraint

Production

---

• 개별생산자의 최적 의사결정 과정

  • 이윤을 극대화하는 생산량 수준 $Q^{*}_{S}$ 도출

    \[Q^{*}_{S} = \text{arg} \max{\pi}\]

  • 이윤 극대화 생산량 $Q^{*}_{S}$ 을 최소 비용으로 달성하는 요소조합 $\left(\hat{L}, \hat{K}\right)$ 도출

    \[\hat{L}, \hat{K}=\text{arg} \min{L \cdot w + K \cdot v} \quad \text{s.t.} \; Q^{*}_{S}=F(L,K)\]

Production

• 생산 함수(Production Function) : 단기 콥-더글라스 생산 함수임을 가정

  가정 : 생산 기간은 단기로 간주하고, 투입되는 생산요소를 노동($L$)과 자본($K$)으로 제한하자. 단기에는 고정투입요소의 투입량을 유동적으로 조정할 수 없으며($\overline{K}$), 생산기술이 일정한 수준으로 유지된다($\overline{H}$).

  \[\begin{aligned} Q_S &= F\left(L,\overline{K}\right)\\ &= \overline{H} \cdot L^{\alpha} \cdot \overline{K}^{\beta} \end{aligned}\]
  • $Q_S$ : 개별생산량
  • $L$ : 노동으로서 가변투입요소
  • $\overline{K}$ : 자본으로서 고정투입요소
  • $\overline{H}$ : 생산기술

• 등량 곡선(Isoquant Curve) : 노동 투입량을 X축으로, 자본 투입량을 Y축으로 하는 좌표평면 위에 생산량이 무차별한 요소조합을 이은 곡선

  

  \[Q_K = F(L, K)\]
  1. 동일한 생산함수의 상이한 생산량수준을 나타내는 두 개의 등량곡선은 교차하지 않는다.
  2. 원점에서 비교적 먼 등량곡선은 비교적 높은 생산량수준을 나타낸다.
  3. 등량곡선은 우하향한다.
  4. 제1사분면 위에 존재하는 임의의 점에 대하여 그 점을 지나는 등량곡선이 하나 존재한다.
  5. 등량곡선은 원점에 대하여 볼록한 모양을 가진다.

Productivity of Factors of Production

• 생산요소의 생산력

  

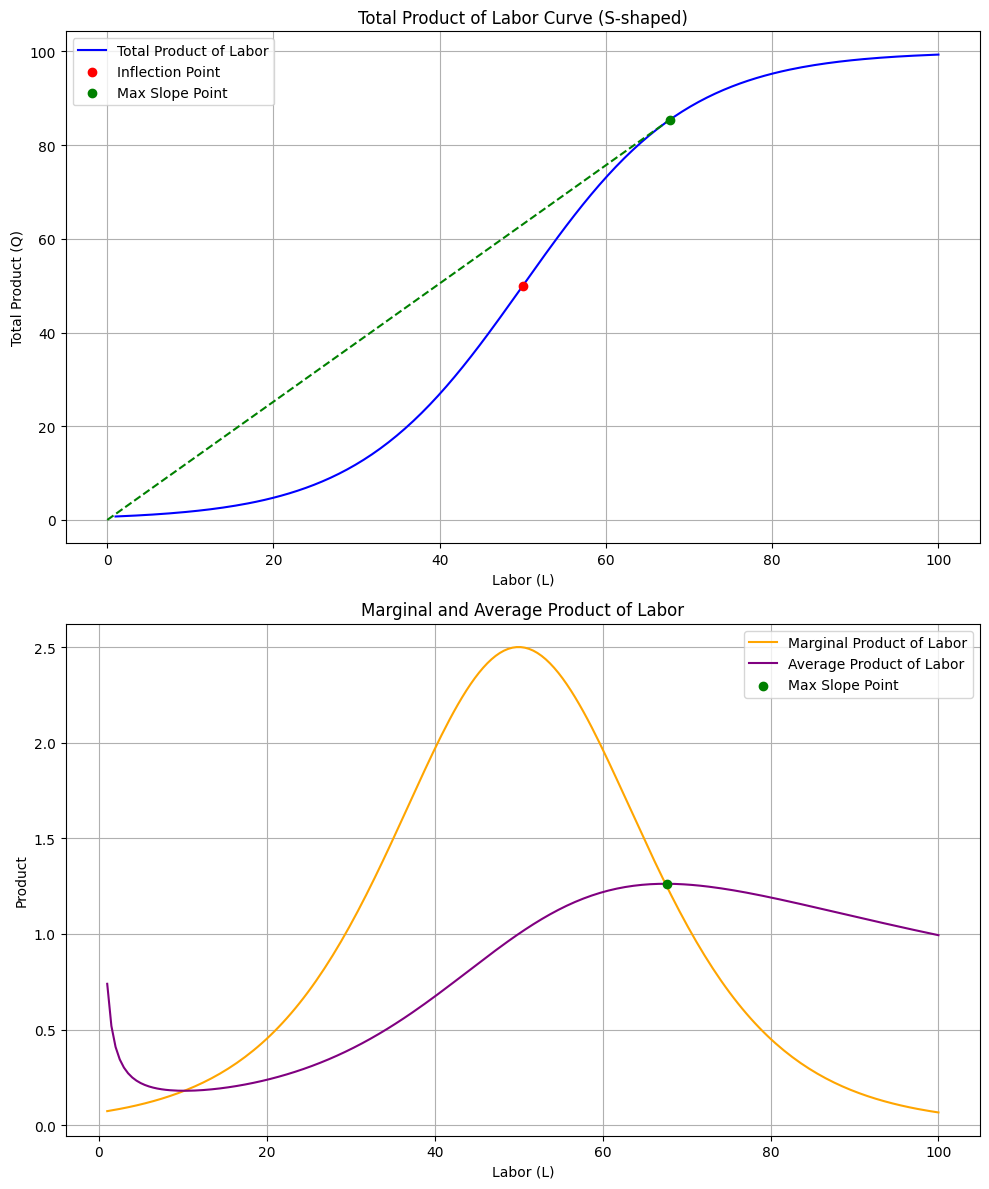
  • 노동의 총생산(Total Production of Labor; $TP_L$) : 노동을 $L$ 단위 투입했을 때 가능한 생산량

    \[TP_L = f(L,\overline{K})\]

  • 노동의 평균생산(Average Production of Labor; $AP_L$) : 노동 단위당 가능한 생산량

    \[AP_L = \frac{TP_L}{L}\]

  • 노동의 한계생산(Marginal Production of Labor; $MP_L$) : 노동 단위 추가 투입 시 가능한 추가 생산량

    \[MP_L = \frac{\partial TP_L}{\partial L}\]

• 한계기술대체율(Marginal Rate of Technical Substitution; MRTS) : 동일한 생산량 수준에서 특정 생산요소를 한 단위 추가 투입하기 위해 포기해야 하는 다른 생산요소 단위

  \[\Delta L \cdot MP_L + \Delta K \cdot MP_K = 0\] \[\therefore MRTS_{L,K}:= -\frac{\Delta K}{\Delta L} = \frac{MP_L}{MP_K}\]

• 한계기술대체율 체감의 법칙 : 특정 생산요소의 투입량이 증가할수록 동일한 생산량 수준에서 해당 생산요소를 한 단위 추가 투입하기 위해 포기해야 하는 다른 생산요소의 투입분이 감소하는 현상

  \[\frac{\partial MRTS_{L,K}}{\partial L} \prec 0\]

Cost Constraint

---

• 등비용곡선(Iso-Cost Curve) : 주어진 비용($C$)과 요소가격 상황($P_L=w,P_K=v$)에 맞게 취득할 수 있는 요소조합의 집합

  \[(L,K) \quad \text{s.t.} \; L \cdot w + K \cdot v \le C\]

• 상대가격(Relative Price) : 특정 생산요소에 대하여, 동일한 비용 수준에서 해당 생산요소를 한 단위 추가 투입하기 위해 포기해야 하는 다른 생산요소의 투입분

  \[\Delta L \cdot w + \Delta K \cdot v = 0\] \[\therefore - \frac{\Delta K}{\Delta L} = \frac{w}{v}\]

Output Maximization under Cost Constraint

---

\[\max{Q_S} \quad \text{s.t.} \; x \cdot P_{X} + y \cdot P_{Y} \le M\]

• 등량곡선의 접선의 기울기 : 노동의 자본에 대한 한계기술대체율 $MRTS_{L,K}$

  \[-\frac{\Delta K}{\Delta L} = \frac{MP_L}{MP_K}\]

• 등비용곡선의 기울기 : 노동의 자본에 대한 상대가격

  \[-\frac{\Delta K}{\Delta L} = \frac{w}{v}\]

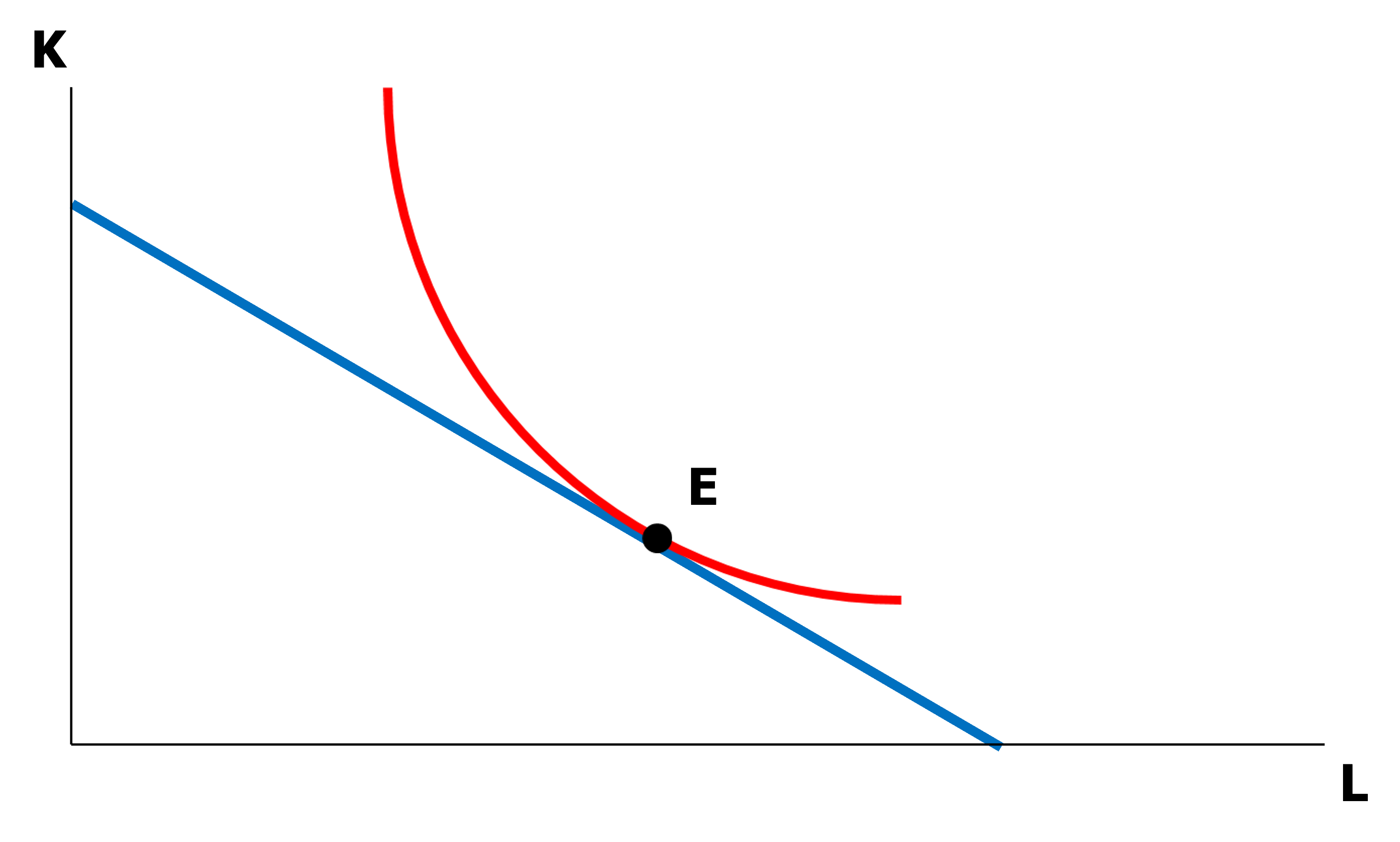
• 등비용곡선과 등량곡선의 접점 : 비용 제약 하 생산량을 극대화하는 요소조합

  \[\begin{aligned} \frac{MP_L}{MP_K}=-\frac{\Delta K}{\Delta L}=\frac{w}{v} \end{aligned}\]

• 최적 선택 하에서는 $\displaystyle\frac{MP_{L}}{w}$ 과 $\displaystyle\frac{MP_{K}}{v}$ 이 일치함

  \[\frac{MP_{L}}{MP_{K}}=\frac{w}{v} \Leftrightarrow \frac{MP_{L}}{w}=\frac{MP_{K}}{v}\]
  • $\displaystyle\frac{MP_{L}}{w}$ : 화폐 단위당 취득 가능한 노동 단위의 한계생산
  • $\displaystyle\frac{MP_{K}}{v}$ : 화폐 단위당 취득 가능한 자본 단위의 한계생산