Producer Theory (2) Profit Maximization

Revenue

---

• 총수익(Total Revenue; TR) : 개별생산자가 재화를 공급하고서 취득할 수 있는 수익의 총합

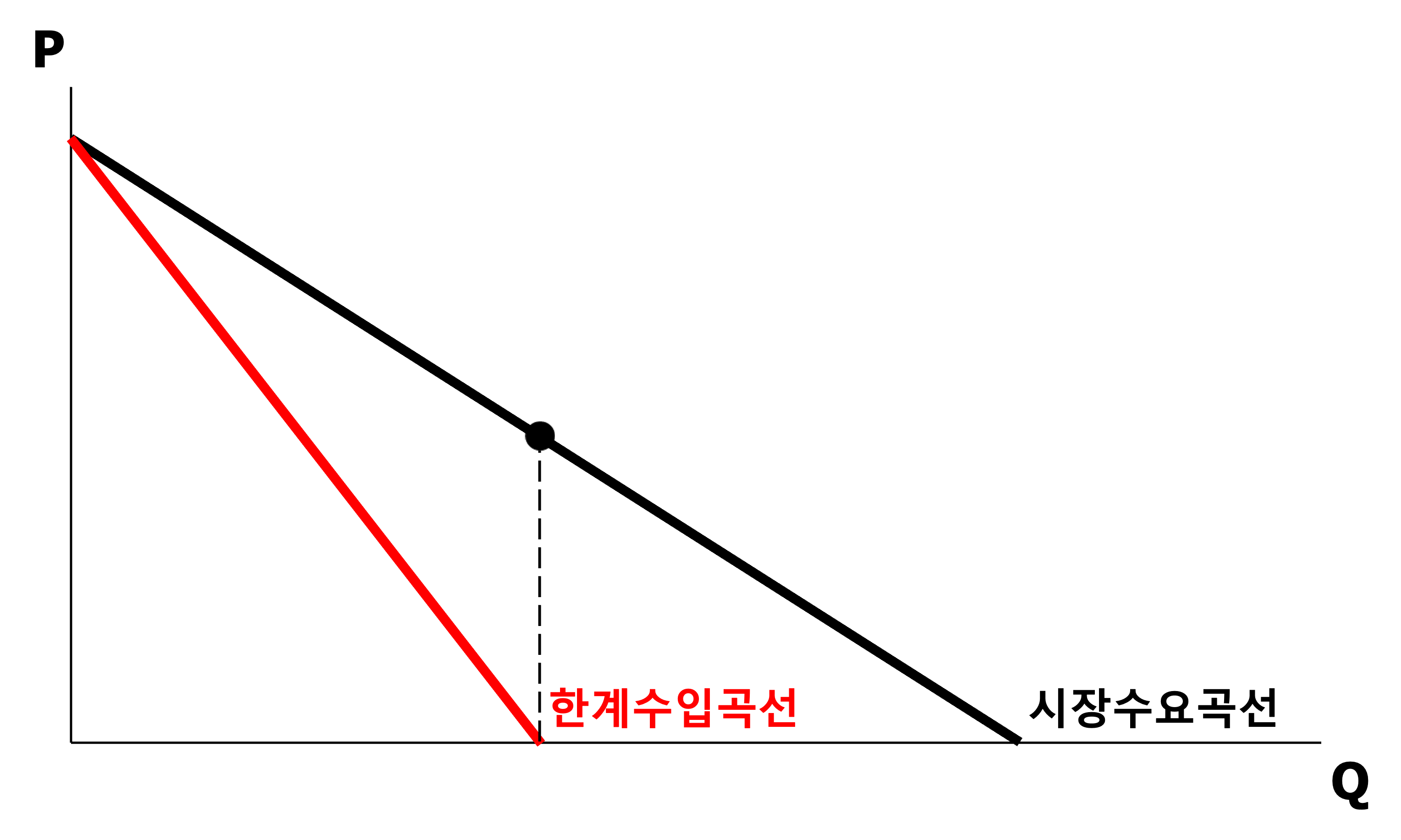
  \[\begin{aligned} TR(Q \vert \alpha, \beta) &=P \cdot Q\\ &=\left(\alpha - \beta \cdot Q \right) \cdot Q \end{aligned}\]
  • $P=\alpha - \beta \cdot Q$ : 단위당 시장가격
  • $Q$ : 총 공급량

• 평균수익(Average Revenue; AR) : 개별생산자가 재화 단위당 취득할 수 있는 수익

  \[\begin{aligned} AR(Q \vert \alpha, \beta) &= \frac{TR(Q \vert \alpha, \beta)}{Q}\\ &= P \end{aligned}\]

• 한계수익(Marginal Revenue; MR) : 개별생산자가 재화를 한 단위 추가 공급했을 때 추가 취득할 수 있는 수익

  \[\begin{aligned} MR(Q \vert \alpha, \beta) &= \frac{\partial TR(Q \vert \alpha, \beta)}{\partial Q}\\ &= \alpha - 2 \beta \cdot Q \end{aligned}\]

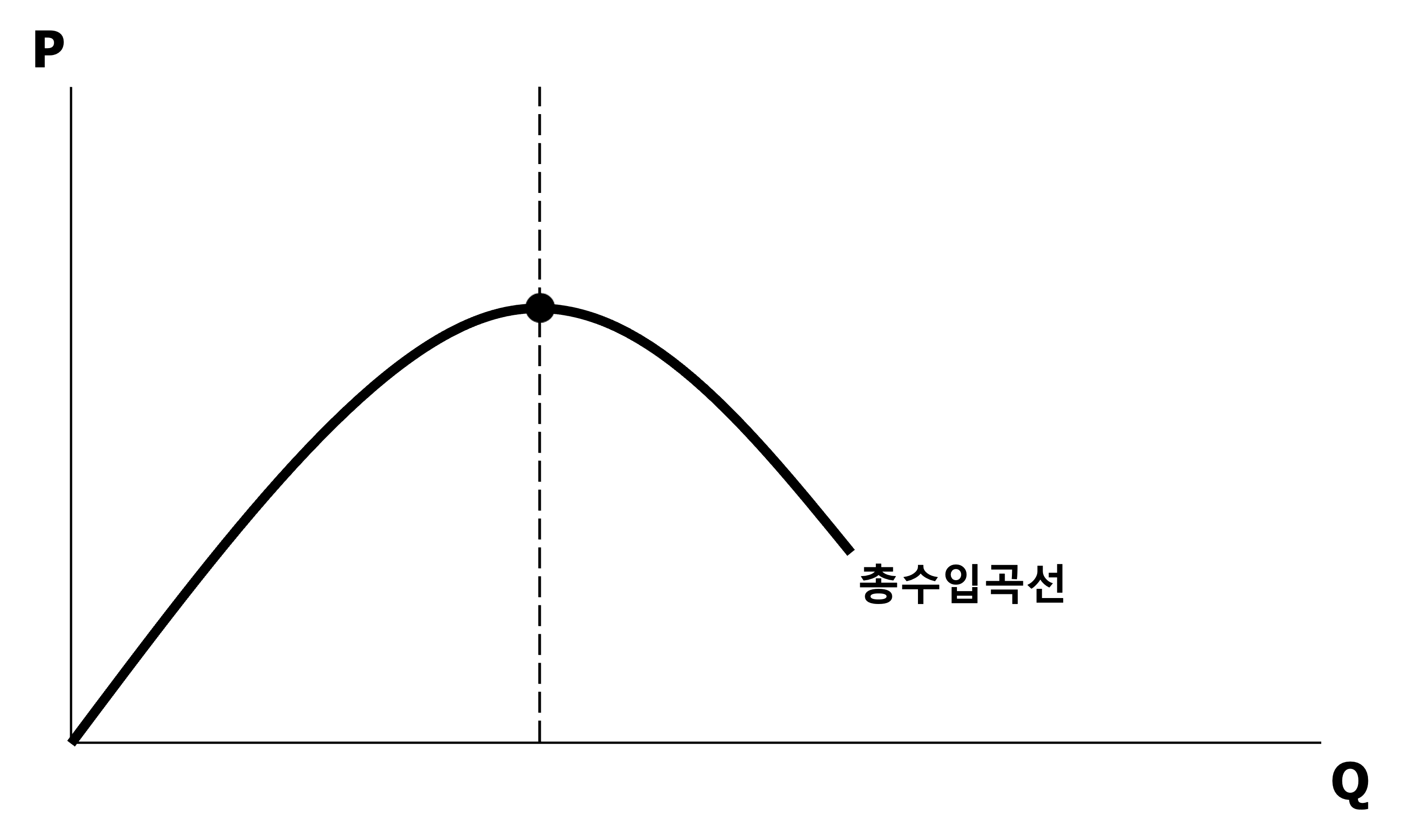
$\max{TR}$

\[\begin{aligned} \frac{\partial TR(Q \vert \alpha, \beta)}{\partial Q} &= MR(Q)\\ &= P \cdot \left(1 + \frac{Q / \Delta Q}{P / \Delta P}\right)\\ &= P \cdot \left(1 - \frac{1}{\varepsilon_{P}} \right)\\ &= 0 \end{aligned}\]

\[\therefore \hat{Q} = \text{arg}\max{TR(Q \vert \alpha, \beta)} \quad \text{for} \; \varepsilon_{P}=1\]

Cost

---

Short-Term Cost

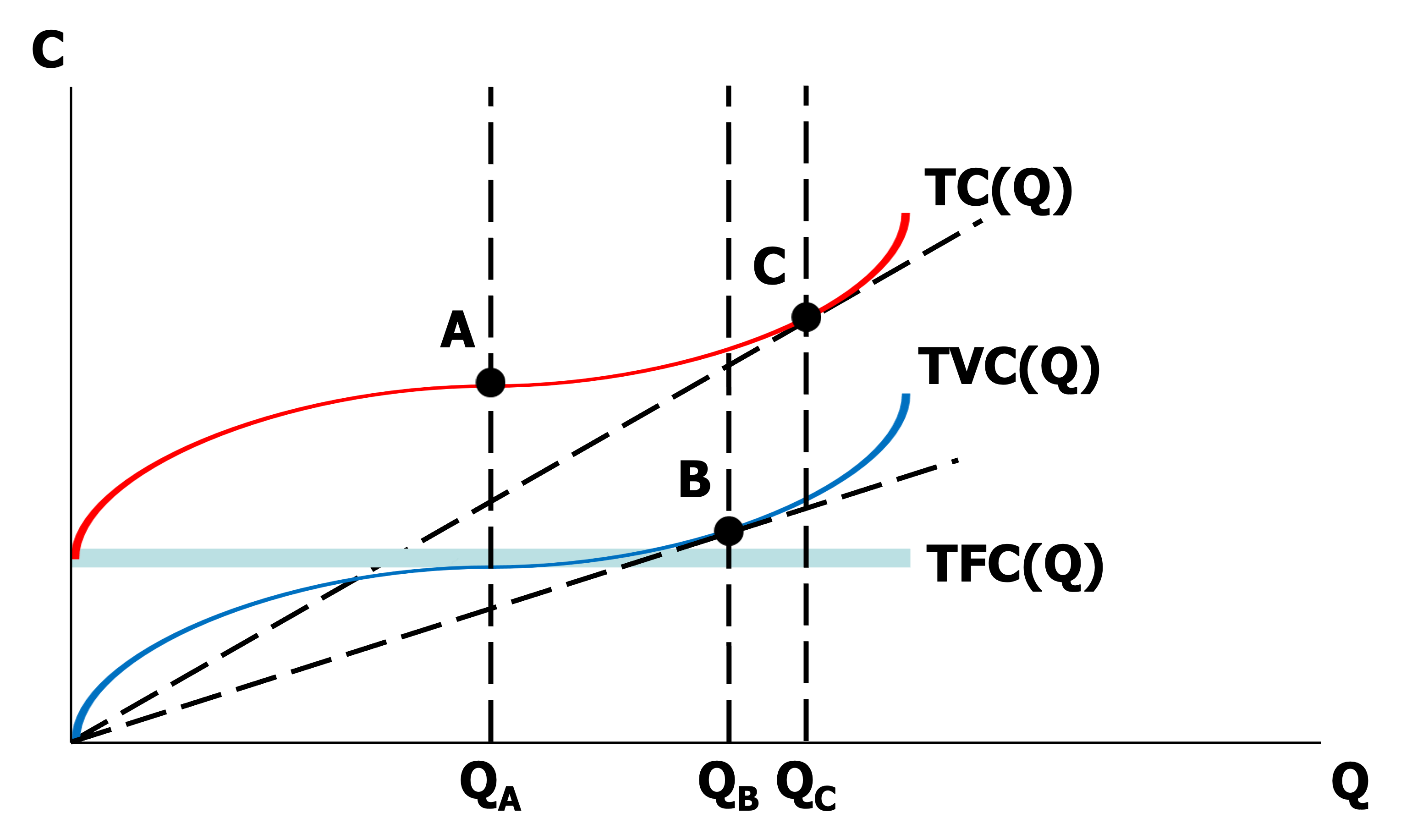
• 단기총비용(Short-Term Total Cost; STC) : 개별생산자가 재화를 총 $Q$ 단위 공급하기 위해 지불해야 하는 비용

  \[\begin{aligned} STC(Q \vert K) &= STVC(Q) + STFC\\ STVC(Q) &= L \cdot w\\ STFC &= \overline{K} \cdot v \end{aligned}\]

• 단기평균비용(Short-Term Average Cost; SAC) : 개별생산자가 재화 단위당 지불해야 하는 비용

  \[\begin{aligned} SAC(Q \vert K) &= \frac{STC(Q \vert K)}{Q}\\ &= \frac{STVC(Q)}{Q} + \frac{STFC}{Q} \end{aligned}\]

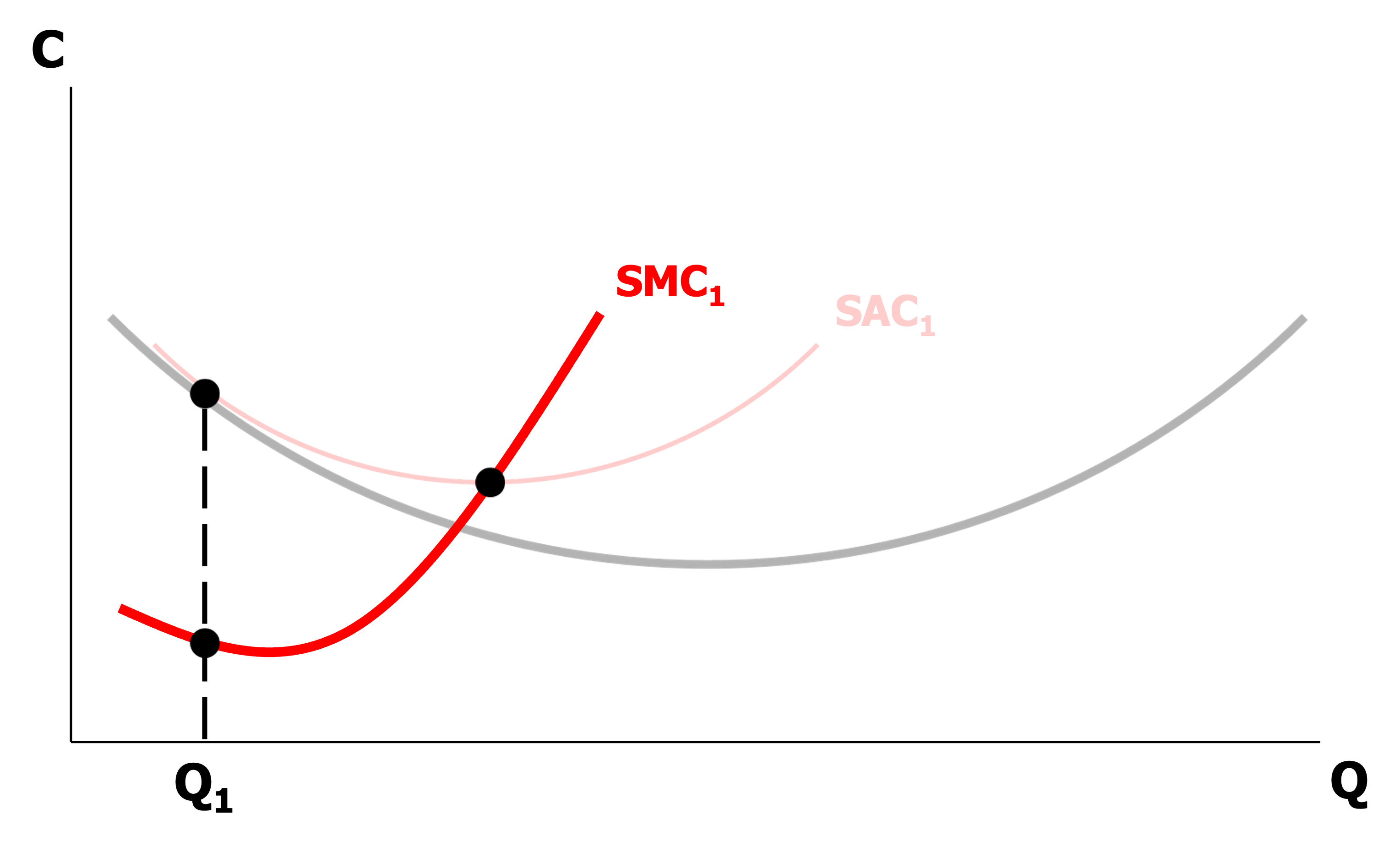
• 단기한계비용(Short-Term Marginal Cost; SMC) : 개별생산자가 재화 단위를 추가할 때 추가 지불해야 하는 비용

  \[\begin{aligned} SMC(Q \vert K) &= \frac{\partial STC(Q \vert K)}{\partial Q}\\ &= \frac{\partial STVC(Q)}{\partial Q} + \frac{\partial STFC}{\partial Q}\\ &= \frac{\partial STVC(Q)}{\partial Q} \quad \left(\because \frac{\partial STFC}{\partial Q} = 0 \right) \end{aligned}\]

Long-Term Cost

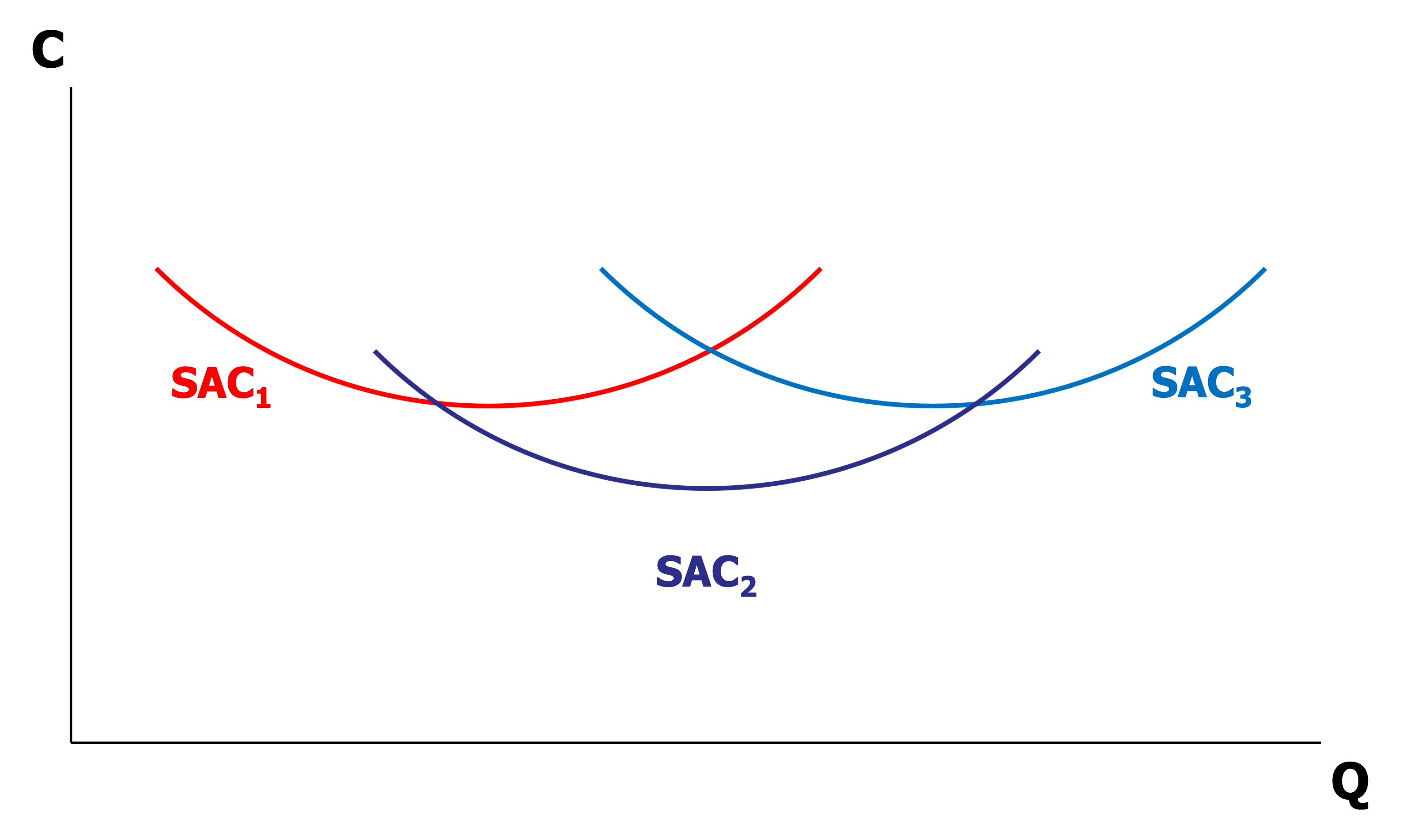
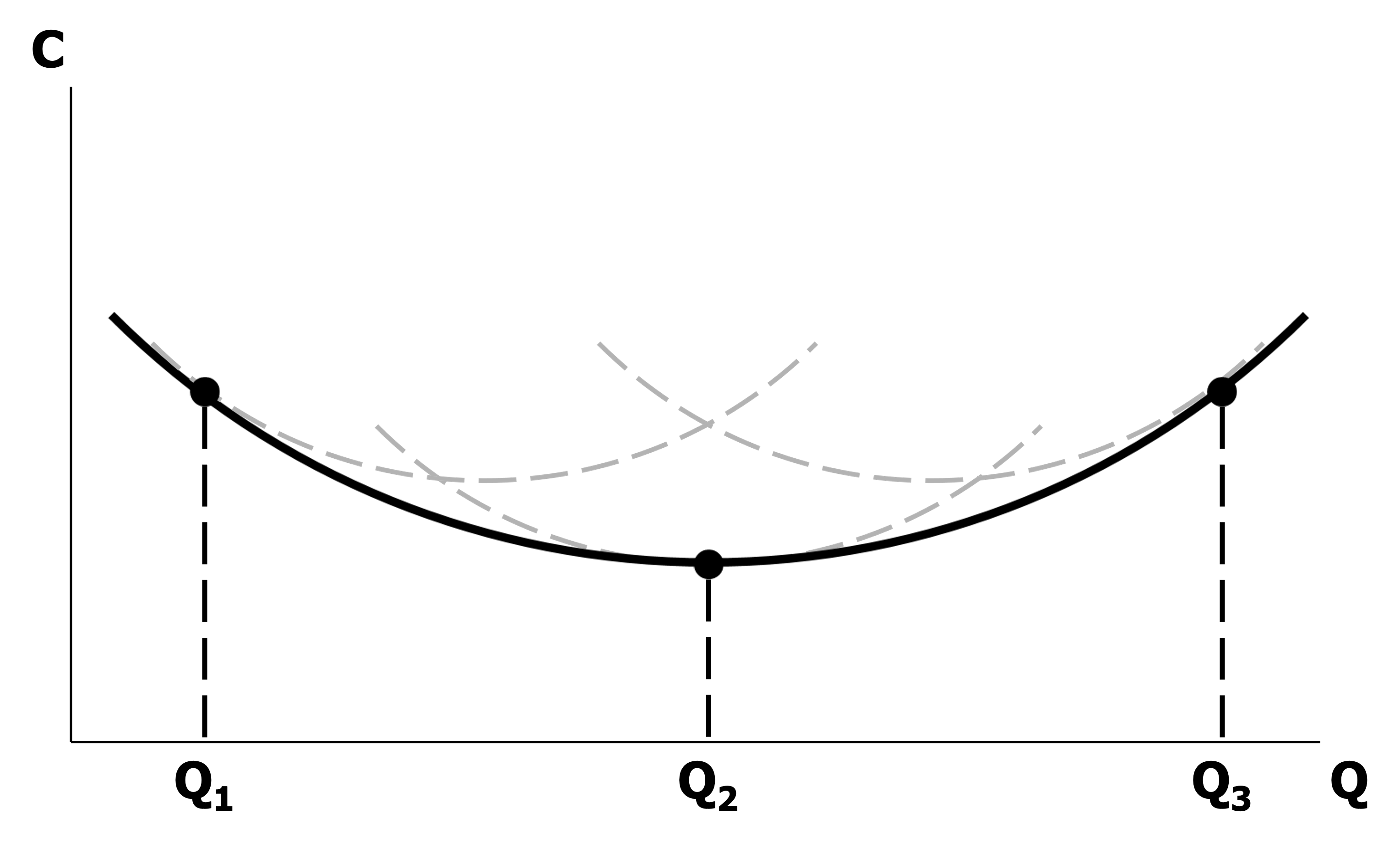
• 장기평균비용(Long-Term Average Cost; LAC) : 각 생산량 수준($Q$)에서 단기평균비용이 최저인 점들의 집합

  

  \[LAC(Q)=\min_{K}{SAC(Q \vert K)}\]

• 장기한계비용(Long-Term Marginal Cost; LMC) : 각 생산량 수준($Q$)에서 채택된 단기평균비용곡선에 대응하는 단기한계비용곡선 점들의 집합

  

  \[\begin{aligned} LMC(Q)&= SMC\left(Q \vert \hat{K} \right)\\ \hat{K}&= \text{arg} \min_{K}{SAC\left(Q \vert K \right)} \end{aligned}\]

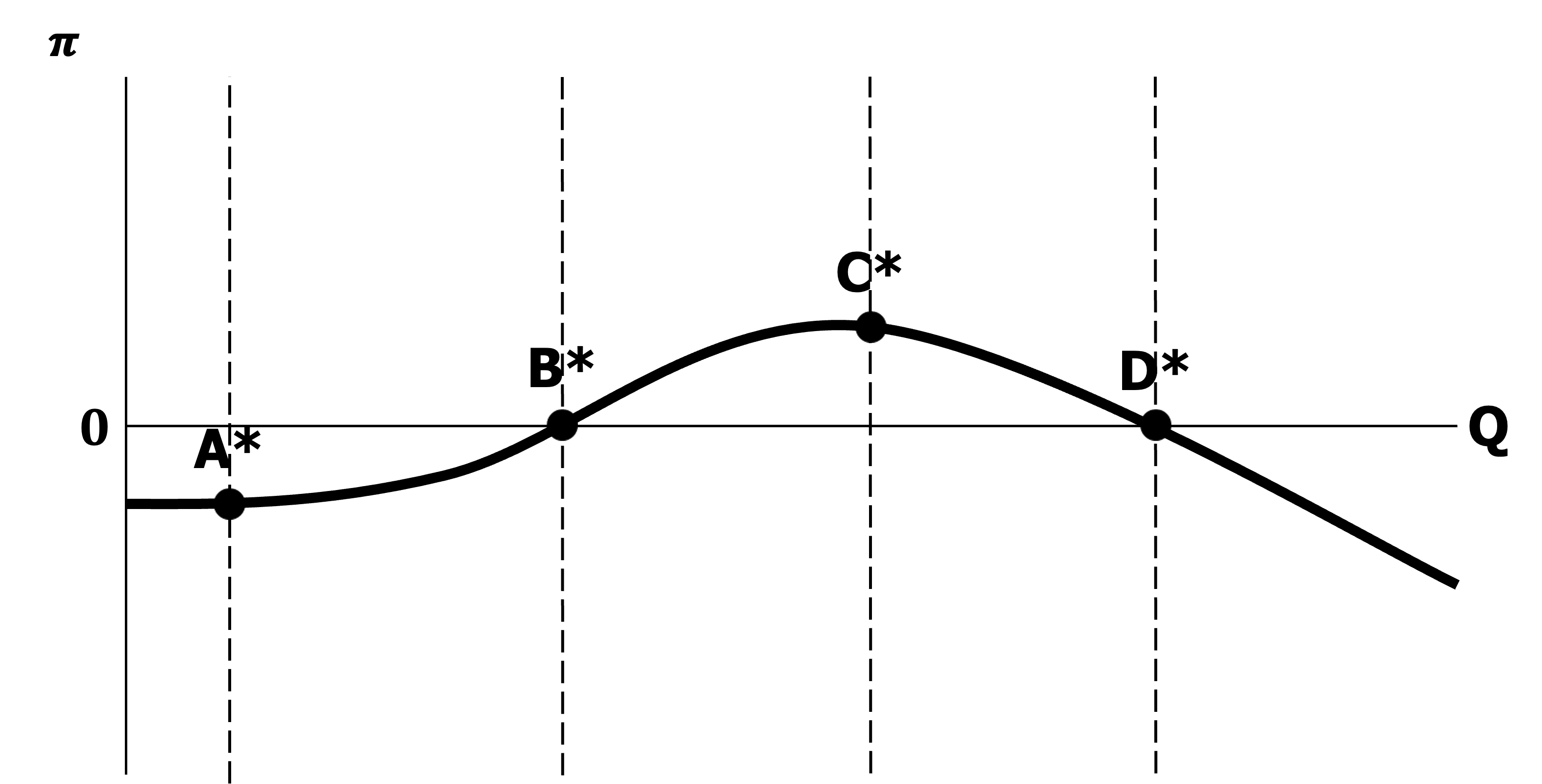
Profit Maximization

---

• 양의 이윤을 극대화하는 생산량 도출

  \[Q_{S}^{*}= \text{arg} \max{\pi(Q)}\]

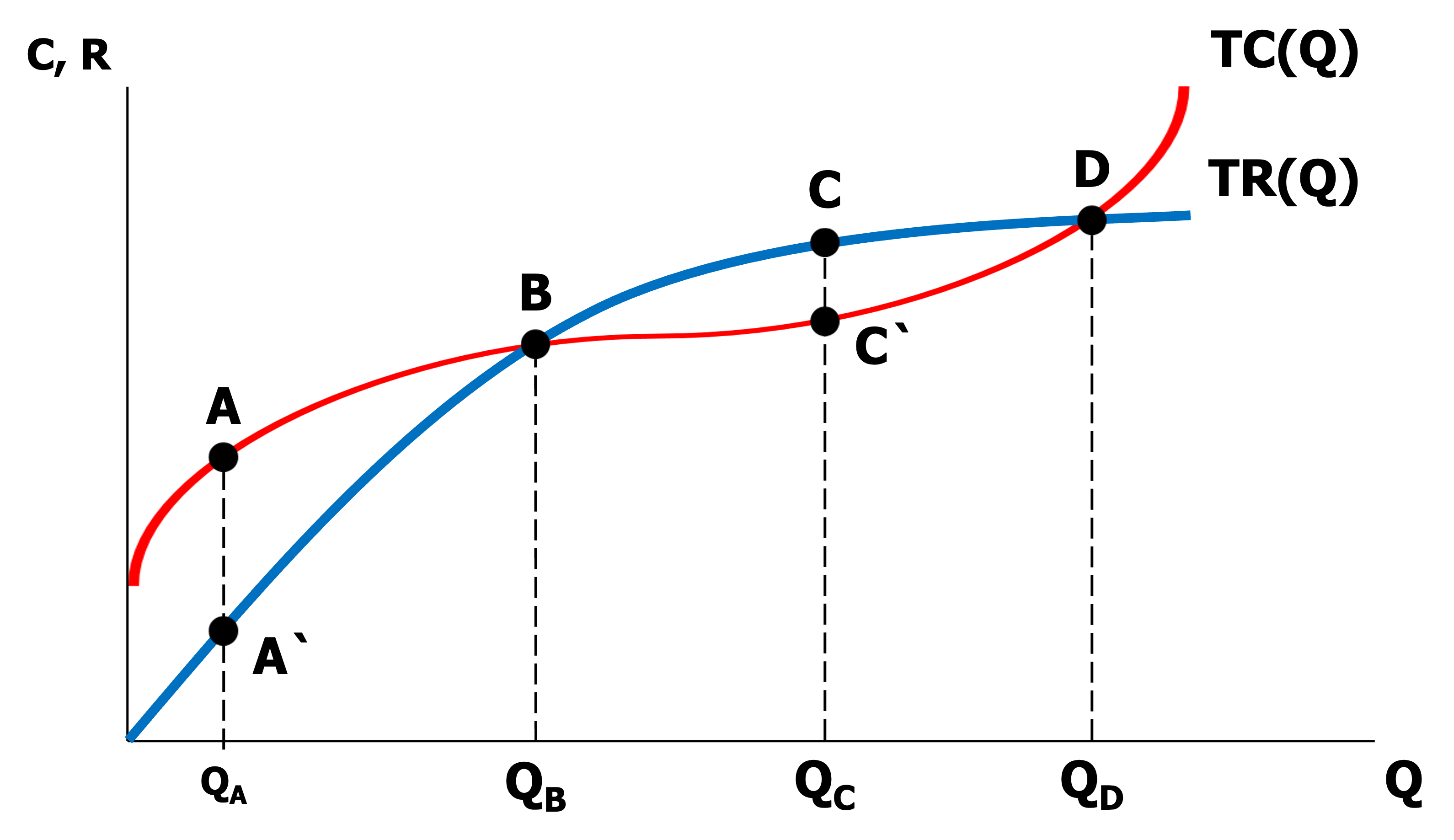
• 이윤 함수(Profit Function)

  \[\pi(Q) = TR(Q) - TC(Q)\]

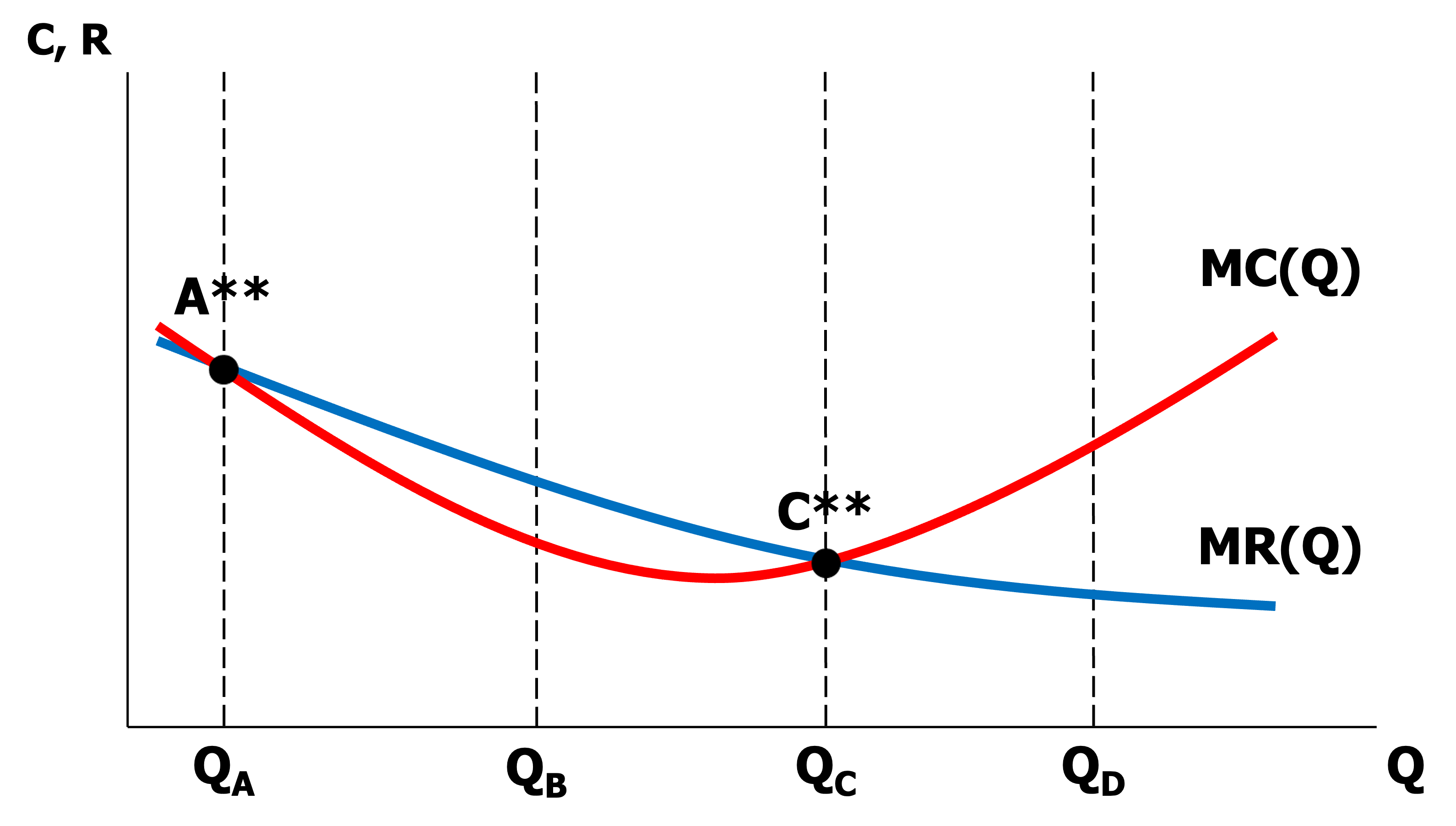
• 일계 조건

  \[\begin{aligned} \frac{\partial \pi(Q)}{\partial Q} &= \frac{\partial TR(Q)}{\partial Q} - \frac{\partial TC(Q)}{\partial Q}\\ &= MR(Q) - MC(Q)\\ &=0\\\\ \therefore MR(Q)&=MC(Q) \end{aligned}\]

• 이계 조건

  \[\begin{aligned} \frac{\partial^2 \pi(Q)}{\partial Q^2} &= \frac{\partial}{\partial Q} \frac{\partial \pi(Q)}{\partial Q}\\ &= \frac{\partial MR(Q)}{\partial Q} - \frac{\partial MC(Q)}{\partial Q}\\ &< 0\\\\ \therefore \frac{\partial MR(Q)}{\partial Q} &< \frac{\partial MC(Q)}{\partial Q} \end{aligned}\]