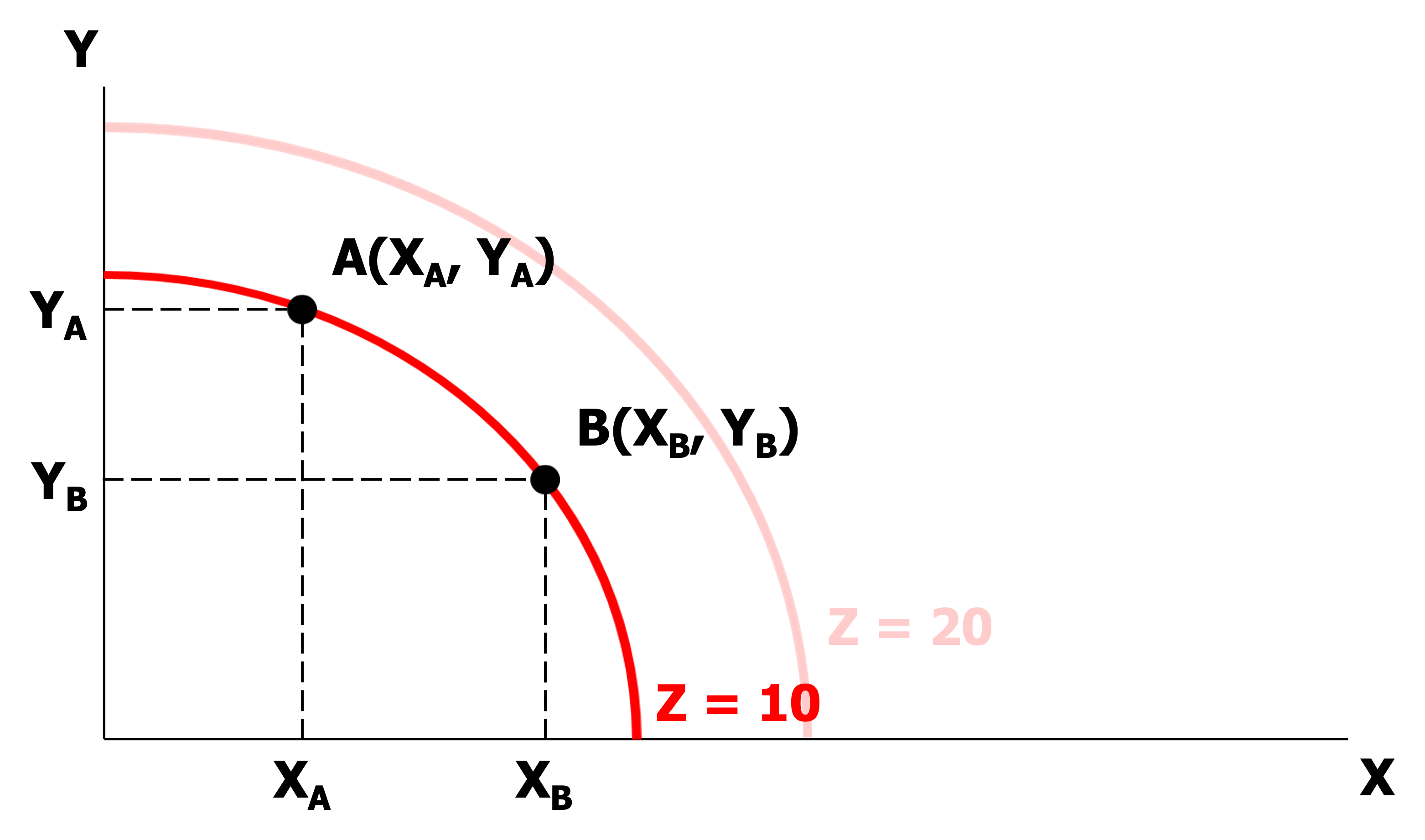Producer Theory (3) Joint Production

Joint Production

---

• 결합 생산(Joint Production) : 개별생산자가 두 가지 품종 이상을 함께 생산하는 경우

  \[Z = F(X,Y)\]

• 생산변환곡선(Product Transformation Curve) : 재화 $X,Y$ 에 대하여, 생산하는데 동일한 비용($Z$)이 요구되는 상품묶음 $(X,Y)$ 의 집합

  

• 한계생산변환율(Marginal Rate of Product Transformation; MRPT) : 재화 $X,Y$ 에 대하여, 동일한 비용 수준에서 특정 재화를 한 단위 추가 생산하기 위해 포기해야 하는 다른 재화의 공급분

  \[\Delta x \cdot MC_X + \Delta y \cdot MC_Y = 0\] \[\therefore MRPT_{X,Y}:= -\frac{\Delta y}{\Delta x} = \frac{MC_X}{MC_Y}\]
  • $MC_X = \displaystyle\frac{\partial z}{\partial x}$ : 재화 $X$ 에 대한 한계비용
  • $MC_Y = \displaystyle\frac{\partial z}{\partial y}$ : 재화 $Y$ 에 대한 한계비용

• 한계생산변환율 체증의 법칙 : 특정 재화의 생산량이 증가할수록 동일한 비용 수준에서 해당 재화를 한 단위 추가 생산하기 위해 포기해야 하는 다른 재화의 공급분이 증가하는 현상

  \[\frac{\partial MRPT_{X,Y}}{\partial X} \succ 0\]

Revenue Constraint

---

• 한계수익불변 하 등수익곡선(Iso-Revenue Curve subject to Constant Marginal Revenue) : 공급 시 동일한 수익을 얻을 수 있는 상품묶음의 조합

  \[X \cdot P_X + Y \cdot P_Y \le R\]

  • 한계수익불변(Constant Marginal Revenue) : 한계수익이 특정 재화의 공급량 변화에 반응하지 아니하고 일정함

    \[\frac{\partial R}{\partial X}=\overline{\alpha},\frac{\partial R}{\partial Y}=\overline{\beta}\]

• 상대가격(Relative Price) : 재화 $X,Y$ 에 대하여, 동일한 수익 수준에서 특정 재화를 한 단위 추가 공급하기 위해 포기해야 하는 다른 재화의 공급분

  \[\Delta X \cdot P_{X} + \Delta Y \cdot P_{Y} = 0\] \[\therefore - \frac{\Delta Y}{\Delta X} = \frac{P_{X}}{P_{Y}}\]

Cost Minimization under Revenue Constraint

---

\[\min{Z} \quad \text{s.t.} \; X \cdot P_{X} + Y \cdot P_{Y} \le R\]

• 생산변환곡선의 접선의 기울기 : 재화 $X,Y$ 에 대하여, $X$ 의 $Y$ 에 대한 한계생산변환율 $MRPT_{X,Y}$

  \[-\frac{\Delta Y}{\Delta X} = \frac{MC_X}{MC_Y}\]

• 등수익곡선의 기울기 : 재화 $X,Y$ 에 대하여, $X$ 의 $Y$ 에 대한 상대가격

  \[-\frac{\Delta Y}{\Delta X} = \frac{P_X}{P_Y}\]

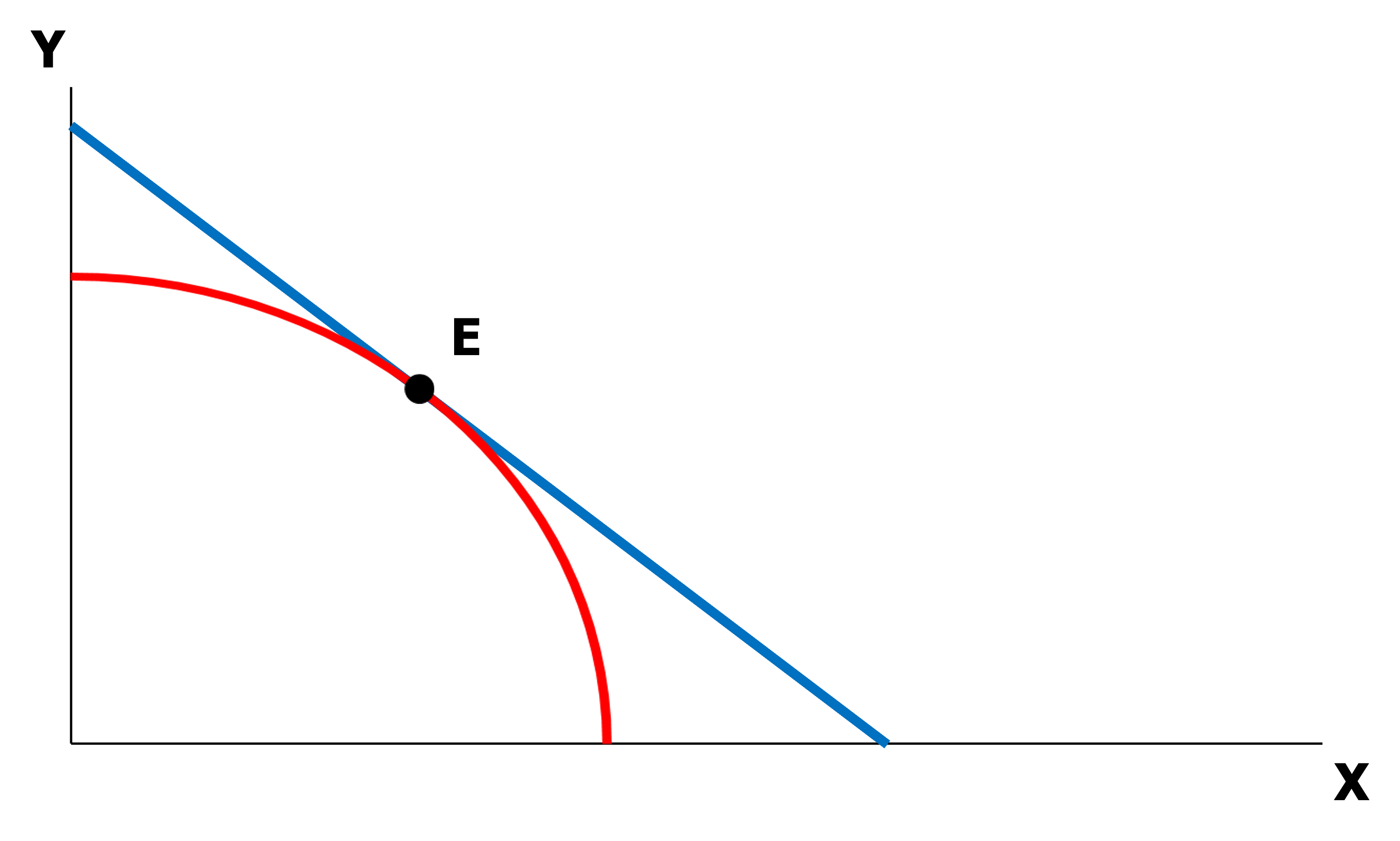
• 생산변환곡선과 등수익곡선의 접점 : 수익 제약 하 비용을 최소화하는 상품묶음

  \[\begin{aligned} \frac{MC_X}{MC_Y}=-\frac{\Delta Y}{\Delta X}=\frac{P_X}{P_Y} \end{aligned}\]

• 최적 선택 하에서는 $\displaystyle\frac{MC_{X}}{P_X}$ 와 $\displaystyle\frac{MC_{Y}}{P_Y}$ 가 일치함

  \[\frac{MC_{X}}{MC_{Y}}=\frac{P_X}{P_Y} \Leftrightarrow \frac{MC_{X}}{P_X}=\frac{MC_{Y}}{P_Y}\]
  • $\displaystyle\frac{MC_{X}}{P_X}$ : 화폐 단위당 취득 가능한 $X$ 단위의 한계비용
  • $\displaystyle\frac{MC_{Y}}{P_Y}$ : 화폐 단위당 취득 가능한 $Y$ 단위의 한계비용