Recurrent Neural Networks

Why? Recurrent-Net

---

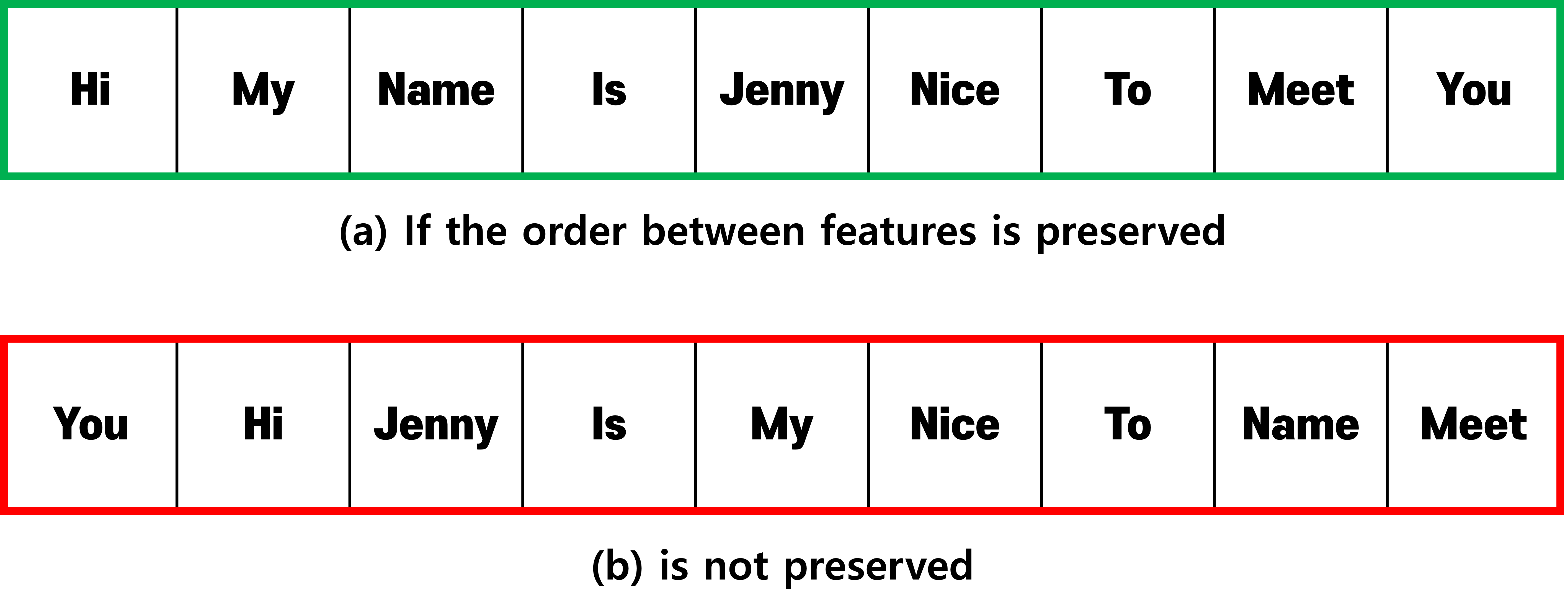
• Time series data is data
  where there is a sequence between features:

  

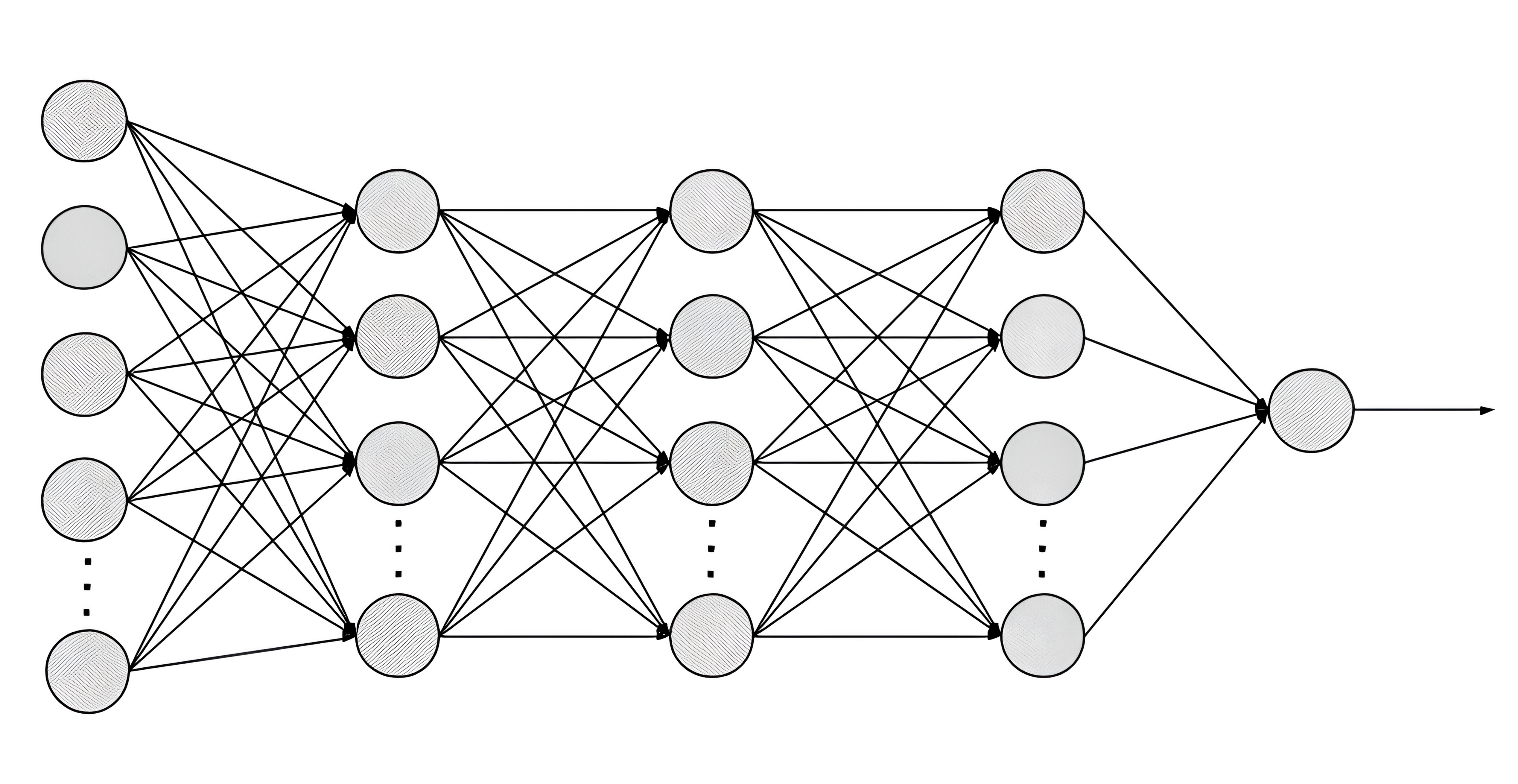
• Fully connected layers treat the positions of input features equally,
  so they do not structurally reflect order information between features:

  

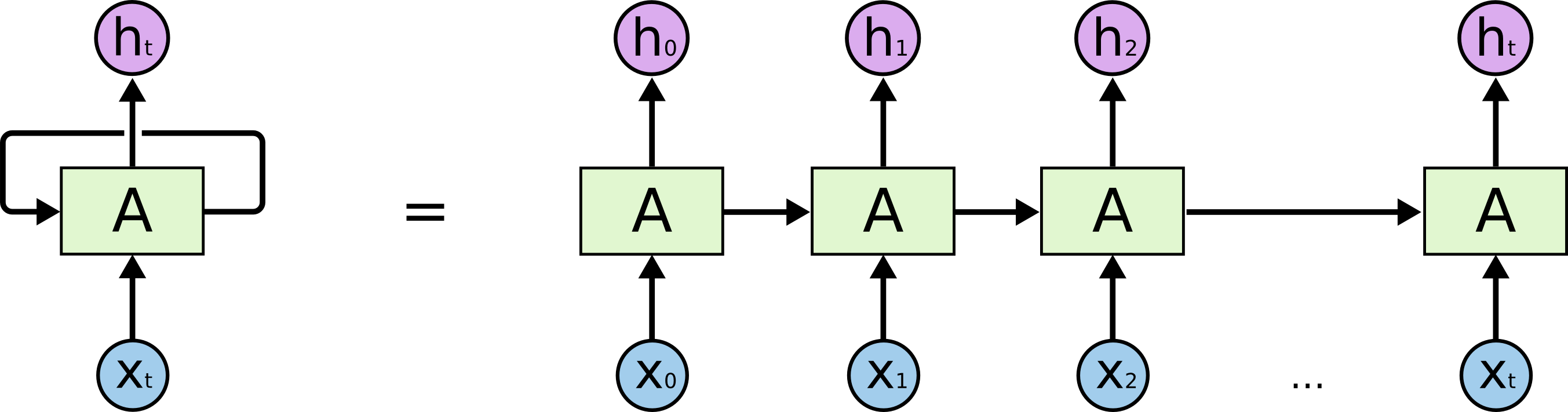
• RNN(Recurrent Neural Networks) involves preprocessing operations
  that preserve sequence information:

  

Vanilla RNN

---

• update hidden state $\overrightarrow{\mathbf{z}}_{t}$:

  \[\begin{aligned} \overrightarrow{\mathbf{z}}_{t} &= \text{tanh}(\mathbf{U}\cdot\overrightarrow{\mathbf{x}}_{t}+\mathbf{W}\cdot\overrightarrow{\mathbf{z}}_{t-1}+\overrightarrow{\mathbf{b}}_{h}) \end{aligned}\]
  • $\text{tanh}$ : activation function
  • $\overrightarrow{\mathbf{x}}_{t}$ : input value @ $t$
  • $\mathbf{U}$ : weight matrix of input value @ $t$
  • $\overrightarrow{\mathbf{z}}_{t-1}$ : hidden state @ $t-1$
  • $\mathbf{W}$ : weight matrix of hidden state @ $t-1$
  • $\overrightarrow{\mathbf{b}}_{h}$ : bias

• print output $\overrightarrow{\mathbf{y}}_{t}$

  \[\begin{aligned} \overrightarrow{\mathbf{y}}_{t} &= \text{softmax}(\mathbf{V}\cdot\overrightarrow{\mathbf{z}}_{t}+\overrightarrow{\mathbf{b}}_{o}) \end{aligned}\]
  • $\text{softmax}$ : activation function
  • $\overrightarrow{\mathbf{z}}_{t}$ : hidden state @ $t$
  • $\mathbf{V}$ : weight matrix of hidden state @ $t$
  • $\overrightarrow{\mathbf{b}}_{o}$ : bias

LSTM

---

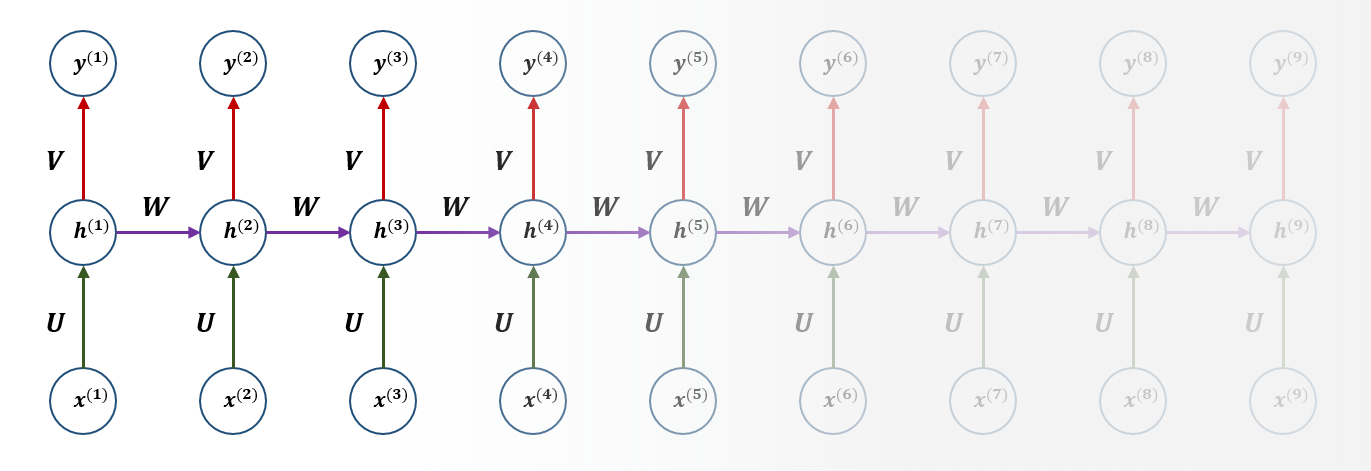
• vanilla rnn suffers from the problems of long-term dependencies:

  

  • Long-term dependencies are problems in which the initial order information is not preserved as the sequence gets longer due to the vanishing gradient.

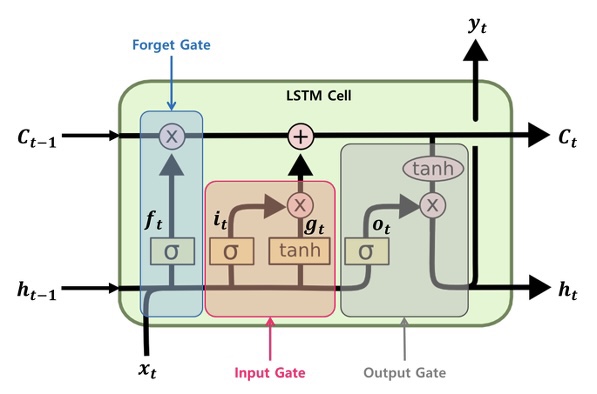
• LSTM(Long Short-Term Memory) is technique to alleviate vanishing gradient through gate adjustment:

  

  • forget gate: generate forget rule
  • input gate: generate remember rule and cell state update
  • cell state: determine how much to remember and how much to forget
  • output gate: generate hidden state and output

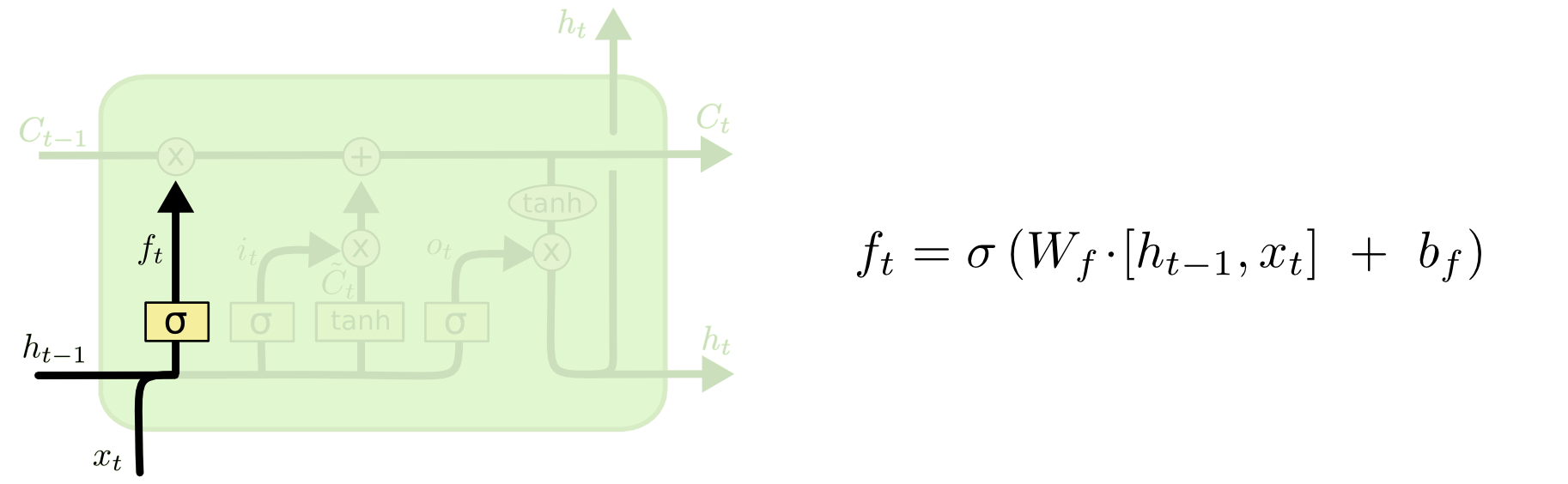
• forget gate:

  

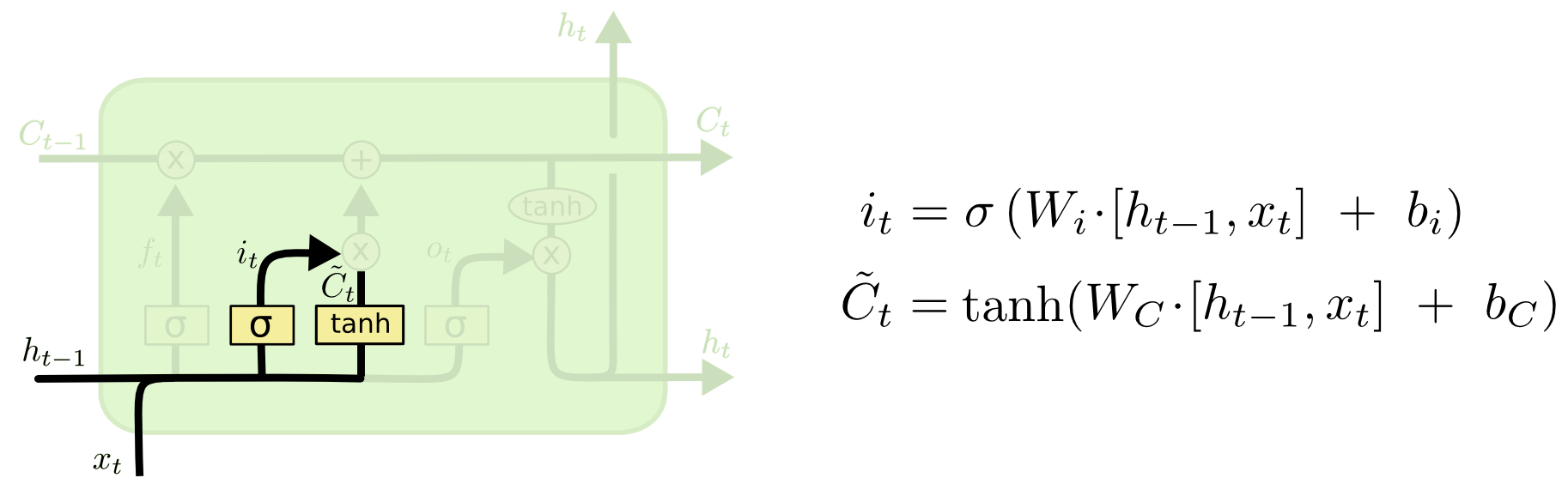
• input gate:

  

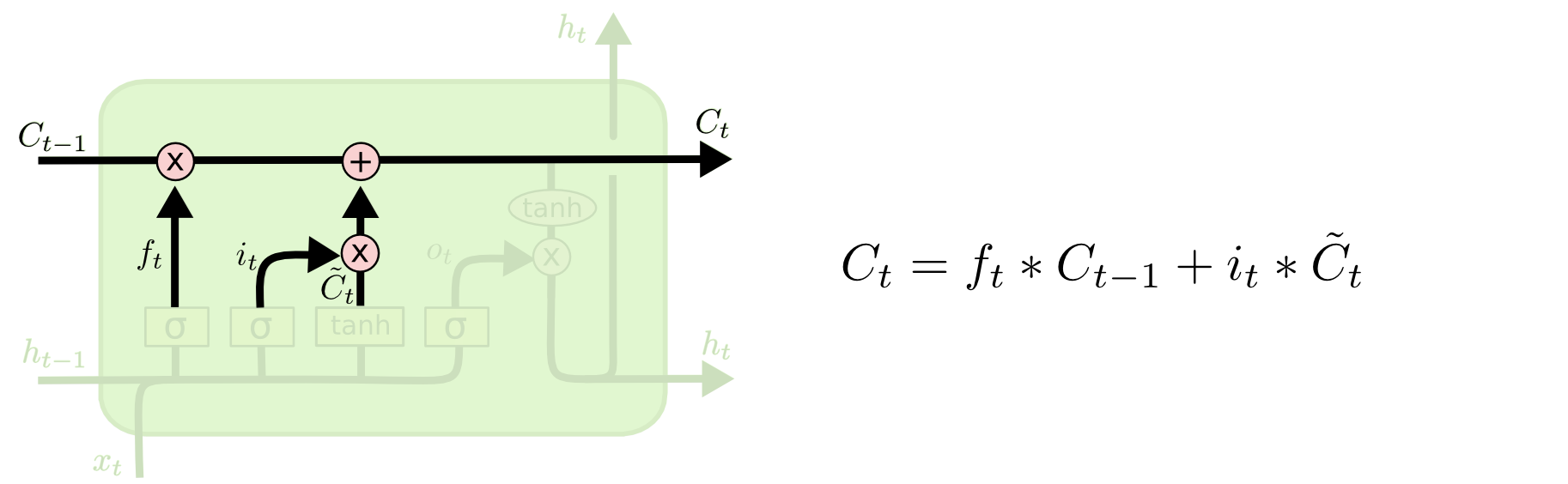
• cell state:

  

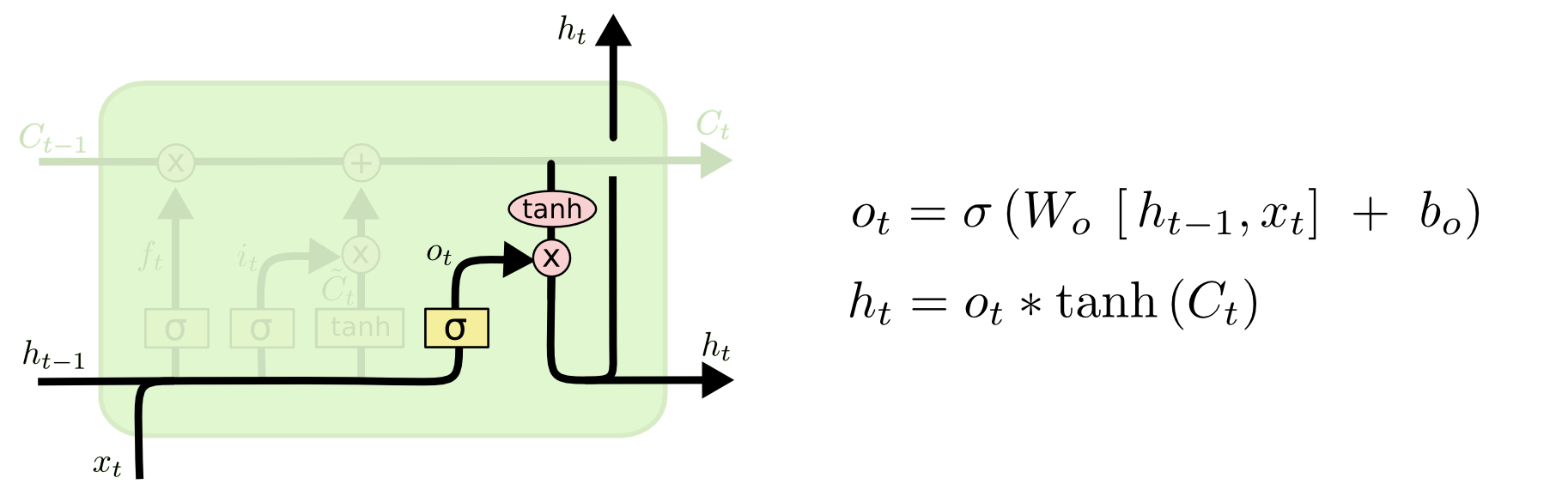
• output gate:

  

---

Sourse

• https://dgkim5360.tistory.com/entry/understanding-long-short-term-memory-lstm-kr