Simple Linear Regression Analysis

What? Linear Regression Analysis

---

• 선형 회귀 분석(Linear Regression Analysis) : 관찰된 연속형 변수들에 대하여 한 변수($Y$)를 다른 변수들($X$)의 선형 결합으로써 설명하는 모형을 탐색하는 방법
  • 광고지출비용이 증가할 때 매출액은 어떻게 변하는가?
  • 소득이 높은 국가의 국민들이 더 행복한가?
  • 소득이 증가할 때 소비는 얼마나 증가하는가?
  • 교육수준이 높을수록 임금이 증가하는가?
• 예측 대상이 되는 변수($Y$)
  • 반응변수(Response Variable)
  • 종속변수(Dependent Variable)
  • 내생변수(Endogenous Variable)
• 예측에 활용되는 변수($X$)
  • 설명변수(Explanatory Variable)
  • 독립변수(Independent Variable)
  • 외생변수(Exogenous Variable)

Simple Linear Regression Model

---

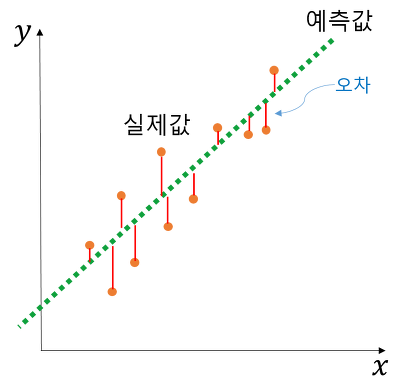
• 단순 선형 회귀 모형(Simple Linear Regression Model) : 반응변수와 단일 설명변수 간 선형 상관관계를 모델링하는 모형

  \[\begin{aligned} Y &=\beta_0+\beta_1X+\varepsilon\\ y_{i} &=\beta_0+\beta_1 x_{i}+\varepsilon_{i} \end{aligned}\]
• 회귀계수(Regression Coefficient) : 모형이 추론하고자 하는 모수(Parameter)로서 상수
  • 편향(Bias; $\beta_0$) : 설명변수의 값이 $0$ 일 때 종속변수의 값
  • 가중치(Weight; $\beta_1$) : 설명변수가 종속변수에 미치는 영향력의 방향과 강도

• 오차항(Error Term; $\varepsilon$) : 확률변수

  \[\begin{aligned} \varepsilon = y-\left(\beta_{0} + \beta_{1} x \right) \sim N(0, \sigma^2) \end{aligned}\]

  • 잔차(Residual; $\epsilon$) : 최적 회귀계수 하 오차항의 추정치

    \[\epsilon=y-\left(\hat{\beta}_{0} + \hat{\beta}_{1} x \right)\]

t-Test for Regression Coefficients

---

• t 검정(t-Test): 반응변수와 설명변수 간 상관관계의 통계적 유의성에 관한 가설 검정으로서, 두 변수 간 선형관계 혹은 인과관계의 유의성을 보장하지는 않음

• 모수(Parameter) 정의:

  \[\begin{aligned} \beta_{1} \end{aligned}\]

• 점 추정량(Point Estimator) 도출:

  \[\begin{aligned} \hat{\beta}_{1} \sim \mathcal{N}(\mathbb{E}\left[\hat{\beta}_{1}\right], \mathrm{SE}\left[\hat{\beta}_{1}\right]^2), \quad n > 30 \end{aligned}\]

  • 최소자승추정량의 평균:

    \[\mathbb{E}\left[\hat{\beta}_{1}\right] = \beta_{1}\]

  • 최소자승추정량의 분산:

    \[\mathrm{SE}\left[\hat{\beta}_{1}\right]^2 = \sigma^2\left[\displaystyle\frac{1}{\sum_{i=1}^{n}{(x_{i}-\overline{x})^2}}\right], \quad \varepsilon \sim \mathcal{N}(0,\sigma^2)\]
• 가설(Hypothesis) 설정:
  • $H_{0}: \quad \beta_{1} = 0$
  • $H_{1}: \quad \beta_{1} \ne 0$

• 검정통계량(Test Statistic):

  \[\begin{aligned} T = \frac{\hat{\beta}_{1}-0}{\mathrm{SE}\left[\hat{\beta}_{1}\right]} \sim t(n-2) \end{aligned}\]

Goodness of Fit

---

• 적합도(Goodness of Fit): 모형이 반응변수의 변동을 얼마나 잘 설명하고 있는가

• 반응변수(Response Variable):

  • 관측치 기반 회귀식:

    \[y_i = \beta_0 + \beta_1 x_i + \varepsilon_i, \quad \varepsilon_i \overset{\text{i.i.d}}{\sim} \mathcal{N}(0, \sigma^2)\]

  • 추정치 기반 회귀식:

    \[\hat{y}_i = \hat{\beta}_0 + \hat{\beta}_1 x_i\]

  • 회귀선은 평균을 지나감:

    \[\overline{y} = \hat{\beta}_0 + \hat{\beta}_1 \overline{x}\]

• 반응변수의 변동성(Variability):

  \[\begin{aligned} \sum_{i=1}^{n}{\left(y_{i}-\overline{y}\right)^2} &= \sum_{i=1}^{n}{\left[\left(\hat{y}_{i} + \varepsilon_{i}\right) -\overline{y}\right]^{2}} \\ &= \sum_{i=1}^{n}{\left[\left(\hat{y}_{i} -\overline{y}\right) + \varepsilon_i \right]^{2}} \\ &= \sum_{i=1}^{n}{\left[\left(\hat{y}_{i} -\overline{y}\right)^2 + \varepsilon_{i}^{2} + 2 \times \varepsilon_{i} \times \left(\hat{y}_{i}-\overline{y}\right)\right]} \\ &= \sum_{i=1}^{n}{\left(\hat{y}_{i} -\overline{y}\right)^{2}} + \sum_{i=1}^{n}{\varepsilon_{i}^2} + 2\times\sum_{i=1}^{n}{\varepsilon_{i}\left(\hat{y}_{i}-\overline{y}\right)} \\ &= \sum_{i=1}^{n}{\left(\hat{y}_{i} -\overline{y}\right)^2} + \sum_{i=1}^{n}{\varepsilon_{i}^{2}}\quad(\because \sum_{i=1}^{n}{\hat{y}_{i}-\overline{y}} = 0) \end{aligned}\]

• 총변동(Total Sum of Square) : 반응변수의 총 변동성

  \[\mathrm{TSS} =\sum_{i=1}^{n}{\left(y_{i}-\overline{y}\right)^2}\]

• 회귀변동(Explained Sum of Square) : 모형에 의해 설명되는 반응변수의 변동성

  \[\mathrm{ESS} =\sum_{i=1}^{n}{\left(\hat{y}_{i}-\overline{y}\right)^2}\]

• 잔차변동(Residual Sum of Square) : 모형에 의해 설명되지 않는 반응변수의 변동성

  \[\begin{aligned} \mathrm{RSS} &=\sum_{i=1}^{n}{\left(y_{i}-\hat{y}_{i}\right)^{2}}\\ &=\sum_{i=1}^{n}{\varepsilon_{i}^{2}} \end{aligned}\]

• 결정계수(Coefficient of Determination; $R^2$) : 총변동 대비 회귀변동의 비율로 측정된 적합도

  \[\begin{aligned} R^2 &= \frac{\mathrm{ESS}}{\mathrm{TSS}} \\ &= \frac{\mathrm{ESS}}{\mathrm{ESS} + \mathrm{RSS}} \\ &= 1 - \frac{\mathrm{RSS}}{\mathrm{TSS}} \end{aligned}\]