Statistical Inference

Estimation

---

Point Estimator

• 점 추정량(Point Estimator) : 모수를 추정하는 하나의 값(Single Value)

  	표기	평균	분산	비율
  모수	$\theta$	$\mu$	$\sigma^2$	$\pi$
  점 추정량	$\hat{\theta}$	$\overline{X}$	$S^2$	$P$

• 좋은 점 추정량의 성질

  • 불편성(Unbiasedness) : 기대값이 모수와 같아 모수로부터 음이나 양으로 편향되지 아니함
  • 효율성(Efficiency) : 모수의 불편 추정량 가운데에서 분산이 최소임
  • 일치성(Consistency) : 표본의 크기 $n$ 이 커질수록 평균자승오차가 $0$ 에 수렴함

불편 추정량(Unbiased Estimator)

• 정의 : 기대값이 모수와 같아 모수로부터 음이나 양으로 편향되지 아니한 추정량

  불편 추정량은 평균적으로 모수를 음으로 편향되게 평가하거나(과소평가), 양으로 편향되게 평가(과대평가)하지 않음. 단, 불편 추정량에 대하여 특정 표본에서 도출된 일부 실현값에는 오차가 존재할 수 있음.

  \[\begin{aligned} Bias(\hat{\theta}) &= E(\hat{\theta}) - \theta \\ &= 0 \end{aligned}\]
  • $Bias(\hat{\theta})$ : 모수 $\theta$ 의 추정량 $\hat{\theta}$ 에 대하여 그 편향(Bias)
  • $E(\hat{\theta})$ : 모수 $\theta$ 의 추정량 $\hat{\theta}$ 에 대하여 그 기대값

• 예시

  • 표본평균 $\overline{X}$ 은 모평균 $\mu$ 의 불편 추정량임
  • 표본분산 $S^2$ 은 모분산 $\sigma^2$ 의 불편 추정량임

효율적 추정량(Efficient Estimator)

• 정의 : 모수의 불편 추정량 가운데에서 분산이 최소인 불편 추정량

  \[\begin{aligned} \min{MSE(\theta, \hat{\theta})} &= \min{E\left[(\hat{\theta}-\theta)^2\right]}\\ &= \min{\bigg[Var(\hat{\theta}) + Bias(\hat{\theta})^2\bigg]} \end{aligned}\]
  • $MSE(\theta, \hat{\theta})$ : 모수 $\theta$ 의 추정량 $\hat{\theta}$ 에 대한 평균자승오차(Mean Squared Error)
  • $E[(\hat{\theta}-\theta)^2]$ : 모수 $\theta$ 의 추정량 $\hat{\theta}$ 에 대하여 그 오차 자승의 기대값

• 예시

  • 표본평균 $\overline{X}$ 은 모평균 $\mu$ 의 불편 선형 추정량(Unbiased Linear Estimator) 중 가장 효율적인 추정량(Best Linear Unbiased Estimator; BLUE) 임
    • 선형 추정량 : \(w_1x_1 + w_2x_2+\cdots+e\)
    • 비선형 추정량 : \(x_1^2,\quad x_1 \times x_2,\quad \displaystyle\frac{x_1}{x_2}\)

일치 추정량(Consistent Estimator)

• 정의 : 표본의 크기 $n$ 이 커질수록 평균자승오차가 $0$ 에 수렴하는 추정량

  \[\begin{aligned} \displaystyle\lim_{n \rightarrow \infty}{MSE(\hat{\theta})} &= \displaystyle\lim_{n \rightarrow \infty}{Var(\hat{\theta})} + \displaystyle\lim_{n \rightarrow \infty}{Bias(\hat{\theta})}^2\\ &= 0 \end{aligned}\]

• 예시

  • 표본평균 $\overline{X}$ 은 모평균 $\mu$ 의 일치 추정량임

Confidence Intervals

• 정의 : 신뢰 가능한 수준 하에서 모수를 포함할 수 있다고 추정되는 구간으로서 신뢰수준을 담보한 구간 추정량(Interval Estimator)

  표본평균 $\overline{X}$ 이 모평균 $\mu$ 의 좋은 점 추정량이라고 해서 항상 그 실현값 $\overline{x}_i$ 가 $\mu$ 와 일치하지는 않음. 때문에 특정 표본에서 구한 추정치 $\overline{x}_i$ 를 활용하여 $\mu$ 를 포함할 가능성이 있는 구간을 만들어서 $\mu$ 을 추정함. 신뢰구간은 이러한 구간 추정량에 대하여 $\mu$ 를 포함할 가능성을 담보하고 있음.

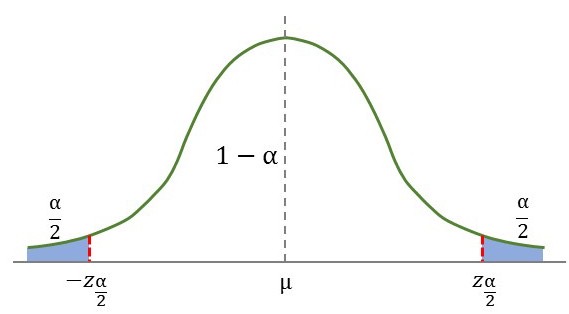
• 구성

  \[\text{CI}=\left(\overline{X}-z_{\alpha/2}\times \frac{\sigma}{\sqrt{n}}, \overline{X}+z_{\alpha/2}\times \frac{\sigma}{\sqrt{n}}\right)\]

  • 신뢰수준(Confidence Level; $1-\alpha$) : 신뢰구간이 담보하는, 해당 구간이 모수 $\mu$ 를 포함할 가능성

    \[P(\mu \in \text{CI})=1-\alpha\]

  • 오차한계(Margin of Error; \(z_{\alpha / 2}\times \displaystyle\frac{\sigma}{\sqrt{n}}\)) : 모수 $\mu$ 와 그 점 추정량 $\overline{X}$ 에 대하여 신뢰구간의 끝(한계)과 $\mu$ 사이의 최대 차이로서, $\mu$ 와 $\overline{X}$ 의 차이(오차)를 수용할 수 있는 범위를 결정하는 값

• 길이

  \[\text{Length}(\text{CI}) = 2 \times z_{\alpha/2} \times \frac{\sigma}{\sqrt{n}}\]
  • $(1-\alpha)\uparrow \; \Rightarrow L\uparrow$ : 신뢰수준이 높을수록 신뢰구간의 길이가 증가함
  • $\sigma\uparrow \; \Rightarrow L\uparrow$ : 모집단의 분포가 널리 퍼져 있을수록 정확한 추정이 어려워 신뢰구간의 길이가 증가함
  • $n\downarrow \; \Rightarrow L\uparrow$ : 표본의 크기가 작을수록 정확한 추정이 어려워 신뢰구간의 길이가 증가함

• 도출

  • 중심극한정리에 의해 $n$ 이 충분히 크면 다음이 성립함

    \[\begin{aligned} \overline{X} \sim N(\mu, \frac{\sigma^2}{n}) \end{aligned}\]

  • 확률변수 $\overline{X}$ 를 다음과 같이 표준화할 수 있음

    \[\begin{aligned} Z=\displaystyle\frac{\overline{X} - \mu}{\displaystyle\frac{\sigma}{\sqrt{n}}} \sim N(0,1) \end{aligned}\]

  • $100(1-\alpha)\%$ 신뢰수준 하 신뢰구간은 다음과 같음

    \[\begin{aligned} P(-z_{\alpha/2}<Z<z_{\alpha/2}) &=P(-z_{\alpha/2}<\displaystyle\frac{\overline{X}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}}<z_{\alpha/2})\\ &=P(-z_{\alpha/2}\times \displaystyle\frac{\sigma}{\sqrt{n}}<\overline{X}-\mu<z_{\alpha/2}\times \displaystyle\frac{\sigma}{\sqrt{n}})\\ &=P(-\overline{X}-z_{\alpha/2}\times \displaystyle\frac{\sigma}{\sqrt{n}}<-\mu<-\overline{X}+z_{\alpha/2}\times \displaystyle\frac{\sigma}{\sqrt{n}})\\ &=P(\overline{X}-z_{\alpha/2}\times \displaystyle\frac{\sigma}{\sqrt{n}}<\mu<\overline{X}+z_{\alpha/2}\times \displaystyle\frac{\sigma}{\sqrt{n}})\\ &=1-\alpha \end{aligned}\]

Hypothesis Testing

---

• 통계적 가설(Statistical Hypothesis) : 모집단의 모수에 대한 주장
  • 귀무가설(Null-Hypothesis; $H_0$) : 사실이 아니라는 충분한 근거를 얻기 전에는 사실이라고 믿어지는 가설
  • 대립가설(Alternative Hypothesis; $H_1$) : 연구자의 주장으로서 귀무가설이 기각될 때 채택되는 가설
• 가설검정(Hypothesis Testing) : 귀무가설을 기각할 충분한 증거가 있는지 살핌으로써 대립가설을 우회로 증명하는 절차
  1. 귀무가설과 대립가설 설정
  2. 유의수준 설정
  3. 모수 추정법 적용 가능 여부 검토
  4. 검정통계량과 p-value 도출
  5. 귀무가설 기각 여부 결정
  6. 검정 결과 해석

종류

• 양측검정(Two-Sided Test) : 귀무가설에 대한 기각역을 양측에 설정하는 검정

  

  \[\begin{aligned} H_0&:\;\mu=70,\\ H_1&:\;\mu\ne70 \end{aligned}\]

• 단측검정(One-Sided Test) : 귀무가설에 대한 기각역을 단측에만 설정하는 검정

  • 우측검정 : 기각역을 우측에만 설정하는 검정

    

    \[\begin{aligned} H_0&:\;\mu \le 70,\\ H_1&:\;\mu > 70 \end{aligned}\]

  • 좌측검정 : 기각역을 좌측에만 설정하는 검정

    

    \[\begin{aligned} H_0&:\;\mu=70,\\ H_1&:\;\mu<70 \end{aligned}\]

오류와 신뢰성

• 오류(Error) : 사실과 다르게 판단함

  

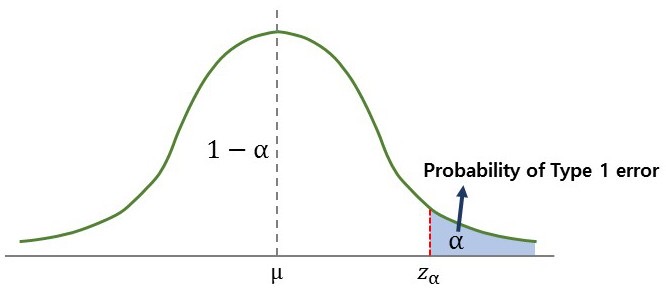
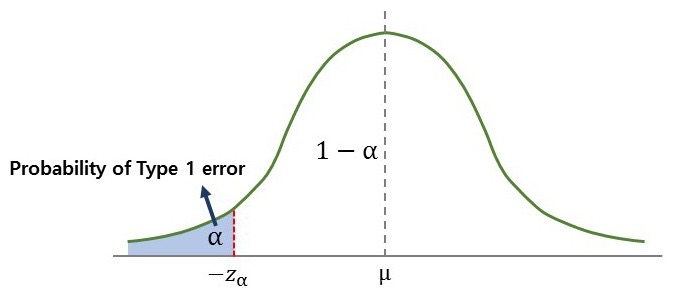
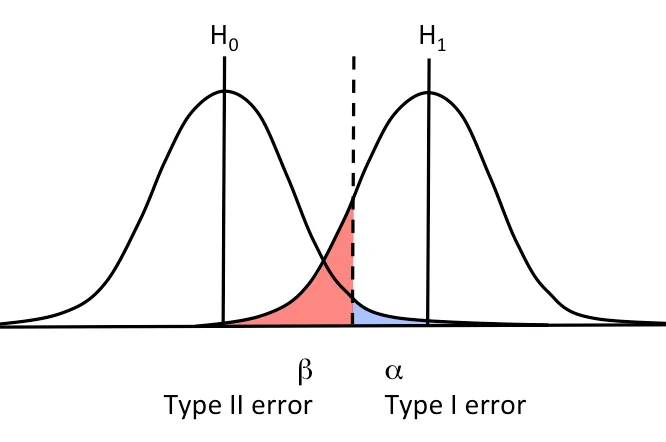
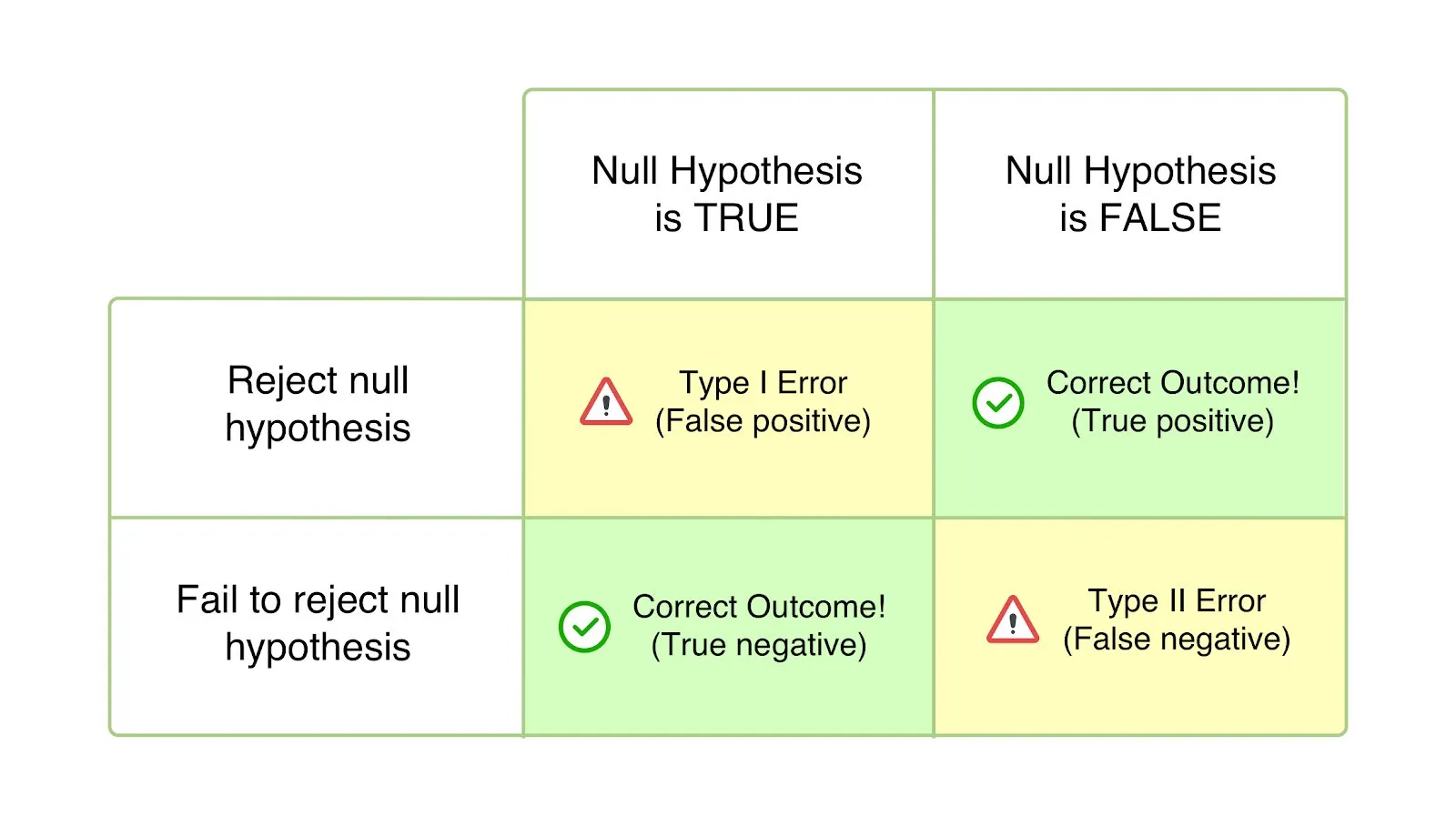
  • 제1종 오류(Type 1 Error) : 귀무가설이 참일 때 귀무가설을 기각하는 오류
  • 제1종 오류(Type 2 Error) : 귀무가설이 거짓일 때 귀무가설을 기각하지 않는 오류

• 검정의 유의수준(Significance Level) : 제1종 오류를 범할 확률

  \[\alpha\]
  • 통계학에서는 보수적 태도(귀무가설을 기각하지 않으려는 태도)를 취하므로 제1종 오류에 민감함

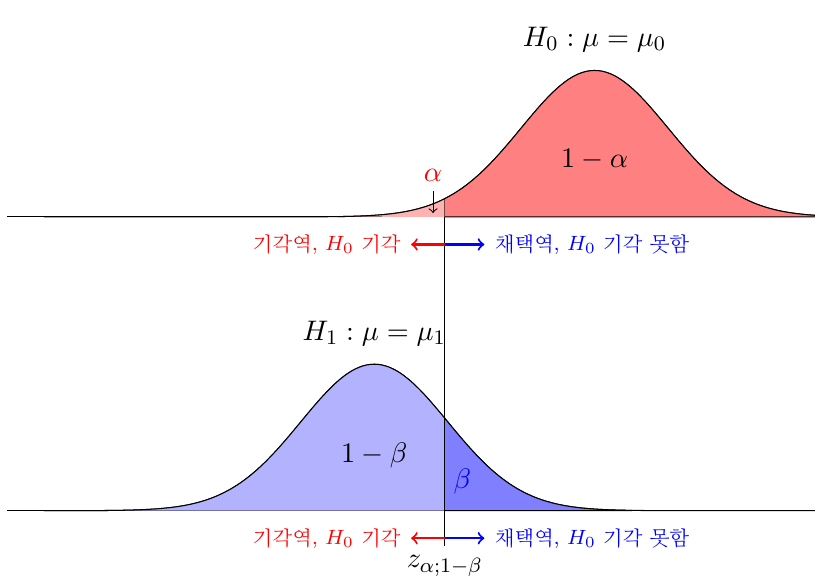
• 검정의 신뢰수준(Confidence Level) : 제1종 오류를 범할 확률 $\alpha$ 에 대하여, 귀무가설이 참일 때 귀무가설을 기각하지 않을 확률

  \[1-\alpha\]

• 검정의 검정력(Power) : 제2종 오류를 범할 확률 $\beta$ 에 대하여, 귀무가설이 거짓일 때 귀무가설을 기각할 확률

  \[1-\beta\]

검정통계량과 유의확률 도출

• 검정통계량(Test Statistic) : 귀무가설이 참이라고 가정했을 때 얻은 결과

  

  \[\begin{aligned} Z &=\displaystyle\frac{\overline{X}-\mu_0}{\displaystyle\frac{\sigma}{\sqrt{n}}} \\ &=\displaystyle\frac{\overline{X}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}} + \displaystyle\frac{\mu-\mu_0}{\displaystyle\frac{\sigma}{\sqrt{n}}} \\ &=0 + \displaystyle\frac{\mu-\mu_0}{\displaystyle\frac{\sigma}{\sqrt{n}}} \end{aligned}\]

  • 귀무가설이 참인 경우 검정통계량의 분포 : 평균이 $0$ 이고 분산이 $1$ 인 가우시안 분포를 따름

    \[\begin{aligned} Z \sim N(0,1) \end{aligned}\]

  • 귀무가설이 참이 아닌 경우 검정통계량의 분포 : 평균이 $\displaystyle\frac{\mu-\mu_0}{\displaystyle\frac{\sigma}{\sqrt{n}}}$ 이고 분산이 $1$ 인 가우시안 분포를 따름

    \[\begin{aligned} Z \sim N(\displaystyle\frac{\mu-\mu_0}{\displaystyle\frac{\sigma}{\sqrt{n}}},1) \end{aligned}\]

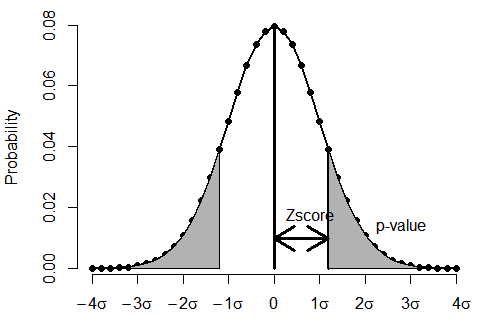
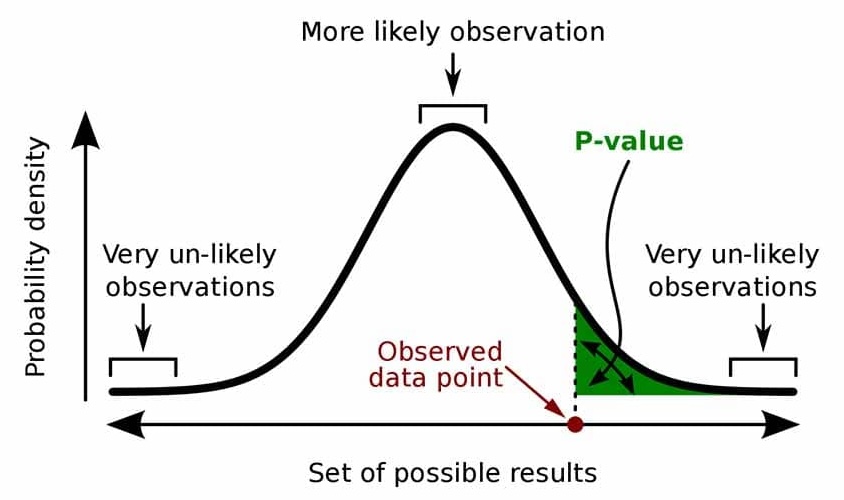
• 유의확률(Significance Probability Value; $\text{p-value}$) : 검정통계량($Z$)보다 극단적인 결과($Y$)가 관측될 확률로서, 표본이 귀무가설과 양립하는 정도

  

  \[\begin{aligned} \text{p-value} &= P\left(\vert Y \vert \ge \vert Z \vert \Big\vert H_{0}\right) \quad \text{for}\; Y \sim N(0,1) \end{aligned}\]

귀무가설 기각 여부 결정

• 검정통계량 $Z$ 의 실현값 $z$ 가 $0$ 과 차이가 많이 나면 기각함

  \[\vert z \vert >z_{\alpha/2}\]
  • 기각치(Reject Value; $z_{\alpha/2}$) : 차이가 많이 나는 기준이 되는 값으로서, 유의수준 $\alpha$ 에 따라 결정됨

• 귀무가설이 참일 때 표본이 발생할 확률 $\text{p-value}$ 이 현저하게 낮으면 기각함

  \[\text{p-value} < \alpha\]
  • 유의수준(Significance Level; $\alpha$) : 현저하게 낮은 기준이 되는 값으로서, 제1종 오류 수용 정도

검정 결과 해석

• 통계적 유의성(Statistically Significant) : 유의함이 실제로는 존재하지 않을 수도 있지만, 주어진 정보를 활용하여 판단했을 때는 존재하였음

• 귀무가설을 기각할 수 없을 때는 귀무가설이 제한적으로 사실이라고 받아들임

  귀무가설을 $\alpha \times 100 \%$ 유의수준에서 기각하지 않는다. 즉, $\alpha \times 100 \%$ 유의수준에서 모평균 $\mu$ 는 $\mu_{0}$ 과 통계적으로 유의한 차이가 있다고 볼 수 없다.

• 귀무가설을 기각할 때는 대립가설이 사실이라고 잠정적으로 결론을 내림

  귀무가설을 $\alpha \times 100 \%$ 유의수준에서 기각한다. 즉, $\alpha \times 100 \%$ 유의수준에서 모평균 $\mu$ 는 $\mu_0$ 과 통계적으로 유의한 차이가 있다.

Student t-Dist.

---

모분산 $\sigma^2$ 을 모르는 경우 표본평균 $\overline{X}$ 에 대하여 가설검정 시 우선 표본분산 $S^2$ 을 활용하여 모분산 $\sigma^2$ 을 추정해야 함. 추정된 모분산으로 도출된 검정통계량은 자유도 $\nu$ 에 따라 그 폭이 상이한 분포를 따르게 됨. 이처럼 자유도에 따라 변화하는 분산의 변동성을 반영하기 위해 표준정규분포 $Z \sim N(0,1)$ 대신 스튜던트 t 분포 $T \sim t(\nu)$ 를 사용함.

• 스튜던트 t 분포($t(\nu)$) : 표준정규분포를 따르는 확률변수 $Z$ 와 자유도가 $\nu$ 인 카이제곱분포를 따르는 확률변수 $V$ 로 구성되는 확률변수의 분포

  

  \[T=\frac{Z}{\sqrt{\displaystyle\frac{V}{\nu}}} \quad \text{for}\;Z \sim N(0,1),\; V \sim \chi^2(\nu)\]

  • 카이제곱분포($\chi^2(\nu)$) : 자유도가 $\nu$ 로 주어졌을 때 표준정규분포를 따르는 독립적인 확률변수 $Z_{i}\left(=\displaystyle\frac{X_{i}-\overline{X}}{\sigma}\right)$ 들의 자승의 합의 분포로서, 모분산을 추정하는 데 사용됨

    \[\begin{aligned} V &=\sum_{i=1}^{k}{Z_{i}^2} \quad \text{for}\; Z_{\forall} \sim N(0,1)\\ &=\sum_{i=1}^{k}{\left(\frac{X_{i}-\overline{X}}{\sigma}\right)^2}\\ &=\frac{1}{\sigma^2} \times \sum_{i=1}^{k}{\left(X_{i}-\overline{X}\right)^2}\\ &=\frac{1}{\sigma^2} \times \nu \cdot \frac{1}{\nu} \sum_{i=1}^{k}{\left(X_{i}-\overline{X}\right)^2}\\ &=\nu \times \frac{S^2}{\sigma^2} \sim \chi^2(\nu) \end{aligned}\]

• 스튜던트 t 분포를 활용한 표본 $X \sim N(\mu, \sigma^2)$ 의 검정통계량 $T$ 도출

  \[\begin{aligned} T &= Z \times \frac{1}{\sqrt{\displaystyle\frac{V}{\nu}}}\\ &= \frac{\overline{X}-\mu}{\displaystyle\frac{\sigma}{\sqrt{n}}} \times \frac{1}{\sqrt{\displaystyle\frac{\sigma^2}{S^2}}}\\ &= \frac{\overline{X}-\mu}{\displaystyle\frac{S}{\sqrt{n}}} \sim t(\nu) \end{aligned}\]

---

이미지 출처

• https://u5man.medium.com/to-err-is-human-what-the-heck-is-type-i-and-type-ii-error-b2c78190a45c
• https://wikidocs.net/163986