What? Statistics
Based on the following lectures
(1) “Statistics (2018-1)” by Prof. Sang Ah Lee, Dept. of Economics, College of Economics & Commerce, Kookmin Univ.
(2) "Statistical Models and Application (2024-1)" by Prof. Yeo Jin Chung, Dept. of Data Science, The Grad. School, Kookmin Univ.
What? Statistics
-
통계학(Statistics)
의사결정에 필요한 정보를 얻기 위하여 데이터를 수집(Collect), 정리(Summarize), 분석(Analyze), 해석(Interpret)하는 방법을 연구하는 학문
-
종류
- 기술통계학(Descriptive Statistics) : 데이터를 수집, 정리, 제시, 요약하는 방법을 연구함
- 추론통계학(Inferential Statistics) : 표본으로부터 모집단의 성격을 추정하는 방법을 연구함
What? Descriptive Statistic
Data Set
- 구성
- 관측치(Observation) : 분석하려는 집합에 속한 하나의 개체
- 변수(Variable) : 개체의 특징
- Data Type
- 정량적 자료(Quantitative Data) : 수로 표현되는 자료로서 숫자 자체가 의미를 가지는 자료
- 이산형 자료(Discrete Data) : 셀 수 있는 정수 형태의 자료
- 연속형 자료(Continuous Data) : 셀 수 없는 실수 형태의 자료
- 정성적 자료(Qualitative Data) : 범주(Category)에 따라 나뉘는 자료
- 정량적 자료(Quantitative Data) : 수로 표현되는 자료로서 숫자 자체가 의미를 가지는 자료
Descriptive Statistic
-
기술통계량(Descriptive Statistic) : 숫자로 측정한 데이터 세트의 특징
- 명목 척도(Nominal Scale)
-
고유한 값(Unique Value)만을 구분하는 척도
전공 : 경영학, 경제학, 통계학
-
- 순서 척도(Ordinal Scale)
-
값들 사이에 분명한 순위가 있는 척도
직급 : 사원, 대리, 팀장, 과장, 차장, 부장
-
값의 간격은 의미를 갖지 않음
-
- 구간 척도(Interval Scale)
-
값의 간격이 산술적 의미를 갖는 척도
기온 $0^{\circ}C$ 와 $10^{\circ}C$ 의 간격은 기온 $20^{\circ}C$ 와 $30^{\circ}C$ 의 간격과 동일함
-
값 사이의 비율은 산술적 의미를 갖지 않음
기온 $30^{\circ}C$ 가 $20^{\circ}C$ 보다 $50%$ 더 따뜻하다고 볼 수 없음
-
- 비율 척도(Ratio Scale)
-
값 사이의 비율이 산술적 의미를 갖는 척도
순익 $2,000,000$ 원은 순익 $1,000,000$ 원 보다 순익 두 배라고 볼 수 있음
-
$0$ 이 절대영점으로서 의미를 가짐
매출 $0$ 원은 매출이 하나도 없음을 의미함
-
Summary Quantitative Data
-
중심 위치 측도 : 대표값으로서 값의 대부분이 어디쯤 위치하는지 측정하는 지표
-
변이 측도 : 관측치들이 얼마나 퍼져 있는가를 나타내는 측도
중심 위치 측도
-
평균(Mean; $\mu$) : 관측치들의 합을 그 갯수로 나눈 값
\[\mu = \frac{1}{N}\sum_{i=1}^{N}X_{i}\] -
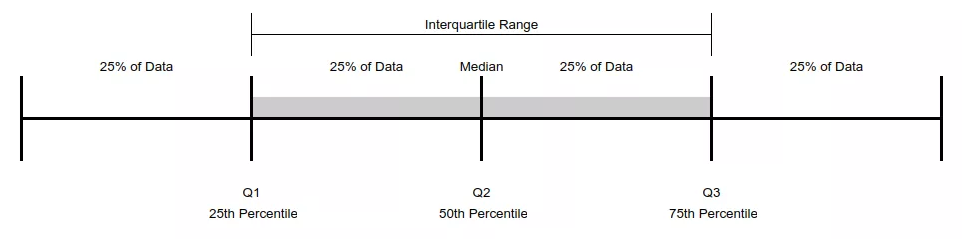
중위수(Median; $Q_2$) : 모든 관측치를 크기에 따라 오름차순 정렬했을 때 중앙에 오는 값
-
사분위수(Quartile; $Q_i$) : 모든 관측치를 크기에 따라 오름차순으로 정렬했을 때, 하위 25%($Q_1$), 하위 50%($Q_2$), 하위 75%($Q_3$)에 해당하는 값
변이 측도
-
범위(Range) : 최대값과 최소값의 차이
\[\text{R}=X_{max}-X_{min}\] -
사분위범위(Interquartile Range) : 관측치를 크기를 기준으로 오름차순 정렬했을 때 제3사분위수와 제1사분위수의 차이
\[\text{IQR}=Q_{3}-Q_{1}\] -
평균절대편차(Mean Absolute Deviation; MAD) : 관측치와 평균 사이 거리의 평균
\[\text{MAD} = \frac{1}{N}\sum_{i=1}^{N} \vert X_{i}-\mu \vert\] -
분산(Variance; $\sigma^2$) : 관측치와 평균 간 편차 자승의 평균
\[\sigma^2 = \frac{1}{N}\sum_{i=1}^{N}(X_{i}-\mu)^2\] -
표준편차(Standard Deviation; $\sigma$) : 분산의 자승근
\[\sigma = \sqrt{\frac{1}{N}\sum_{i=1}^{N}(X_{i}-\mu)^2}\]- 자료에서 사용된 단위와 동일한 단위로 측정되므로 해석에 용이함
변이 측도를 활용한 이상치 판별
-
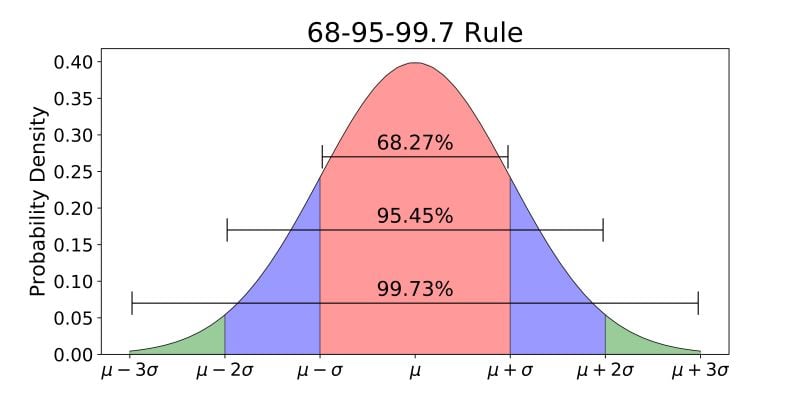
경험 법칙(Empirical Rule) : 관측치 분포가 종 모양의 대칭 형태를 띠는 경우, 실증적으로 획득된 분포에 대한 일반적인 원칙이 성립함
- $(\mu - 1\sigma, \mu + 1\sigma)$ 에는 관측치의 약 68%가 존재함
- $(\mu - 2\sigma, \mu + 2\sigma)$ 에는 관측치의 약 95%가 존재함
- $(\mu - 3\sigma, \mu + 3\sigma)$ 에는 관측치의 약 99%가 존재함
-
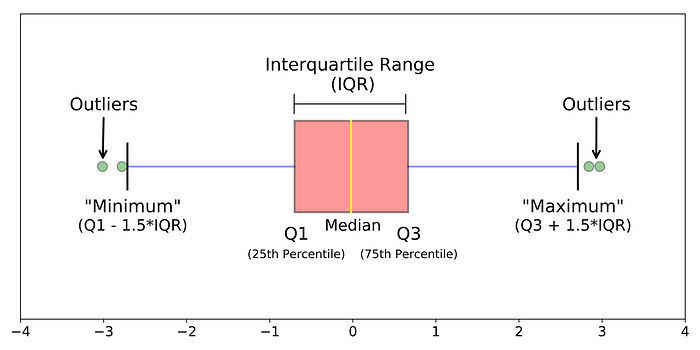
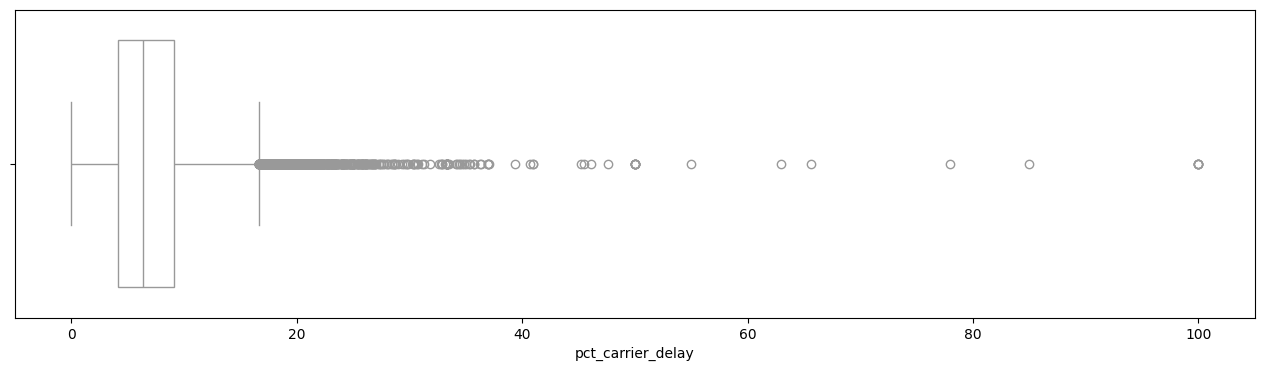
사분위수 범위를 활용한 이상치 판별
- 이상치 판단 기준으로서 상한선 및 하한선 설정
- 상한선 : $Q_{3}+1.5\cdot\text{IQR}$
- 하한선 : $Q_{1}-1.5\cdot\text{IQR}$
-
내부 범위 설정
\[\text{Outlier} \notin [Q_{1}-1.5\cdot\text{IQR}, Q_{3}+1.5\cdot\text{IQR}]\]
- 이상치 판단 기준으로서 상한선 및 하한선 설정
변수 간 관계
-
공분산(Covariance) : 두 변수의 편차(관측치와 평균 사이 거리)를 곱한 값의 평균
\[\sigma_{XY} = \frac{1}{N}\sum_{i=1}^{N}(X_{i}-\mu_X)(Y_{i}-\mu_Y)\]- $\sigma_{XY} > 0$ : 변수 $X, Y$ 가 양의 상관관계를 가짐
- $\sigma_{XY} < 0$ : 변수 $X, Y$ 가 음의 상관관계를 가짐
- $\sigma_{XY} = 0$ : 변수 $X, Y$ 간에 상관관계가 유의미하다고 볼 수 없음
-
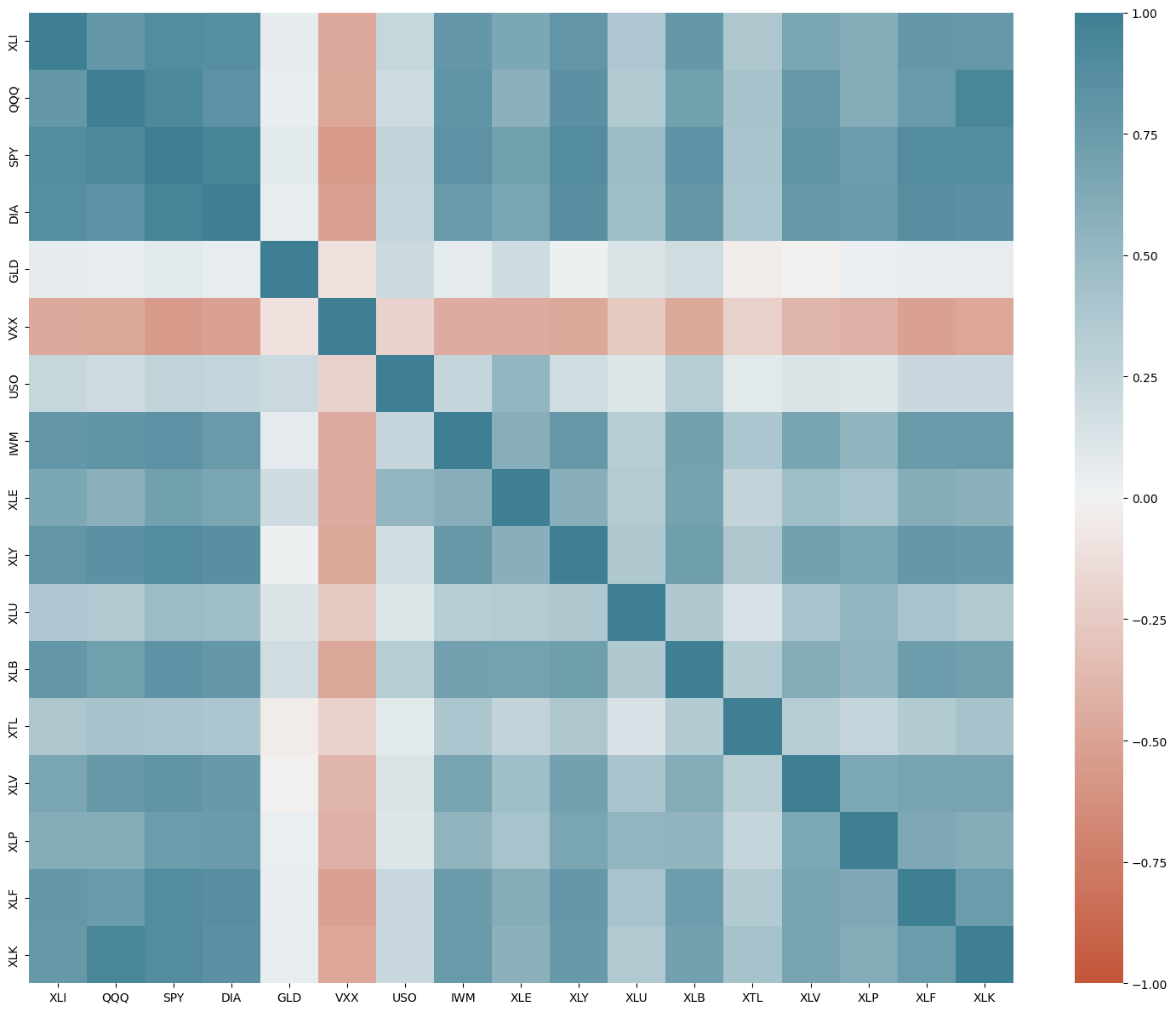
피어슨 상관계수(Pearson Correlation Coefficient; PCC) : 공분산의 단위 의존적(Unit-Dependent)인 문제를 완화한 지표로서, 공분산을 두 변수의 편차의 곱으로 나눈 값
\[\rho_{XY} = \frac{\sigma_{XY}}{\sigma_{X}\sigma_{Y}}\]- $-1\le\rho_{XY}\le1$
- $\rho_{XY} > 0$ : 변수 $X, Y$ 가 양의 상관관계를 가짐
- $\rho_{XY} < 0$ : 변수 $X, Y$ 가 음의 상관관계를 가짐
- $\rho_{XY} = 0$ : 변수 $X, Y$ 간에 상관관계가 유의미하다고 볼 수 없음
Summary with Graphs
수치형 변수
-
Box Plot : 사분위수를 기준으로 데이터의 대략적인 분포를 나타낸 그래프
-
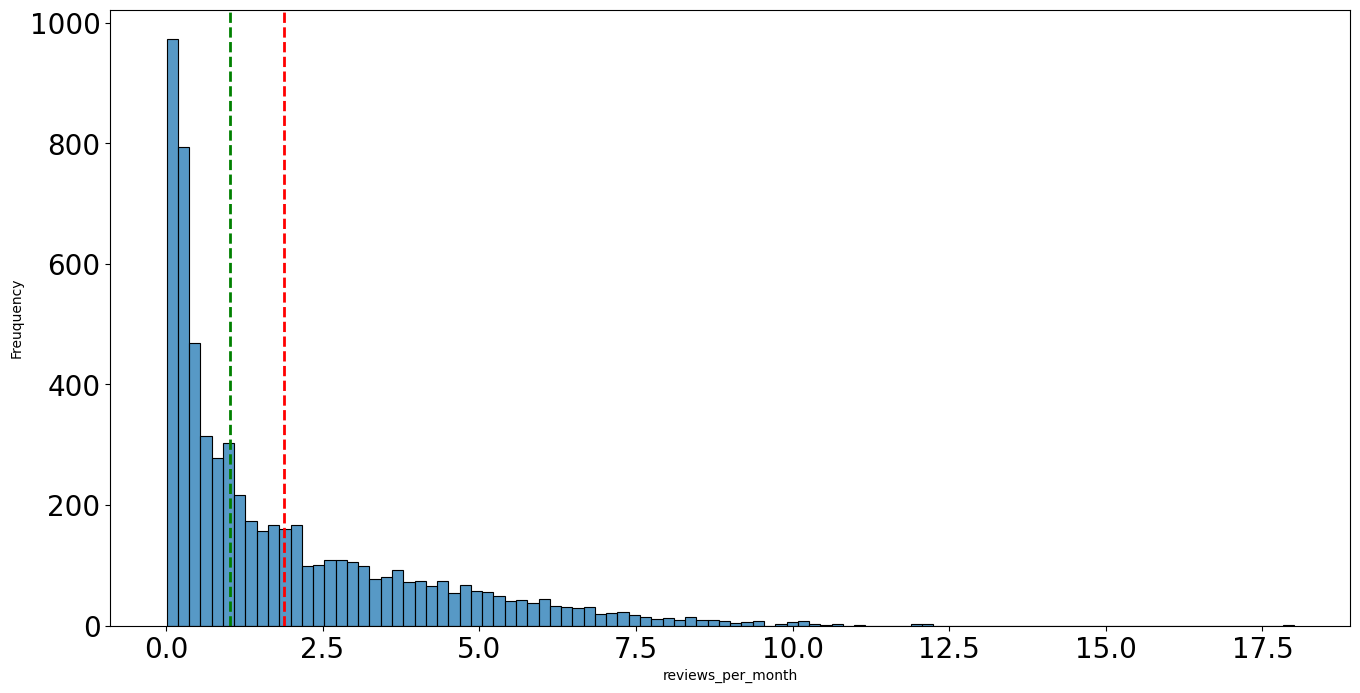
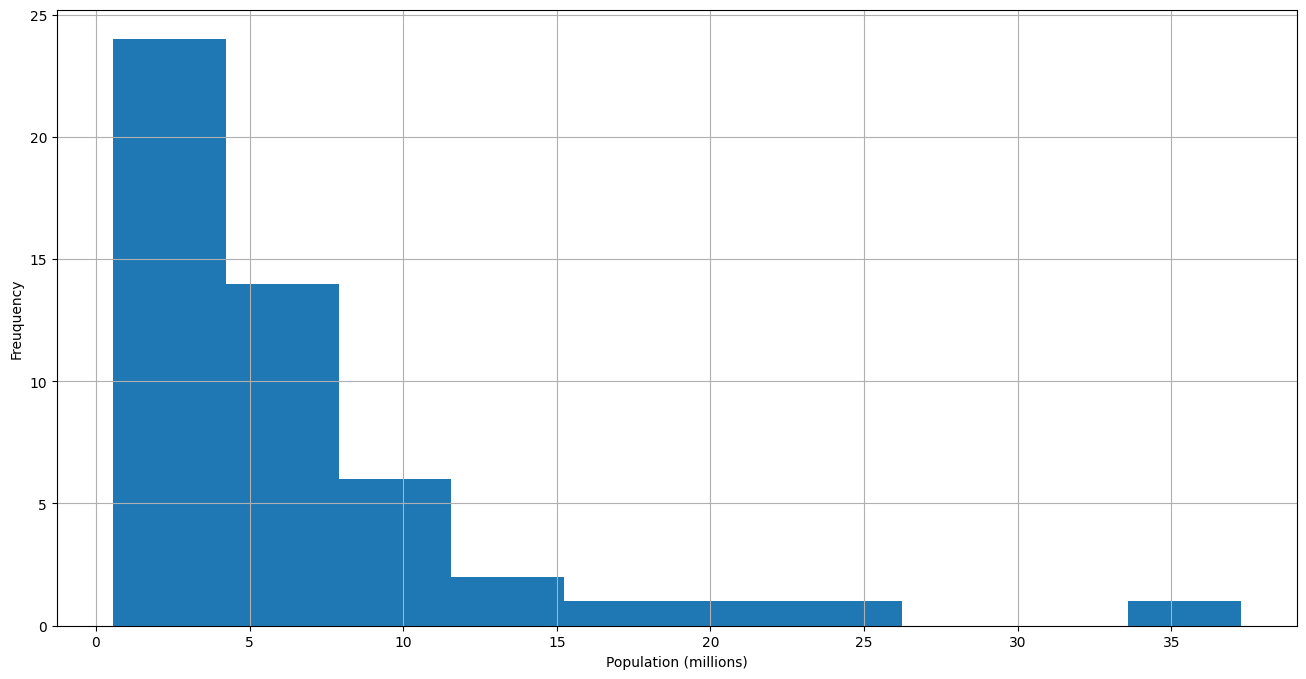
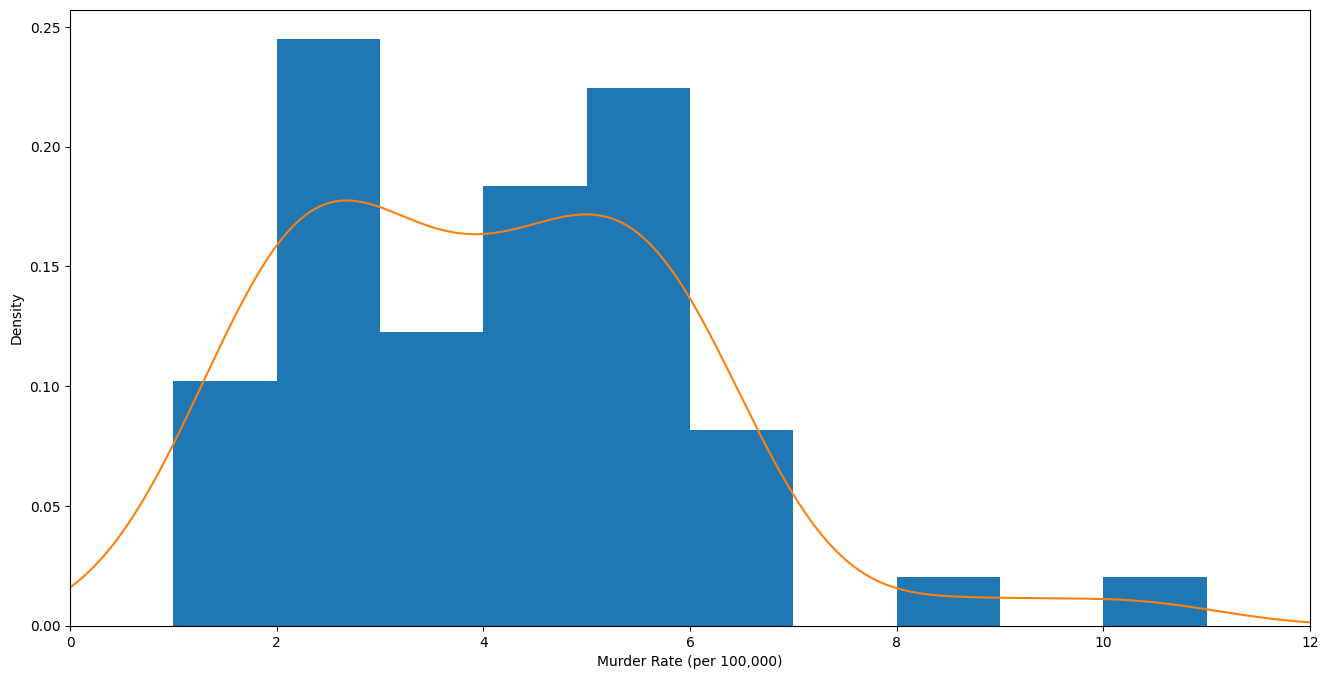
Histogram : 데이터 범위를 동일 간격 구간으로 나누어 해당 구간에 위치한 데이터 갯수를 나타낸 그래프
-
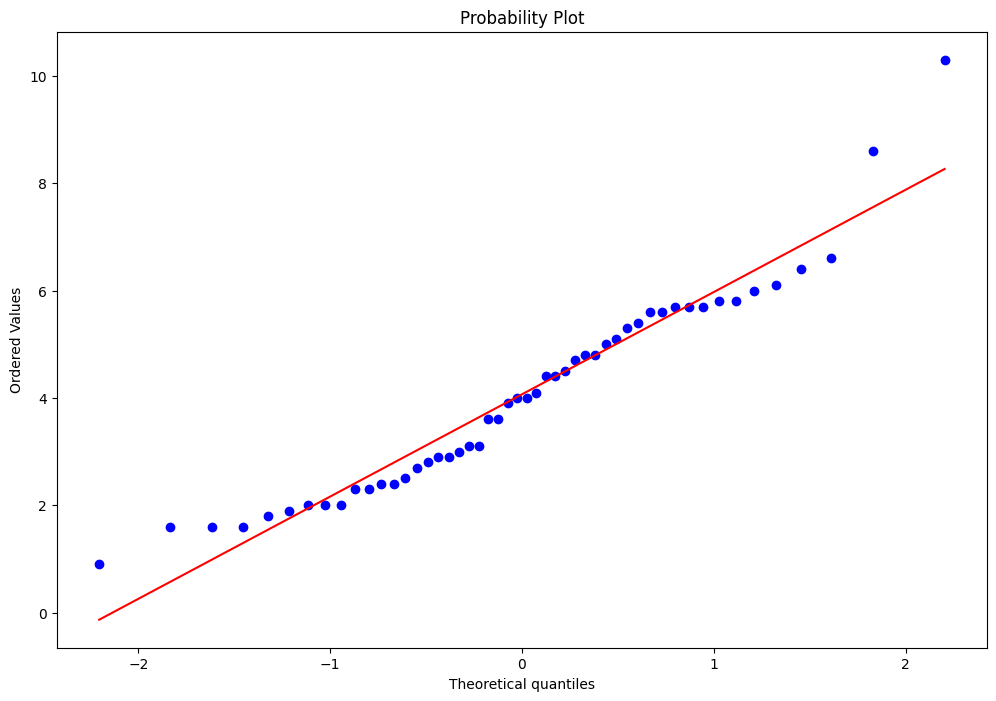
Q-Q Normality Plot : 데이터 분포 형태가 정규 분포에 얼마나 근접한지 나타내는 그래프
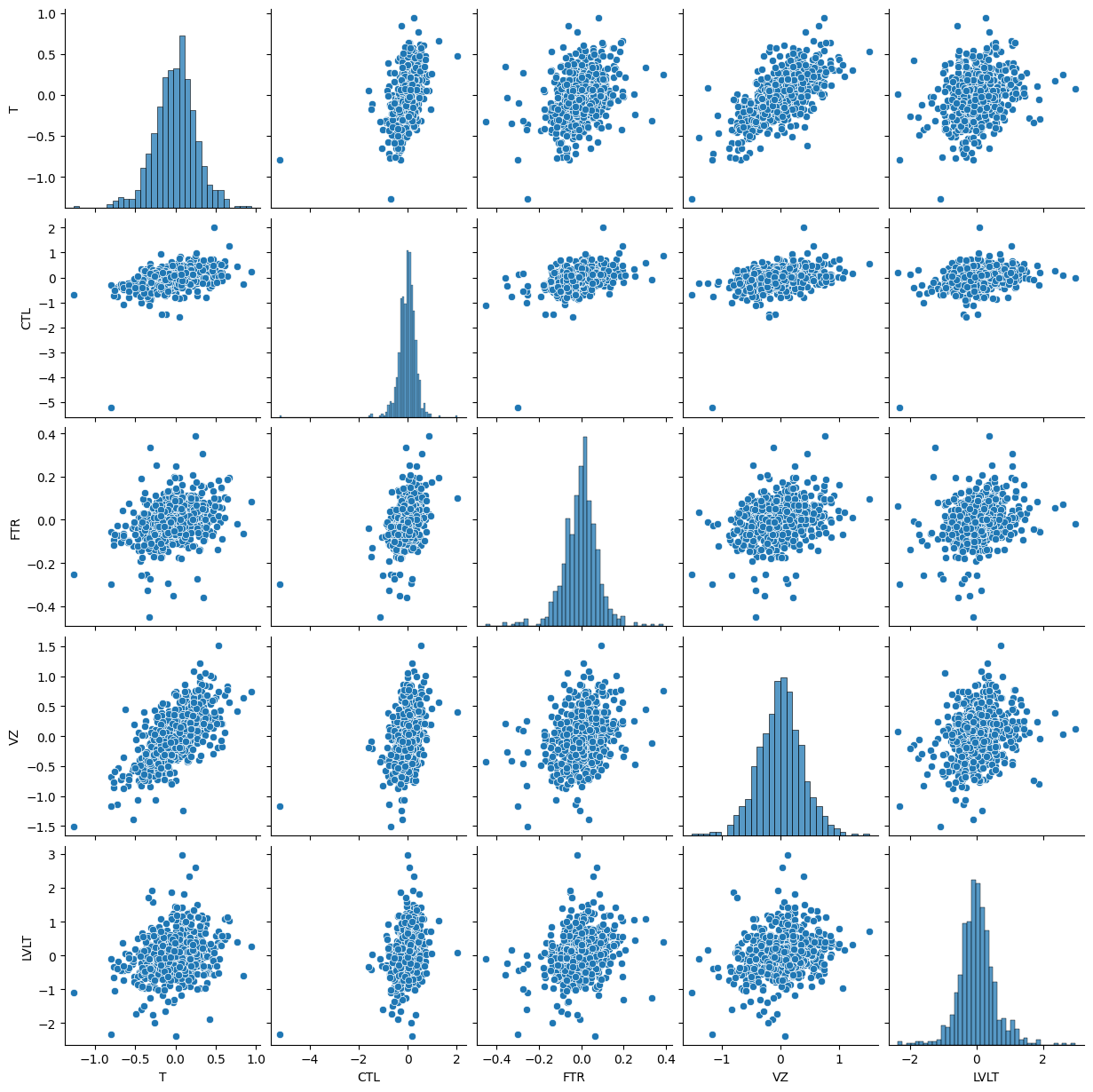
수치형 변수 간 관계
범주형 변수
-
도수분포표(Frequency Table) : 각 범주에 해당하는 관측치 갯수를 요약한 표
-
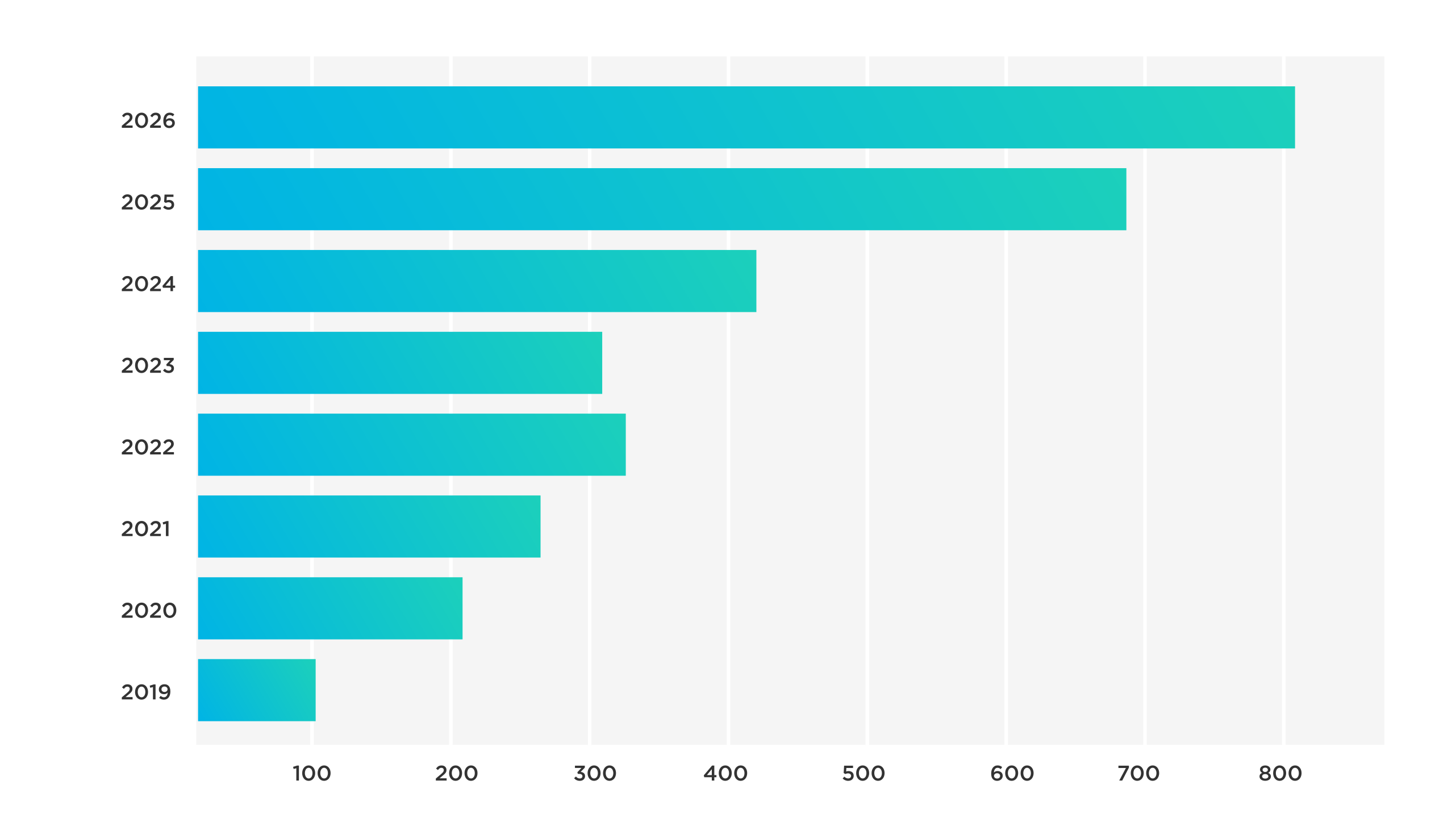
Bar Plot : 도수분포표의 값을 막대 높이로 나타낸 그래프
-
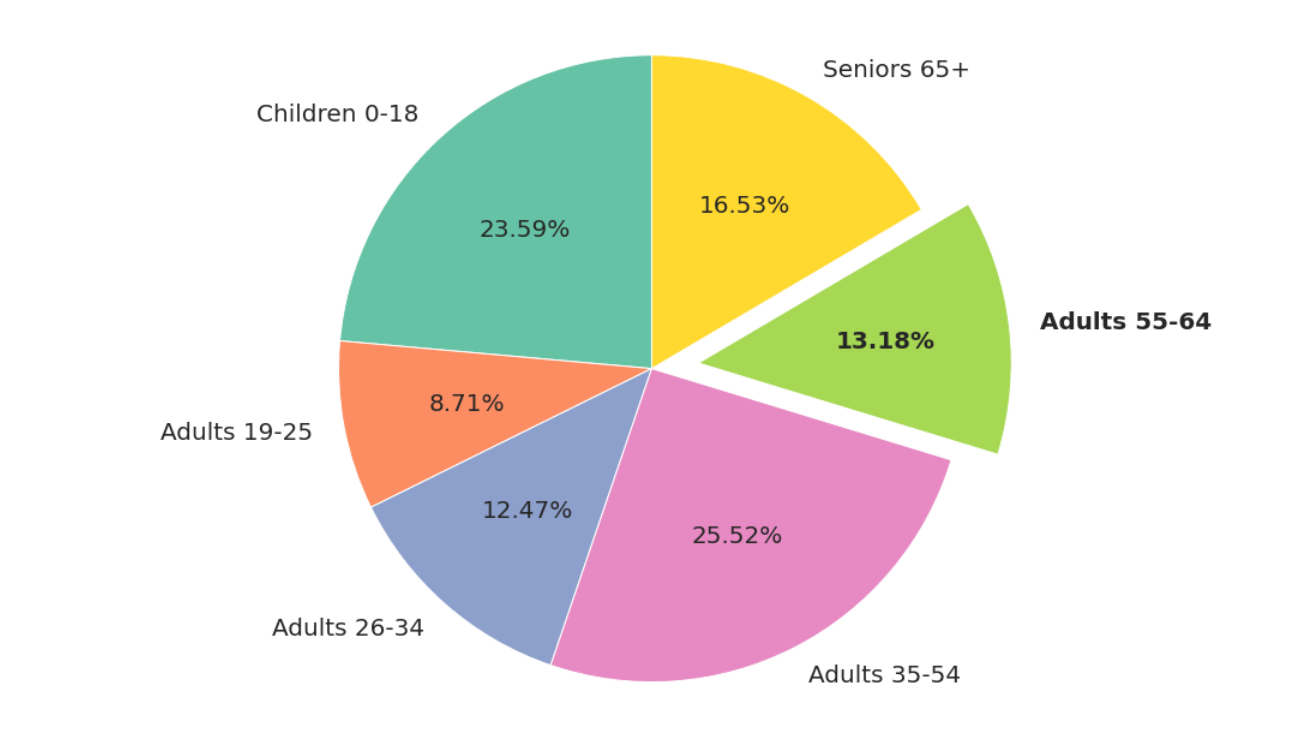
Pie Chart : 도수분포표의 빈도 비율을 부채꼴 모양으로 나타낸 그래프
범주형 변수 간 관계
-
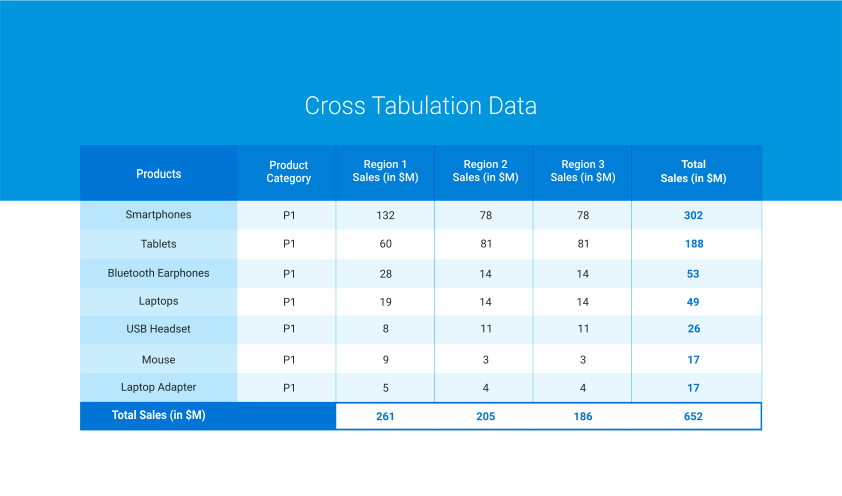
분할표(Cross Table) : 두 범주형 변수에 의해 생성되는 범주별 빈도수를 요약한 표
-
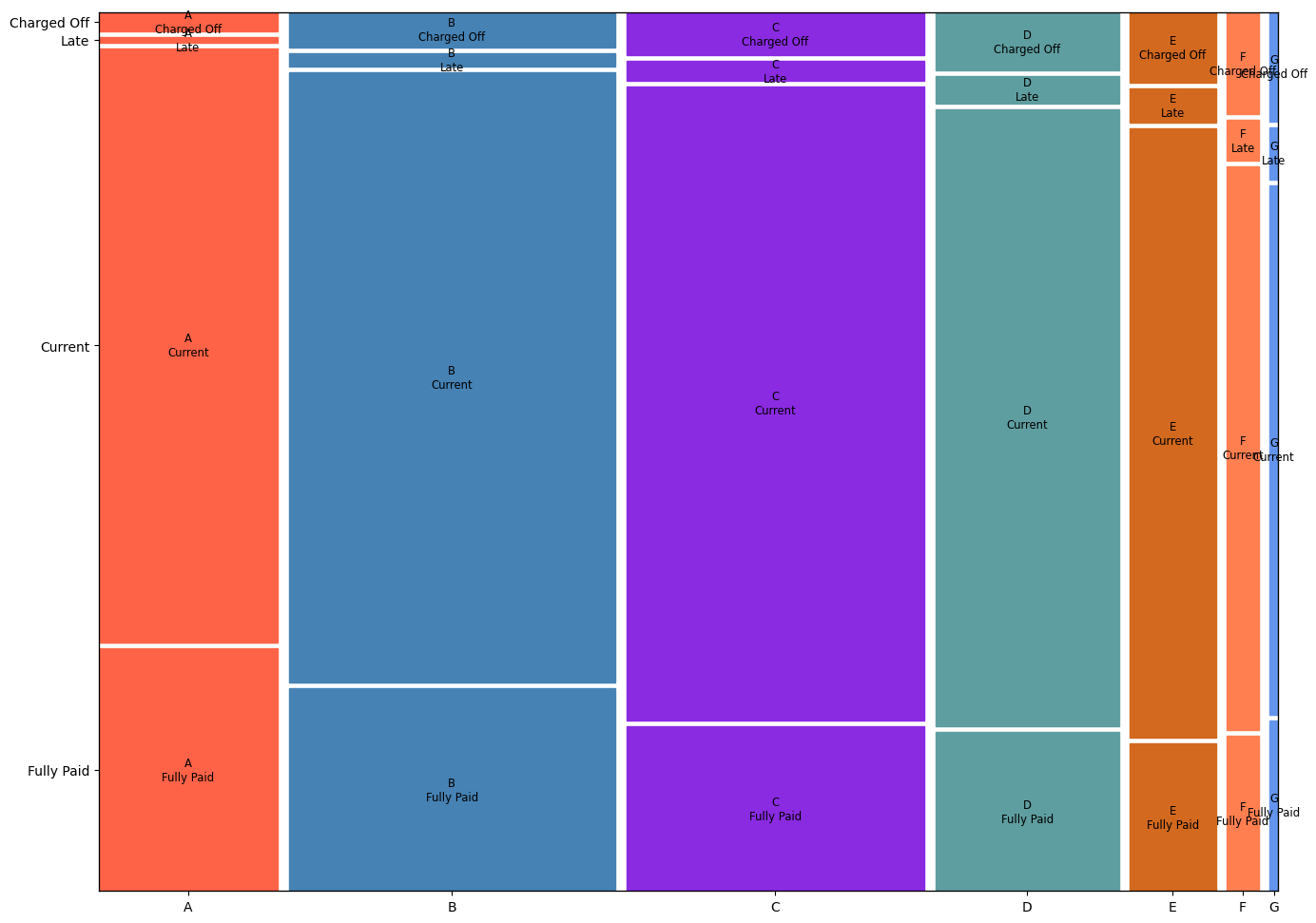
Mosaic Plot : 분할표에서 각 범주의 비율을 상자의 너비와 높이로 나타낸 그래프
Sourse
- https://thirdspacelearning.com/gcse-maths/statistics/frequency-table/
- https://www.jaspersoft.com/articles/what-is-a-bar-chart
- https://proclusacademy.com/blog/customize_matplotlib_piechart/
- https://www.questionpro.com/cross-tabulation.html