Supervised Model Selection
Based on the lecture “Intro. to Machine Learning (2023-2)” by Prof. Je Hyuk Lee, Dept. of Data Science, The Grad. School, Kookmin Univ.
Classification Metrics
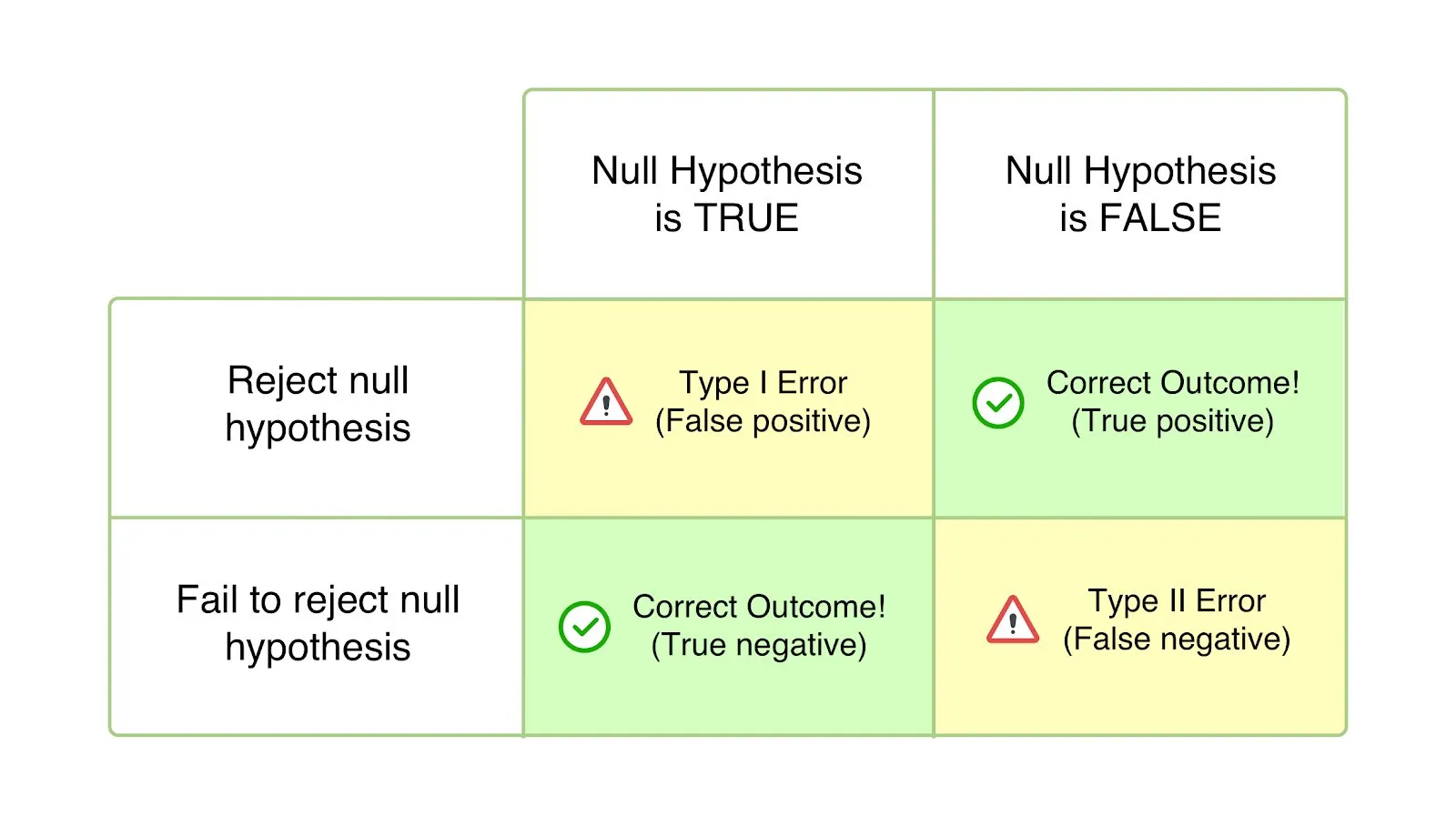
Confusion Matrix
TP(True Positive) : 긍정으로 예측한 것(Possitive) 중 옳게 예측한(True) 항목TN(True Negative) : 부정인 것(Negative) 중 옳게 예측한(True) 항목FP(False Possitive) : 긍정으로 예측한 것(Possitive) 중 잘못 예측한(False) 항목FN(False Negative) : 부정으로 예측한 것(Negative) 중 잘못 예측한(False) 항목
Sensitive to Threshold
-
정확도(Accuracy) : 전체 관측치 대비 옳게 예측한 관측치 비율
\[\frac{TP + TN}{TP + TN + FP + FN}\] -
민감도(Sensitivity) 혹은 재현율(Recall) : 실제 긍정인 관측치 대비 옳게 예측한 관측치 비율
\[\frac{TP}{TP + FN}\] -
특이도(Specificity) : 실제 부정인 관측치 대비 옳게 예측한 관측치 비율
\[\frac{TN}{TN + FP}\] -
정밀도(Precision) : 긍정으로 예측한 관측치 대비 옳게 예측한 관측치 비율
\[\frac{TP}{TP + FP}\] -
F1-Score : 재현율과 정밀도의 조화 평균
\[2 \times \frac{precision \times recall}{precision + recall}\]- 재현율 : 제1종 오류(참을 거짓으로 예측하는 오류;
FN)를 강조하는 지표 - 정밀도 : 제2종 오류(거짓을 참으로 예측하는 오류;
FP)를 강조하는 지표
- 재현율 : 제1종 오류(참을 거짓으로 예측하는 오류;
AUROC : Robust to Threshold
-
AUROC
-
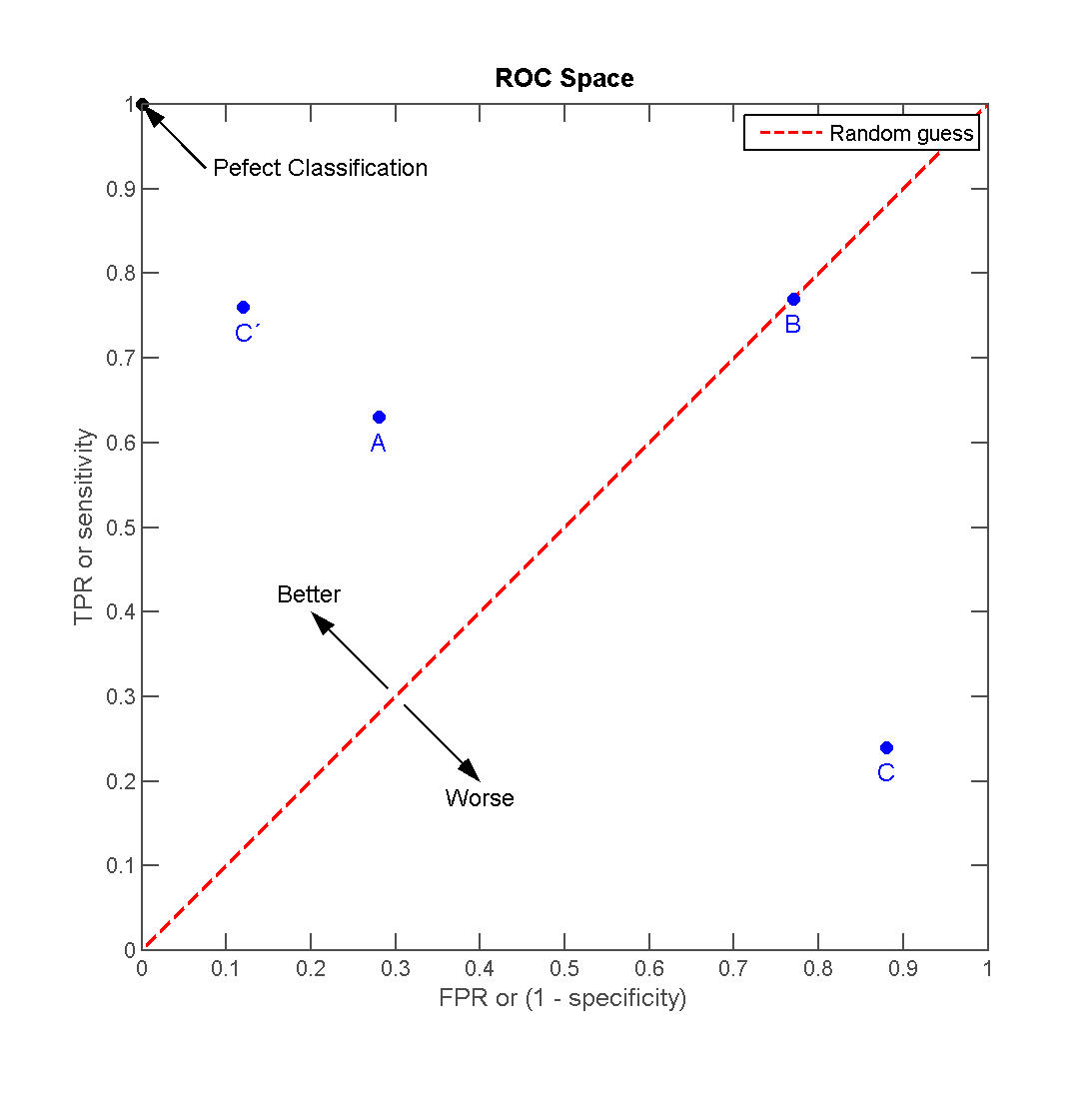
ROC Curve(Receiver Operating Characteristic Curve) : FPR 값에 따른 TPR의 변화 추이를 나타낸 곡선
-
AUROC(Area Under ROC) : ROC Curve 아래 면적
- 이상적 분류기(Ideal Classifier) : 1
- 무작위 분류기(Random Classifier) : 0.5
-
-
개념 설명
-
\[\begin{aligned} FNR &=\frac{FN}{TP+FN} \end{aligned}\]FNR(False Negative Rate) : 실제 긍정인 관측치(TP+FN) 대비 잘못 예측한 관측치(FN) 비율 -
\[\begin{aligned} TPR &=\frac{TP}{TP+FN}\\ &= 1-FNR \end{aligned}\]TPR(True Positive Rate) : 실제 긍정인 관측치(TP+FN) 대비 옳게 예측한 관측치(TP) 비율 -
\[\begin{aligned} FPR &=\frac{FP}{TN+FP} \end{aligned}\]FPR(False Possitive Rate) : 실제 부정인 관측치(TN+FP) 대비 잘못 예측한 관측치(FP) 비율 -
\[\begin{aligned} TNR &=\frac{TN}{TN+FP}\\ &= 1-FPR \end{aligned}\]TNR(True Negative Rate) : 실제 부정인 관측치(TN+FP) 대비 옳게 예측한 관측치(TN) 비율
-
Regression Metrics
-
Average Error(AE)
\[AE=\frac{1}{n}\sum_{i=1}^{n}{y_{i}-\hat{y}_{i}}\]- 정의 : 오차의 합계
- 한계점 : 오차의 방향에 따른 크기 상쇄 가능성
-
Mean Squared Error(MSE) : 오차 자승의 평균
\[MSE = \frac{1}{n}\sum_{i=1}^{n}{(y_{i}-\hat{y}_{i})^2}\] -
Root Mean Squared Error(RMSE) : 오차 자승의 평균의 자승근
\[RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}{(y_{i}-\hat{y}_{i})^2}}\] -
Mean Absolute Error(MAE) : 오차 절대값의 평균
\[MAE = \frac{1}{n}\sum_{i=1}^{n}{\vert y_{i}-\hat{y}_{i} \vert}\] -
Mean Absolute Percentage Error(MAPE) : 실제값 대비 오차 비율 절대값의 평균
\[MAPE = \frac{1}{n}\sum_{i=1}^{n}{\vert \frac{y_{i}-\hat{y}_{i}}{y_{i}} \vert}\]
Split
Generalization Problem
-
일반화(Generalization) : 모델링 목적으로서, 모델이 훈련 관측치에서 학습한 패턴을 사용하여 이전에 보지 못한 관측치에 대하여 예측하는 것
-
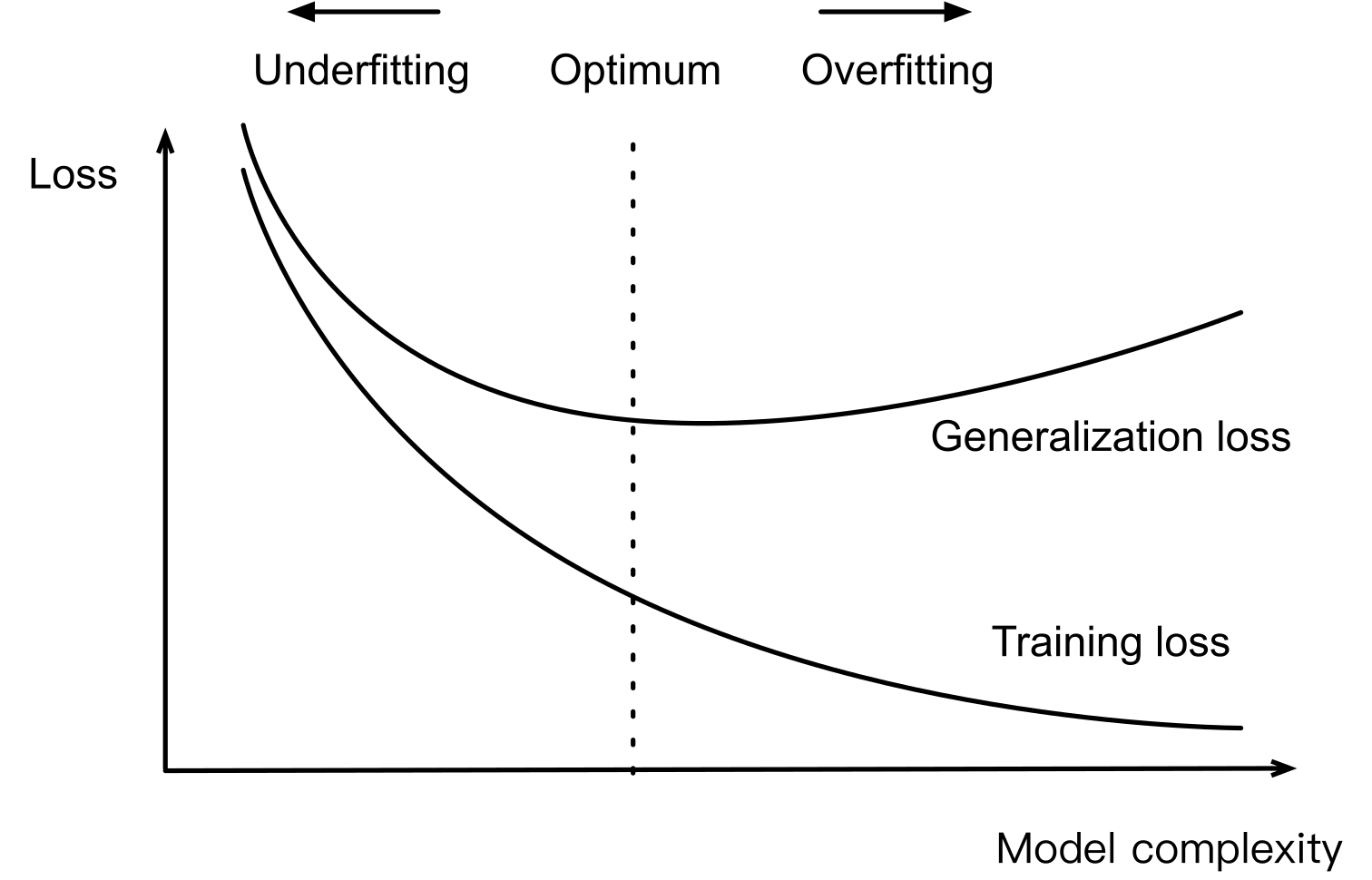
문제점 : 과적합 현상
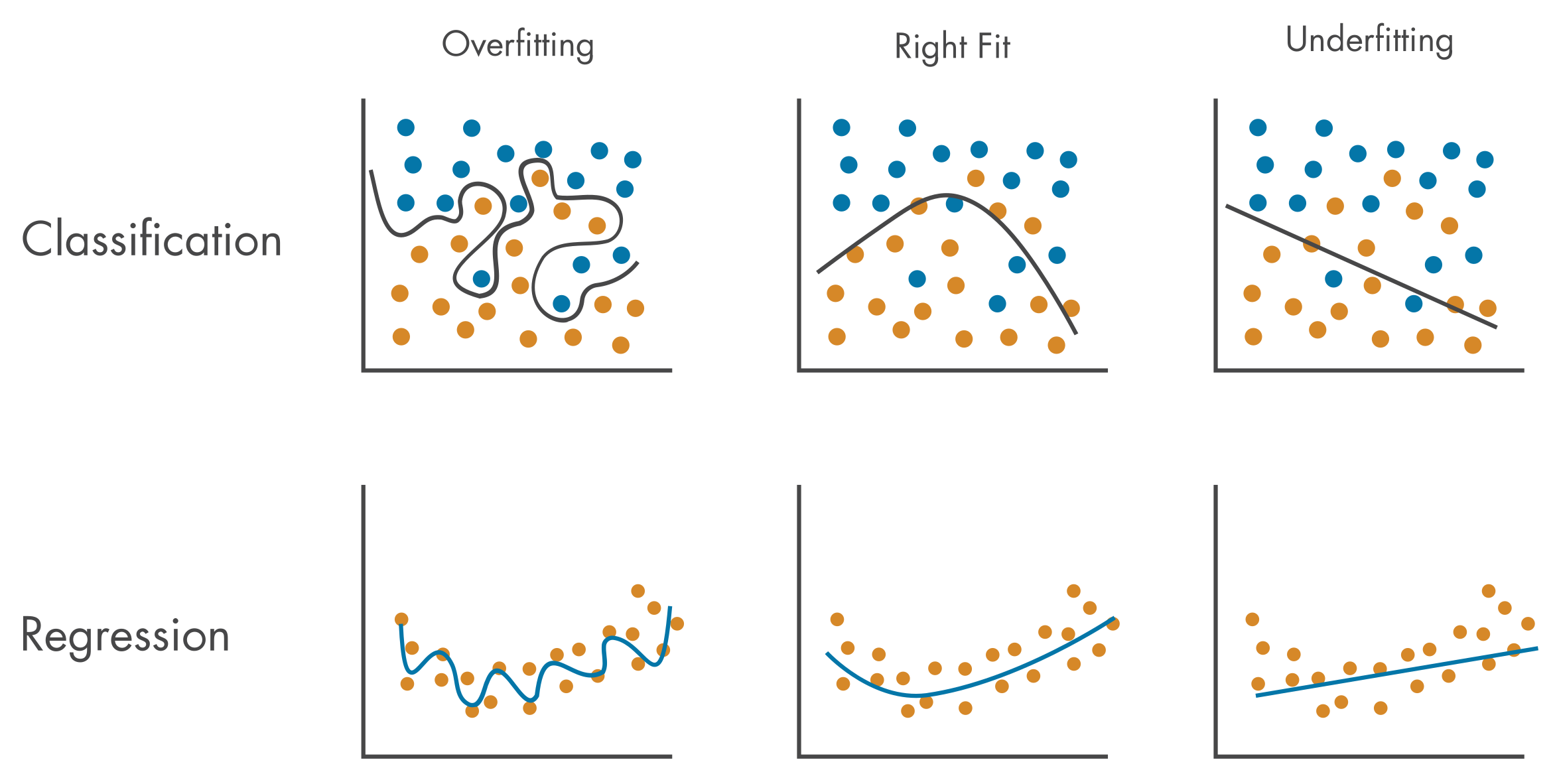
- 과대적합(Overfitting) : 모델이 일반적이지 않은, 즉 훈련 관측치에서만 포착되는 노이즈나 이상치까지 학습하여 신규 관측치에 대해서는 제대로 기능하지 못하는 상태
- 과소적합(Underfitting) : 모델이 훈련 관측치에서 나타나는 일반적인 패턴을 충분히 학습하지 못하여 관측치의 다양성과 복잡성을 잡아내지 못하는 상태
-
해결 방법 : $E_{gen}$ 최소화
-
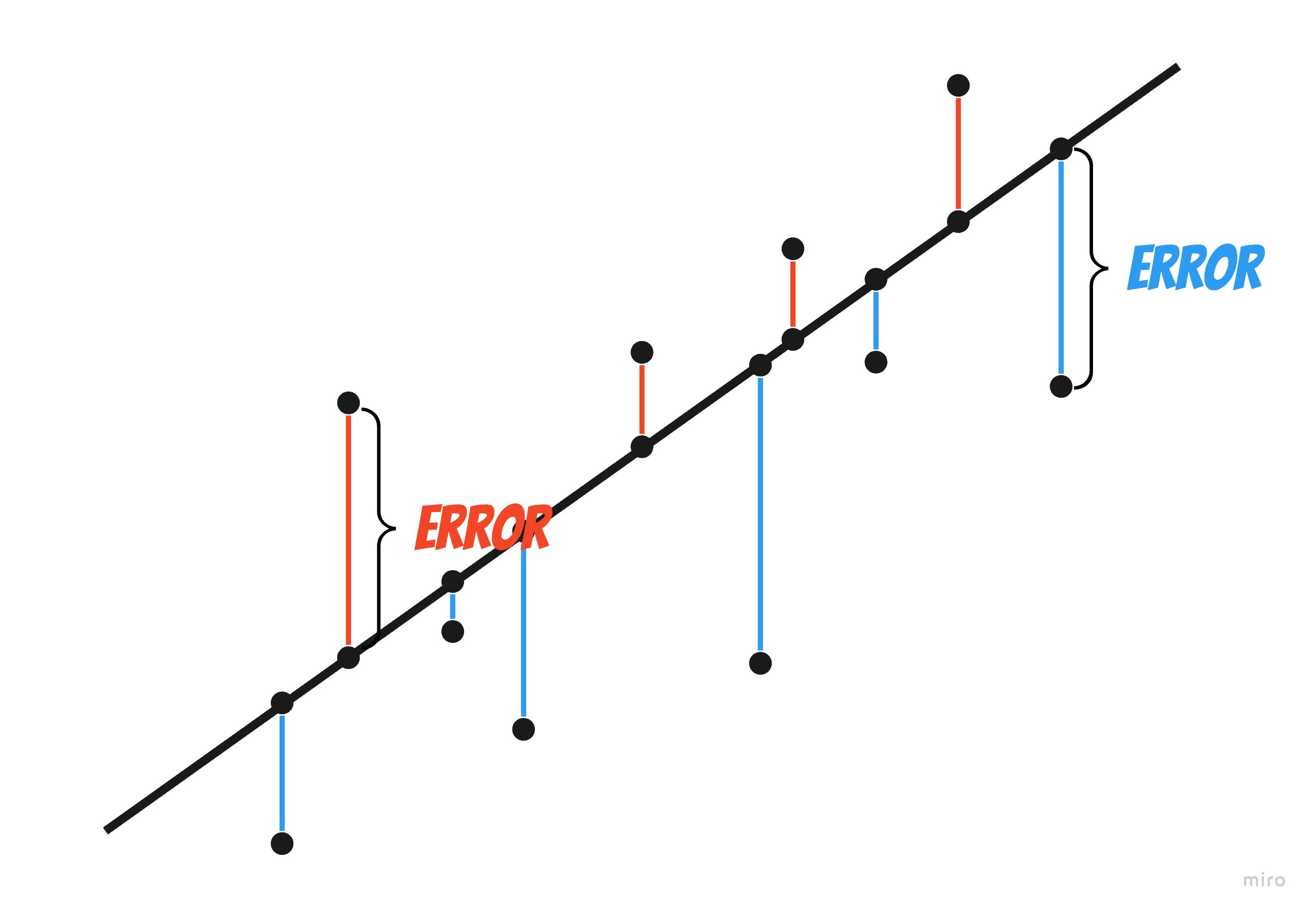
Training Error : Training Data Set 에 대한 오차
\[E_{trn} = \sum^{N_{trn}}_{i=1}{L(y_{i},\hat{y}_{i})}\] -
Generalization Error : Unseen Data Set 에 대한 오차
\[E_{gen}=\int{L(y_{i},\hat{y}_{i})}\]
-
Estimation
- $E_{gen}$ 측정 상의 문제점
- Unseen Data Set 자체에 대해서 알 수 없으므로 이상적인 개념임
- 해당 모수를 추정하기 위하여 추정량 $E_{val}$, $E_{tst}$ 를 제시함
-
Split Seen Data Set
Training: 모델 훈련 시 사용하는 표본으로서, 해당 표본으로부터 $E_{val}$ 을 추정함Validation: 모델 간 성능 비교 시 사용하는 표본으로서, 해당 표본으로부터 $E_{tst}$ 를 추정함Test: 최종 선택된 모델 성능 측정 시 사용하는 표본으로서, 해당 표본로부터 $E_{gen}$ 를 추정함
Cross Validation
-
교차 검증(Cross Validation)
- 정의 : 표본을 여러 세트로 나누어 모델을 여러 번 학습하고 평가함으로써 모델의 일반화 성능을 측정하는 절차
- 필요성 :
Training에서Test를 분리한 상태에서Validation을 재차 분리하기에는 학습에 사용할 표본 크기가 충분하지 않음
-
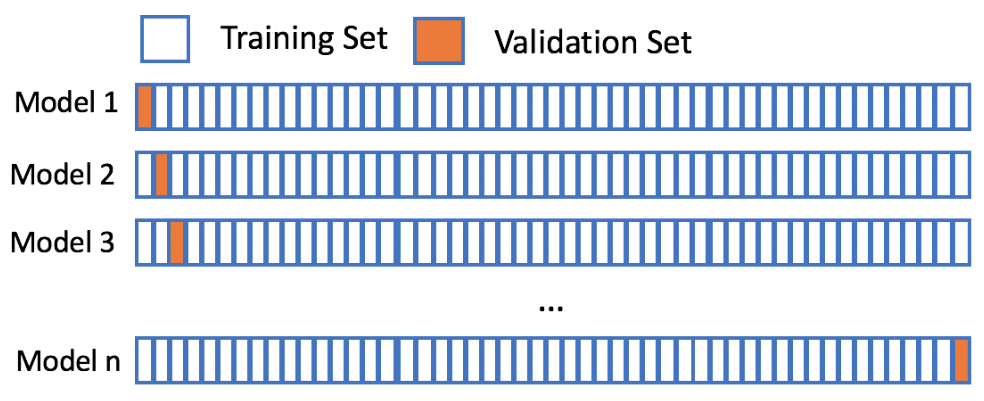
LOOCV(Leave-One-Out Cross Validation)
- $n$ 개의 표본을 $n-1$ 개의
training과 $1$ 개의validation으로 나누어 $n$ 번 학습하는 방식
- $n$ 개의 표본을 $n-1$ 개의
-
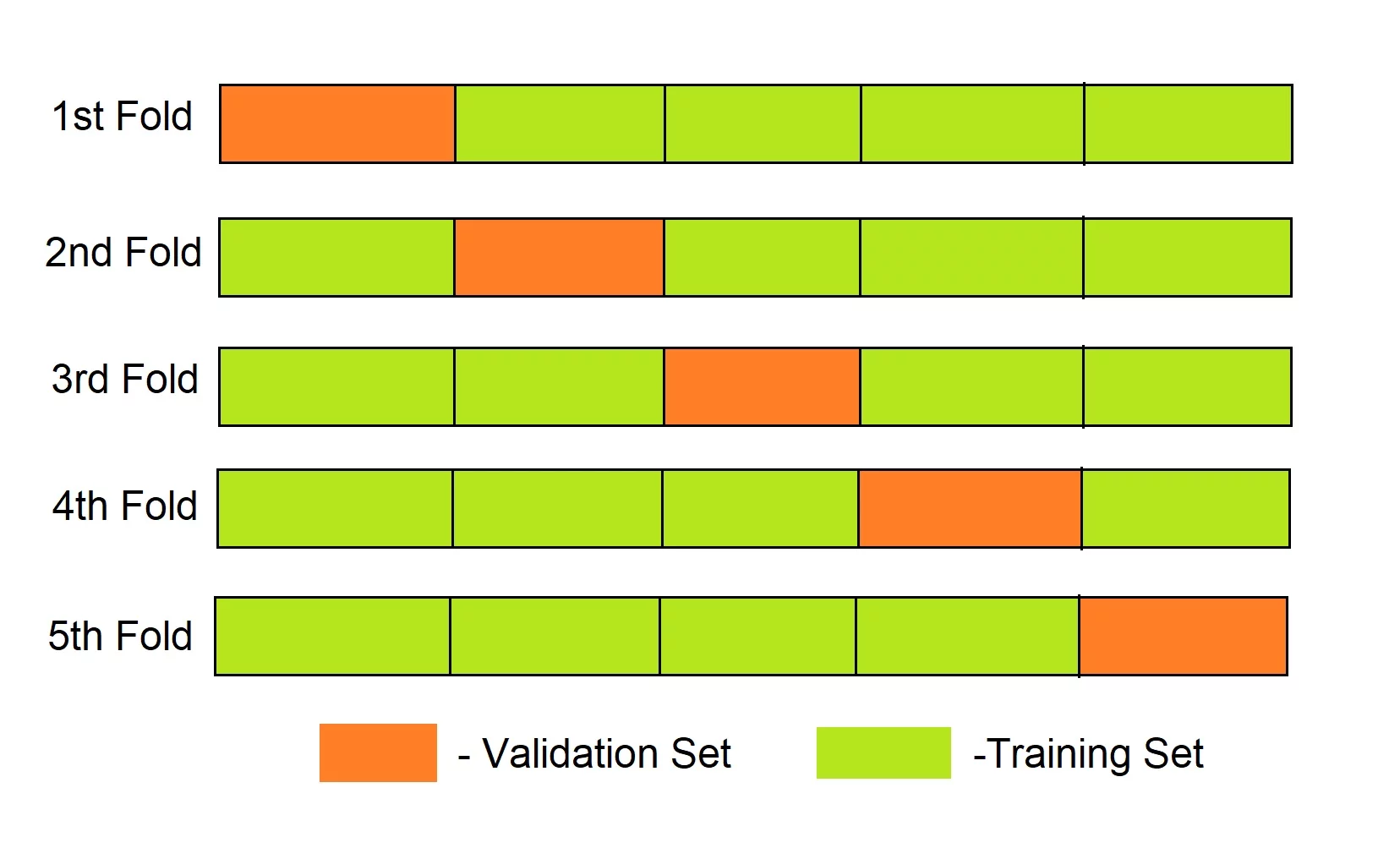
k-Fold Cross Validation
- $n$ 개의 표본을 $k$ 개의 데이터 세트로 나누고, $k-1$ 개는
training으로, $1$ 개는validation으로 구분하여 $k$ 번 학습하는 방식
- $n$ 개의 표본을 $k$ 개의 데이터 세트로 나누고, $k-1$ 개는