Taylor Series

• 극점(Extremum): 함수 $f:X \to Y$ 에 대하여 함수값 $y=f(x)$ 의 국소적인 최대 혹은 최소 지점

  

• 극대점(Local Maximum): 주위 모든 점의 함수값 이상의 함수값을 가지는 지점으로서, 함수 $f$ 가 구간 $[a,b]$ 에서 미분 가능하고, $x=c\in[a,b]$ 에서 극대값을 가지면 다음을 만족함

  \[\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x}f(x)\Big\vert_{x=c}=0, \quad \frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}f(x)\Big\vert_{x=c}<0 \end{aligned}\]

• 극소점(Local Minimum): 주위 모든 점의 함수값 이하의 함수값을 가지는 지점으로서, 함수 $f$ 가 구간 $[a,b]$ 에서 미분 가능하고, $x=c\in[a,b]$ 에서 극소값을 가지면 다음을 만족함

  \[\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x}f(x)\Big\vert_{x=c}=0, \quad \frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}f(x)\Big\vert_{x=c}>0 \end{aligned}\]

Taylor Polynomial

---

• 테일러 다항식(Taylor Polynomial) : $x=a$ 에서 미분 가능한 함수 $f:X \to Y$ 에 대하여, $f$ 와 $x=a$ 에서 근사하는 $n$ 차 함수

  \[\begin{aligned} f(x) \approx \sum_{k=0}^{n}{\frac{f^{k}(a)}{k!}(x-a)^{k}}, \quad f^{k}(a) = \frac{\mathrm{d}^{k}}{\mathrm{d}x^{k}}f(x)\Big\vert_{x=a} \end{aligned}\]

• 테일러 급수(Taylor Series) : $n \to \infty$ 인 경우의 테일러 다항식

  \[\begin{aligned} f(x) &\approx f(a) + f^{(1)}(a)(x-a) + \frac{f^{(2)}(a)}{2!}(x-a)^{2} + \cdots + \frac{f^{(k)}(a)}{k!}(x-a)^{k} + \cdots \end{aligned}\]

• 매클로린 급수(Maclaurin’s Series) : $a=0$ 인 경우의 테일러 급수

  \[\begin{aligned} f(x) &\approx f(0) + f^{(1)}(0)x + \frac{f^{(2)}(0)}{2!}x^{2} + \cdots + \frac{f^{(k)}(0)}{n!}x^{k} + \cdots \end{aligned}\]

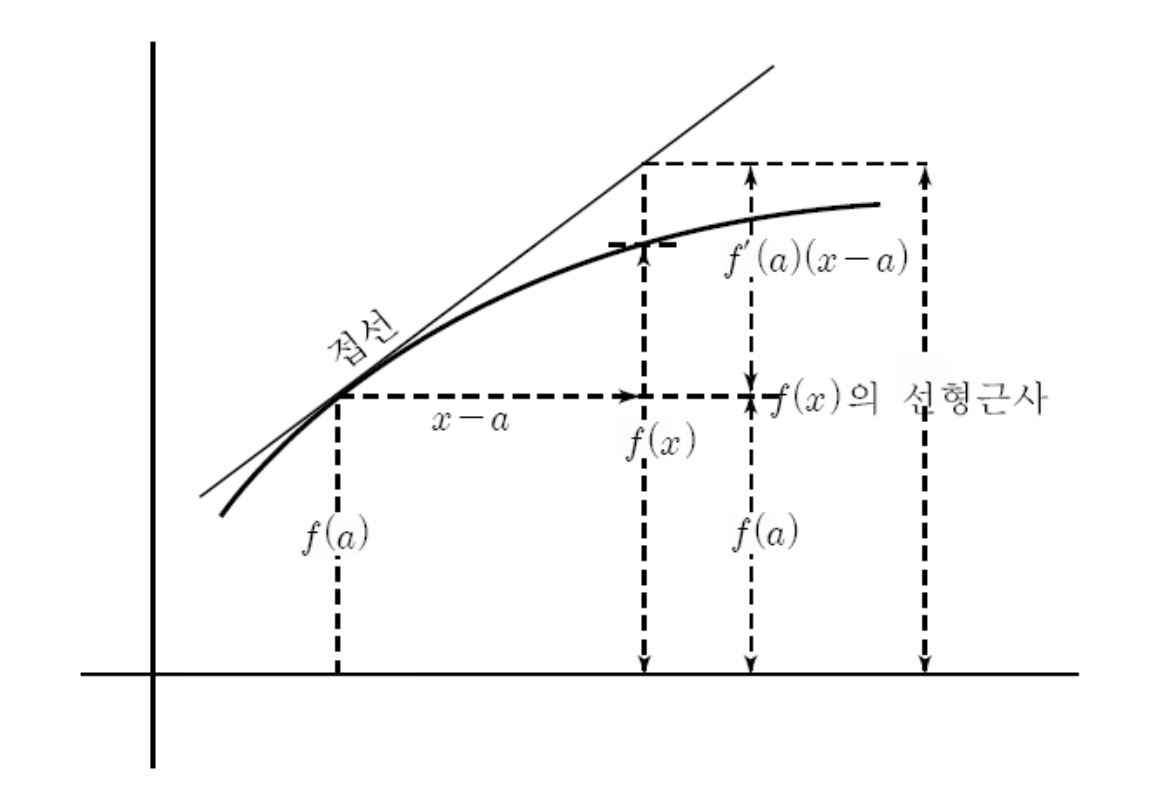
• 선형 근사(Linear Approximation) : $x=a$ 에서 $f: X \to Y$ 에 근사하는 $1$ 차 함수

  \[\begin{aligned} f(x) \approx f(a) + f^{\prime}(a)(x-a) \end{aligned}\]

Moment

---

• 적률(Moment): 확률변수 $X$ 의 $n$ 차 적률은 확률변수 $X^{n}$ 의 기대값임

  \[\begin{aligned} \mathbb{E}\left[X^{n}\right] &= \begin{cases} \sum_{x}{x^{n}f(x)}\\ \int_{-\infty}^{\infty}{x^{n}f(x)\text{d}x} \end{cases} \end{aligned}\]

  • 원점 적률(Origin Moment): 원점에 대한 적률로서 평균

    \[\begin{aligned} \mu^{\prime}_{n} &= \mathbb{E}\left[X^{n}\right] \end{aligned}\]

  • 중심 적률(Central Moment): 중심점(혹은 평균) $\mu$ 에 대한 적률로서 분산

    \[\begin{aligned} \mu_{n} &= \mathbb{E}\left[(X-\mu)^{n}\right] \end{aligned}\]

• 적률생성함수(Moment Generating Function): 특정 분포의 적률을 생성하는 함수

  \[\begin{aligned} M_{X}(t) = \mathbb{E}\left[e^{tX}\right] = \int_{-\infty}^{\infty}{e^{tX}f(x)\text{d}x} \end{aligned}\]

  • 적률생성함수의 매클로린 전개:

    \[\begin{aligned} \mathbb{E}\left[e^{tX}\right] \approx \mathbb{E}\left[\sum_{n=0}^{\infty}{\frac{t^{n}X^{n}}{n!}}\right] = \sum_{n=0}^{\infty}{\frac{t^{n}}{n!}\mathbb{E}\left[X^{n}\right]} \end{aligned}\]

  • 확률변수 $X$ 의 원점에 대한 $n$ 차 적률은 적률생성함수를 $t=0$ 에서 $t^{n}$ 에 대하여 미분한 값임:

    \[\begin{aligned} \mathbb{E}\left[X^{n}\right] &\approx \frac{\text{d}^{n}}{\text{d}t^{n}}M_{X}(t) \Big\vert_{t=0} \end{aligned}\]