Transformer

Attention is all you need

---

• 트랜스포머(Transformer) : 시계열 데이터를 순차 입력 받는 RNN 계열 레이어를 배제하고 어텐션 메커니즘을 전적으로 활용하여 시계열 데이터의 병렬 처리를 도모하는 기계 번역 아키텍처

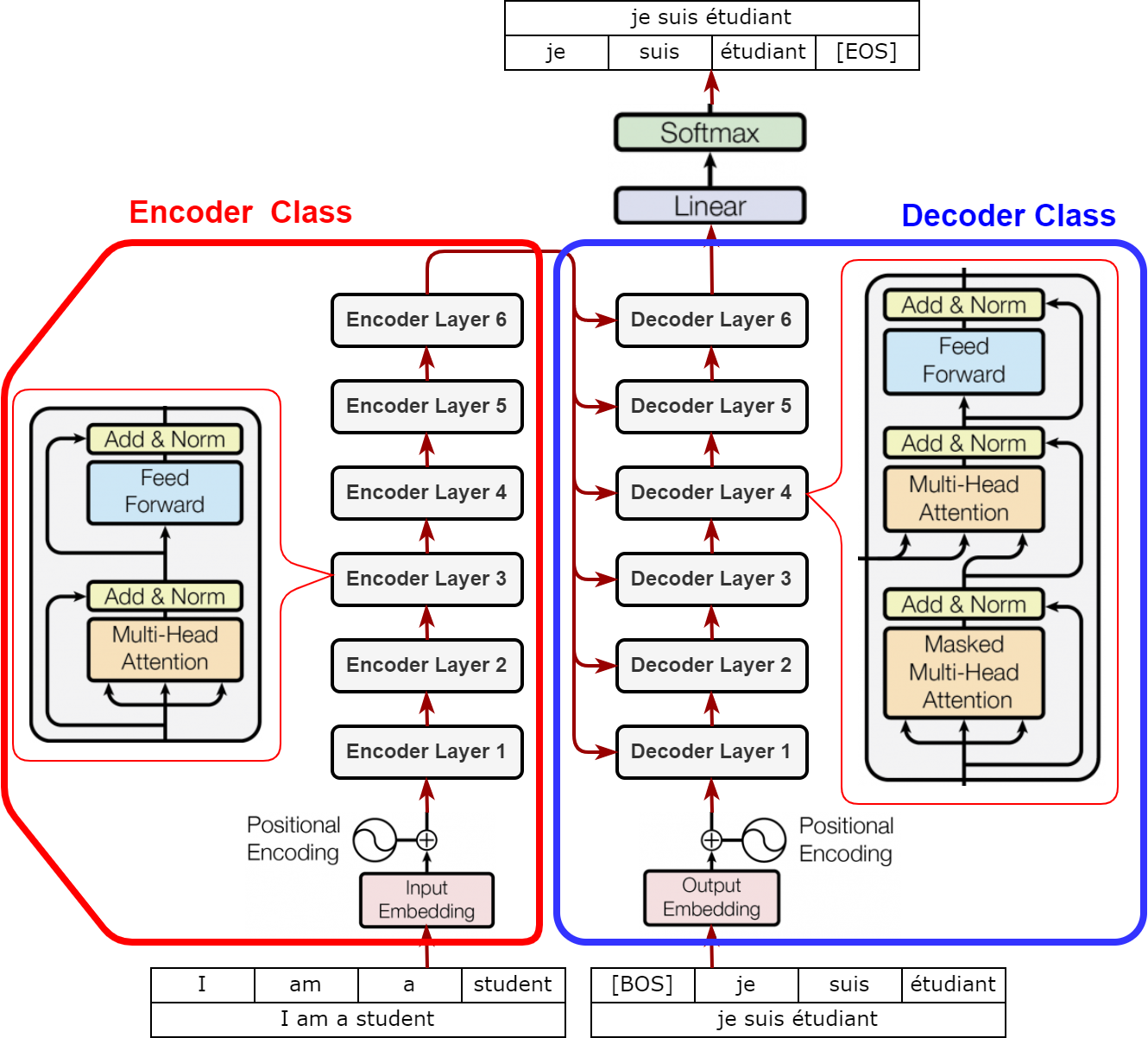
• TOTAL ARCHITECTURE : SEQ2SEQ 의 ENCODER-DECODER 구조를 따름

  

  • ENCODER : Natural Language Understanding & Feature Extraction
  • DECODER : Natural Language Generation

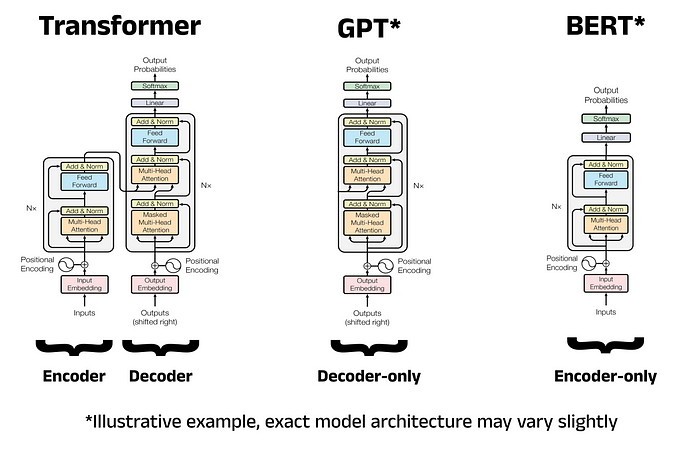
• Transformer Application

  

  • BERT(Bidirectional Encoder Representations from Transformers) : LLM, Transformer Encoder Application
  • GPT(Generative Pre-Training) : GM, Transformer Decoder Application

Core Techs

---

• Token Embedding : 입력 문장 내 단어들 각각의 정보를 표현하는 벡터를 생성함

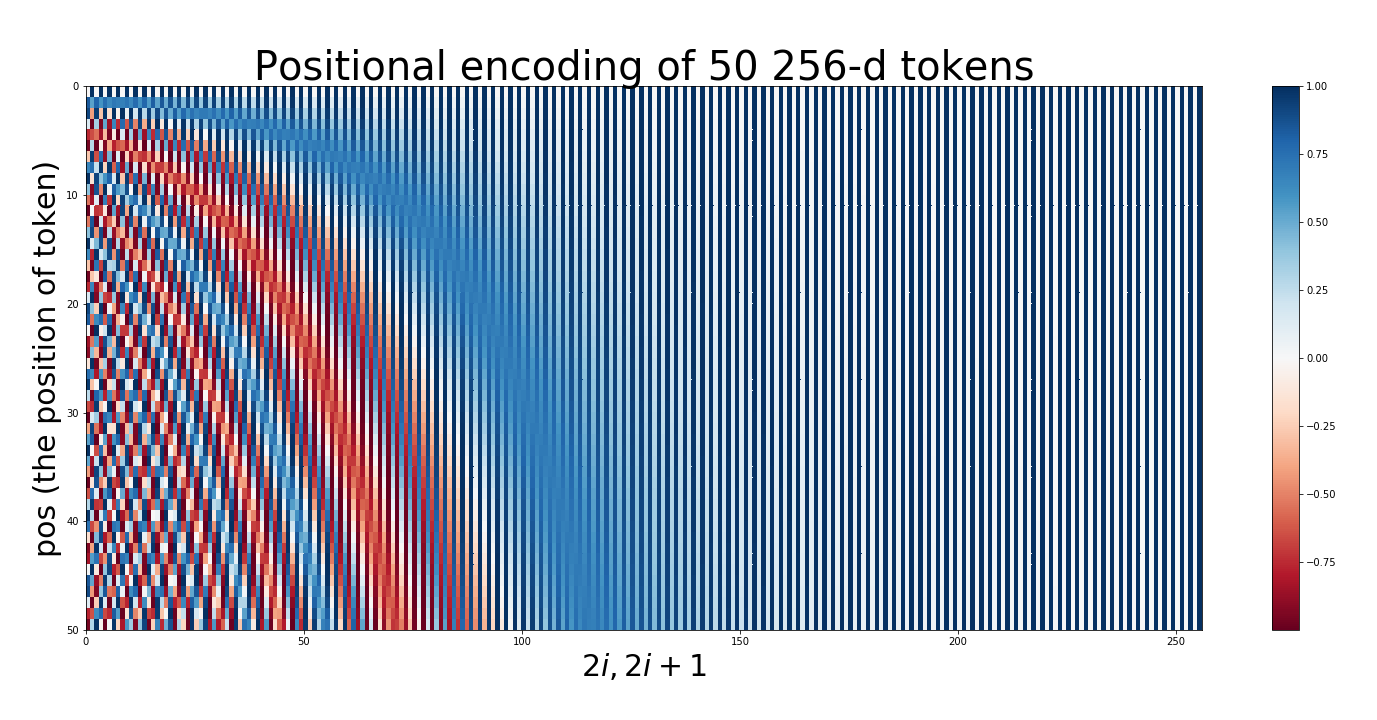
• Positional Encoding : 입력 문장 내 단어들의 위치 정보를 표현하는 벡터를 생성함

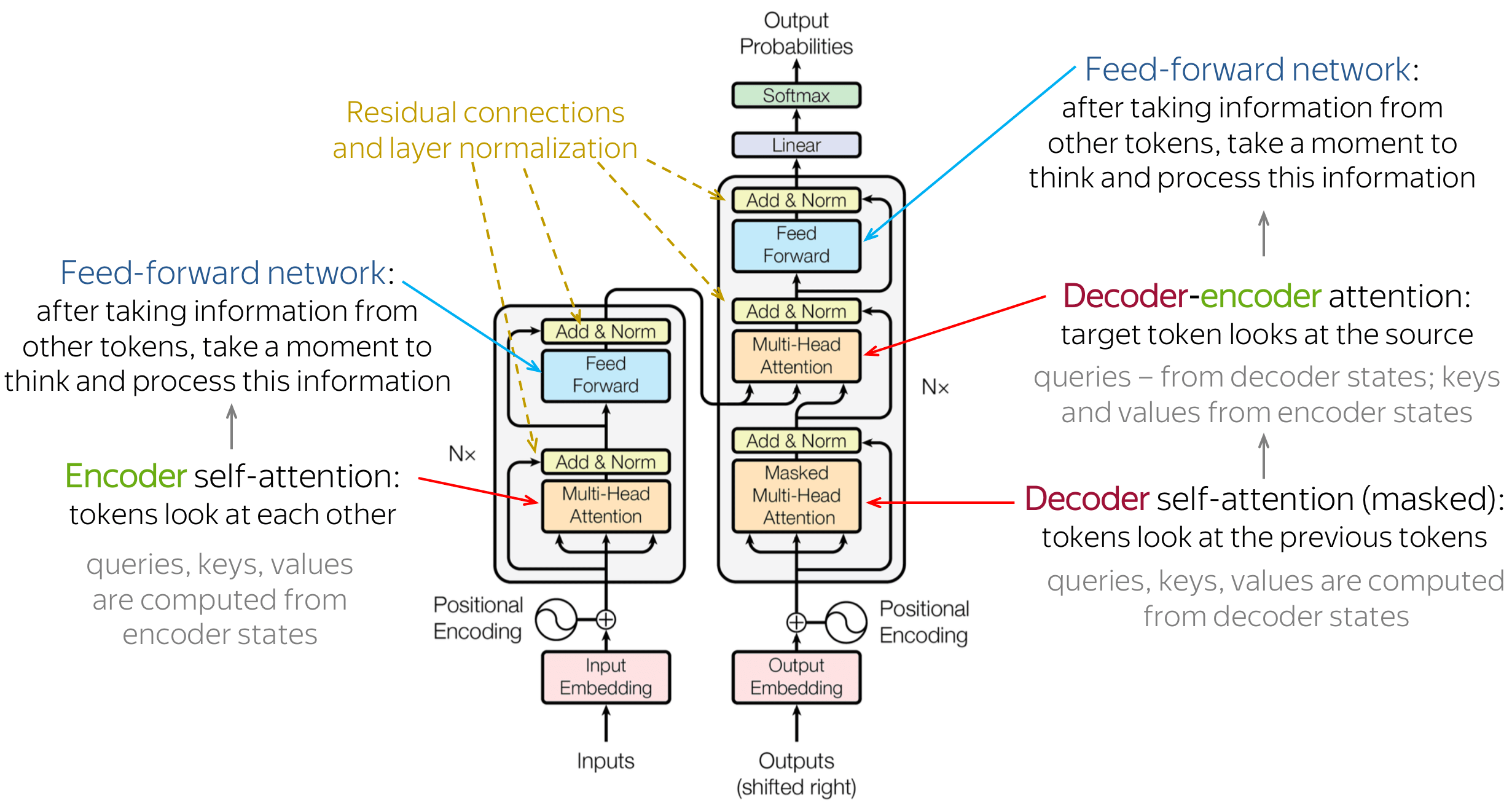
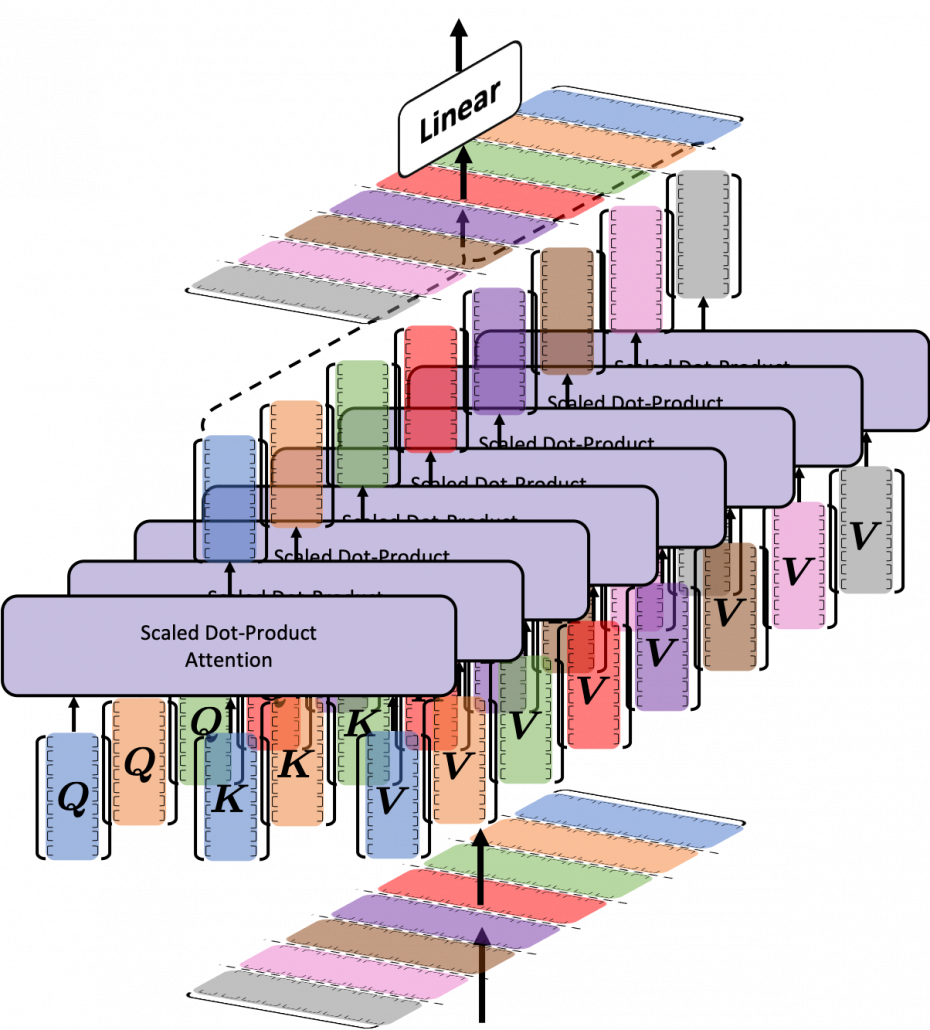
• Multi-Head Self Attention @ Encoder : 인코더에서 입력 문장 내 단어들 간 관계를 학습하여 각 단어가 문장에서 어떤 역할을 하는지를 반영하는 문맥 벡터를 생성함

• Multi-Head Masked Self Attention @ Decoder : 디코더에서 출력 문장 내 단어들 간 관계를 학습하여 각 단어의 문맥 벡터를 생성하되, 이전 순번까지의 단어만 참고하도록 마스킹하여 다음 순번에 관한 정보가 유출되는 것을 방지함

• Multi-Head Cross Attention @ Decoder : 출력 문장의 각 단어가 인코더의 출력들과 맺는 관계를 학습하여 출력 문장 생성 시 개별 순번마다 입력 문장에서 어떤 부분이 중요한지 반영하는 문맥 벡터를 생성함

Positional Encoding

---

Condition

• 주기성(Periodicity) : 벡터는 단어 간 상대적 위치를 표현할 수 있어야 함
  • 단어의 절대적 위치가 아니라 단어 간 상대적 위치에 따른 관계 패턴이 문장의 의미를 결정함
  • 어텐션 메커니즘은 각 단어가 서로를 참조하는 방식으로 정보를 처리함
  • 주기성을 띠는 함수가 관계 패턴을 결정짓는 상대적 위치를 표현하기에 효율적임
• 연속성(Continuity) : 벡터는 연속적인 값을 가져야 함
  • 임의의 두 단어 순번 간 거리가 일정하다면, 벡터 간 거리도 일정해야 함
  • 임의의 두 단어 순번 간 위치가 비슷하다면, 벡터 값도 유사해야 함
  • 불연속적인 값이 존재하면 모형이 상대적 위치에 따른 관계 패턴을 학습하기 어려움
• 일반화(Generalization) : 벡터는 특정 모형 구조나 훈련 데이터에 종속되지 않고, 모든 상황에서 일정한 방식으로 사용할 수 있어야 함
  • 벡터는 모형 설계 방식과 상관없이 일정한 방식으로 위치 정보를 제공해야 함
  • 벡터는 시퀀스 길이에 상관없이 일정한 정보 해상도를 가져야 함
• 단어 임베딩과의 균형(Balance with Word Embedding) : 벡터의 원소값은 단어의 의미 정보와 위치 정보가 균형을 이룰 수 있는 범위 내에 존재해야 함
  • 원소값이 너무 크면 단어의 의미가 왜곡될 수 있음
  • 원소값이 너무 작으면 위치 정보가 무시될 수 있음

Positional Encoding

\[\begin{aligned} \overrightarrow{\mathbf{e}}_{\text{POS}} &=\begin{pmatrix} \sin{\frac{POS}{10000^{0}}} \\ \cos{\frac{POS}{10000^{0}}} \\ \sin{\frac{POS}{10000^{2/8}}} \\ \cos{\frac{POS}{10000^{2/8}}} \\ \sin{\frac{POS}{10000^{4/8}}} \\ \cos{\frac{POS}{10000^{4/8}}} \\ \sin{\frac{POS}{10000^{6/8}}} \\ \cos{\frac{POS}{10000^{6/8}}} \end{pmatrix}, \quad \text{where} \quad d=8 \end{aligned}\]

• FUNCTION

  

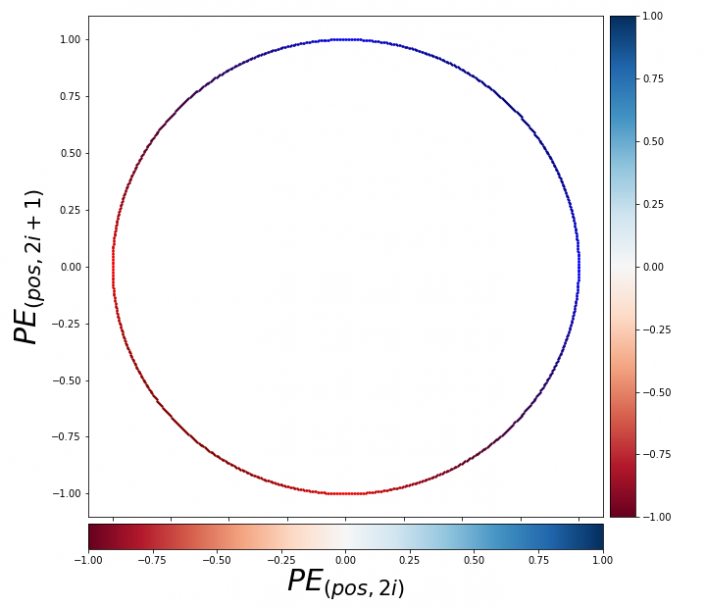
  \[\begin{aligned} PE(POS,2i)&=\sin{\frac{POS}{10000^{2i/d}}}\\ PE(POS,2i+1)&=\cos{\frac{POS}{10000^{2i/d}}} \end{aligned}\]
  • $POS$ : 문장 내 단어 순번
  • $d$ : 단어 임베딩 벡터 차원
  • $i=0,1,\cdots,\displaystyle\frac{d}{2}-1$ : 포지셔널 인코딩 벡터의 차원 인덱스

• PERIODICITY : 포지셔널 인코딩 벡터는 위치 간 관계(혹은 위치의 변화)를 부드러운(연속적인) 회전 변환 형태로 표현함

  

  \[\begin{aligned} \begin{pmatrix}\sin{\frac{POS+K}{10000^{2i/d}}} \\ \cos{\frac{POS+K}{10000^{2i/d}}}\end{pmatrix} = \begin{pmatrix}\cos{\frac{K}{10000^{2i/d}}} & \sin{\frac{K}{10000^{2i/d}}} \\ -\sin{\frac{K}{10000^{2i/d}}} & \cos{\frac{K}{10000^{2i/d}}}\end{pmatrix} \cdot \begin{pmatrix}\sin{\frac{POS}{10000^{2i/d}}} \\ \cos{\frac{POS}{10000^{2i/d}}}\end{pmatrix} \end{aligned}\]
  • \(\displaystyle\begin{pmatrix}\cos{\frac{K}{10000^{2i/d}}} & \sin{\frac{K}{10000^{2i/d}}} \\ -\sin{\frac{K}{10000^{2i/d}}} & \cos{\frac{K}{10000^{2i/d}}}\end{pmatrix}\) : $2 \times 2$ Rotation Matrix
  • 즉, 임베딩 차원 $d=2$ 일 때, 위치가 $K$ 만큼 이동하게 되면 벡터 공간 상에서 특정한 크기 \(\displaystyle\frac{K}{10000^{2i/d}}\) 만큼의 회전 변환이 이루어짐

Single Layers

---

Encoder Layer

\[\begin{aligned} \mathbf{X}^{(0)} &=\text{Token-Embedding}\left(\text{Tokens}\right) + \text{Positional-Encoding}\left(\text{Tokens}\right)\\ \mathbf{H}^{(k)} &=\text{Layer-Norm}\Big[\text{Multi-Head}\left(\mathbf{X}^{(k)}\right) + \mathbf{X}^{(k)}\Big]\\ \mathbf{Y}^{(k)} &=\text{Layer-Norm}\Big[\text{FFN}\left(\mathbf{H}^{(k)}\right) + \mathbf{H}^{(k)}\Big] \end{aligned}\]

• $\mathbf{X}$ is Input Data of Single Layer, $\mathbf{Y}$ is Output Data of Single Layer
  • \(\mathbf{X}^{(k+1)}=\mathbf{Y}^{(k)}\) : Input Data of $k+1$ Encoder Layer is Output Data of $k$
  • Input Data of Initial Layer \(\mathbf{X}^{(0)}\) is Sum of Token Embedding & Positional Encoding Vector
  • Output Data of Final Layer \(\mathbf{Z}=\mathbf{Y}^{(K)}\) is Output of Encoder Module

• \(\text{Multi-Head}\left(\mathbf{X}^{(k)}\right)\) : Multi-Head Self Attention @ Encoder

• \(\text{FFN}\left(\mathbf{H}^{(k)}\right)\) : Feed-Forward Networks @ Encoder

  \[\begin{aligned} \text{FFN}\left(\mathbf{H}^{(k)}\right) &=\mathbf{W}^{(k)}_{2} \cdot \left(\text{ReLU}\left[\mathbf{W}^{(k)}_{1} \cdot \mathbf{H}^{(k)} + \overrightarrow{\mathbf{b}}^{(k)}_{1}\right]\right) + \overrightarrow{\mathbf{b}}^{(k)}_{2} \end{aligned}\]
  • $\mathbf{W}^{(k)}_{1} \in \mathbb{R}^{M \times 4d}$ : Dimension Expansion to four times the Dimension of the Embedding Vector
  • $\mathbf{W}^{(k)}_{2} \in \mathbb{R}^{M \times d}$ : Dimension Reduction to Embedding Vector Dimension

Decoder Layer

\[\begin{aligned} \mathcal{X}^{(0)} &=\text{Token-Embedding}\left(\text{Tokens}\right) + \text{Positional-Encoding}\left(\text{Tokens}\right)\\ \mathcal{H}^{(k)}_{1} &=\text{Layer-Norm}\Big[\text{Multi-Head}\left(\mathcal{X}^{(k)};\mathcal{M}\right) + \mathcal{X}^{(k)}\Big]\\ \mathcal{H}^{(k)}_{2} &=\text{Layer-Norm}\Big[\text{Multi-Head}\left(\mathcal{H}^{(k)}_{1},\mathbf{Z},\mathbf{Z}\right) + \mathcal{H}^{(k)}_{1}\Big]\\ \mathcal{Y}^{(k)} &=\text{Layer-Norm}\Big[\text{FFN}\left(\mathcal{H}^{(k)}_{2}\right) + \mathcal{H}^{(k)}_{2}\Big] \end{aligned}\]

• $\mathcal{X}$ is Input Data of Single Layer, $\mathcal{Y}$ is Output Data of Single Layer
  • \(\mathcal{X}^{(k+1)}=\mathcal{Y}^{(k)}\) : Input Data of $k+1$ Encoder Layer is Output Data of $k$
  • Input Data of Initial Layer \(\mathcal{X}^{(0)}\) is Sum of Token Embedding & Positional Encoding Vector
  • Output Data of Final Layer \(\mathcal{Z}=\mathcal{Y}^{(K)}\) is Output of Decoder Module

• \(\text{Multi-Head}\left(\mathcal{X}^{(k)};\mathcal{M}\right)\) : Multi-Head Masked Self Attention @ Decoder

  • $\mathcal{M}$ : Causal Mask(Upper-triangular mask)

• \(\text{Multi-Head}\left(\mathcal{H}^{(k)}_{1},\mathbf{Z},\mathbf{Z}\right)\) : Multi-Head Cross Attention @ Decoder

  • \(\mathbf{Z}\) : Output of Encoder Module

• \(\text{FFN}\left(\mathcal{H}^{(k)}_{2}\right)\) : Feed-Forward Networks @ Decoder

  \[\begin{aligned} \text{FFN}\left(\mathcal{H}^{(k)}_{2}\right) &=\mathbf{W}^{(k)}_{2} \cdot \left(\text{ReLU}\left[\mathbf{W}^{(k)}_{1} \cdot \mathcal{H}^{(k)}_{2} + \overrightarrow{\mathbf{b}}^{(k)}_{1}\right]\right) + \overrightarrow{\mathbf{b}}^{(k)}_{2} \end{aligned}\]
  • $\mathbf{W}^{(k)}_{1} \in \mathbb{R}^{M \times 4d}$ : Dimension Expansion to four times the Dimension of the Embedding Vector
  • $\mathbf{W}^{(k)}_{2} \in \mathbb{R}^{M \times d}$ : Dimension Reduction to Embedding Vector Dimension

---

Reference

• https://zeuskwon-ds.tistory.com/88
• https://bongholee.com/transformer-yoyag-jeongri-2/
• https://wikidocs.net/162096